Giải bài 9.12 trang 66 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

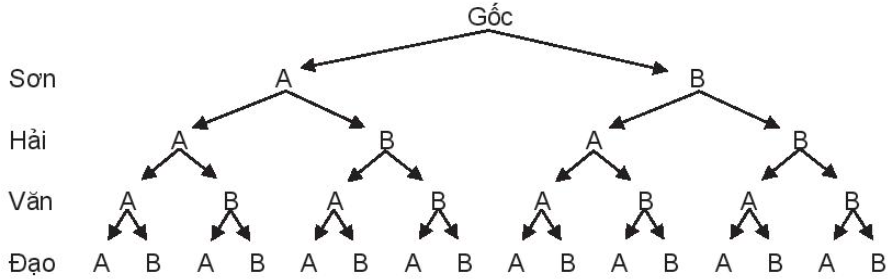
Đề bài

Trên một phố có hai quán ăn A, B. Bốn bạn Sơn, Hải, Văn, Đạo mỗi người chọn ngẫu nhiên một quán ăn.

a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.

b) Tính xác suất để:

• Tất cả đều vào một quán;

• Mỗi quán có đúng 2 bạn vào;

• Quán A có 3 bạn vào, quán B có 1 bạn vào

• Một quán có 3 bạn vào, quán kia có 1 bạn vào.

Lời giải chi tiết

a) Sơ đồ cây

b) Ta có \(\Omega  = \left\{ \begin{array}{l}AAAA;AAAB;AABA;AABB;ABAA;ABAB;ABBA;ABBB;\\BAAA;BAAB;BABA;BABB;BBAA;BBAB;BBBA;BBBB\end{array} \right\}\) .

Suy ra \(n\left( \Omega  \right) = 16\).

+ Gọi \(E\) là biến cố \(E\): “Tất cả đều vào một quán”. \(E = \left\{ {AAAA,BBBB} \right\}\). Suy ra \(n\left( E \right) = 2 \Rightarrow P\left( E \right) = \frac{2}{{16}} = \frac{1}{8}\).

+ Gọi \(F\) là biến cố \(F\): “Mỗi quán có đúng hai bạn vào”. \(F = \left\{ {AABB,ABAB,ABBA,BAAB,BABA,BBAA} \right\}\). Suy ra \(n\left( F \right) = 6 \Rightarrow P\left( F \right) = \frac{6}{{16}} = \frac{3}{8}\).

+ Gọi \(G\) là biến cố \(G\): “Quán A có ba bạn vào, quán B có một bạn vào”.

\(G = \left\{ {AAAB;AABA;ABAA;BAAA} \right\}\). Suy ra \(n\left( G \right) = 4 \Rightarrow P\left( G \right) = \frac{4}{{16}} = \frac{1}{4}\).

+ Gọi K là biến cố K: “Một quán có ba bạn vào, quán kia có một bạn vào”.

Khi đó \(P\left( K \right) = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}\).