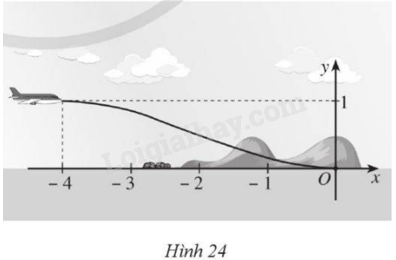
Giải bài 82 trang 38 sách bài tập toán 12 - Cánh diều

Đề bài

Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó khi gắn với hệ trục toạ độ \(Oxy\) được mô phỏng ở Hình 24. Biết đường bay của nó có dạng đồ thị hàm số bậc ba; vị trí bắt đầu hạ cánh có toạ độ \(\left( { - 4;1} \right)\) là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí gốc toạ độ là điểm cực tiểu của đồ thị hàm số.

a) Tìm công thức xác định hàm số mô phỏng đường bay của máy bay trên đoạn \(\left[ { - 4;0} \right]\).

b) Khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất bao nhiêu dặm? (Biết đơn vị trên hệ trục toạ độ là dặm).

c) Khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang bao nhiều dặm?

Lời giải chi tiết

a) Giả sử đường bay của máy bay có dạng là đồ thị của hàm số \(y = a{x^3} + b{{\rm{x}}^2} + c{\rm{x}} + d\) \(\left( {a \ne 0} \right)\) trên đoạn \(\left[ { - 4;0} \right]\).

\(y' = 3a{x^2} + 2b{\rm{x}} + c\)

Đồ thị hàm số đi qua điểm \(\left( {0;0} \right)\) nên ta có: \(a{.0^3} + b{.0^2} + c.0 + d = 0 \Leftrightarrow d = 0\)

\(x = 0\) là điểm cực tiểu của đồ thị hàm số nên ta có:

\(3a{.0^2} + 2b.0 + c = 0 \Leftrightarrow c = 0\).

Đồ thị hàm số đi qua điểm \(\left( { - 4;1} \right)\) nên ta có:

\(a.{\left( { - 4} \right)^3} + b.{\left( { - 4} \right)^2} + 0.\left( { - 4} \right) + 0 = 1 \Leftrightarrow  - 64a + 16b = 1\).

\(x =  - 4\) là điểm cực đại của đồ thị hàm số nên ta có:

\(3a.{\left( { - 4} \right)^2} + 2b.\left( { - 4} \right) = 0 \Leftrightarrow 48a - 8b = 0\).

Từ đó ta có \(a = \frac{1}{{32}},b = \frac{3}{{16}},c = 0\).

Vậy hàm số cần tìm là: \(y = \frac{1}{{32}}{x^3} + \frac{3}{{16}}{{\rm{x}}^2}\).

b) Thay \(x =  - 3\), ta được: \(y = \frac{1}{{32}}.{\left( { - 3} \right)^3} + \frac{3}{{16}}.{\left( { - 3} \right)^2} = \frac{{27}}{{32}}\).

Vậy khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay cách mặt đất \(\frac{{27}}{{32}} = 0,84375\) (dặm).

c) Thay \(y = 0,5\) ta được \(\frac{1}{{32}}{x^3} + \frac{3}{{16}}{{\rm{x}}^2} = 0,5 \Leftrightarrow x =  - 2 - 2\sqrt 3 ,x =  - 2 + 2\sqrt 3 ,x =  - 2\).

Do \(x \in \left[ { - 4;0} \right]\) nên \(x =  - 2\).

Vậy khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang 2 dặm.