Giải bài 8 trang 37 Chuyên đề học tập Toán 12 - Cánh diềuMột doanh nghiệp dự định sản xuất các hộp dựng nước giải khát có dạng hình trụ với dung tích là 500 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\) (Hình 5). Hãy tính bán kính đáy và chiều cao của chiếc hộp để diện tích vỏ hộp là nhỏ nhất (Hình 6). Quảng cáo
Đề bài Một doanh nghiệp dự định sản xuất các hộp dựng nước giải khát có dạng hình trụ với dung tích là 500 \({\rm{c}}{{\rm{m}}^{\rm{3}}}\) (Hình 5). Hãy tính bán kính đáy và chiều cao của chiếc hộp để diện tích vỏ hộp là nhỏ nhất (Hình 6).
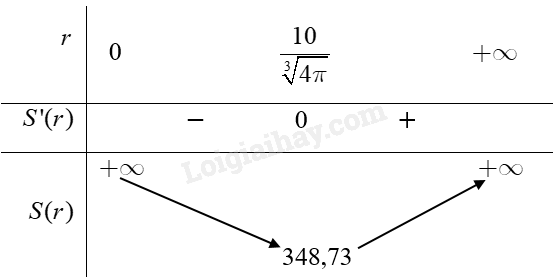
Phương pháp giải - Xem chi tiết +) Từ thể tích của hộp đựng nước giải khát ta sẽ biểu diễn được chiều cao của hộp nước theo bán kính đáy của nó \(h = \frac{{500}}{{\pi {r^2}}}\) +) Diện tích vỏ hộp chính là diện tích toàn phần của hộp nước hình trụ. +) Ta sẽ biểu diễn được diện tích vỏ hộp bằng một hàm số \(S(r)\)ẩn r +) Yêu cầu bài toán đồng nghĩa với việc ta phải đi tìm bán kính, chiều cao mà ở đó hàm số \(S(r)\)đạt giá trị nhỏ nhất. Lời giải chi tiết Chiều cao \(h\) của hộp đứng nước có dạng hình trụ là \(h = \frac{{500}}{{\pi {r^2}}}\) (cm). Diện tích mặt đáy của hộp đựng nước là \({S_{\rm{d}}} = \pi {r^2}\) (\({\rm{c}}{{\rm{m}}^{\rm{2}}}\)). Diện tích xung quanh của hộp đựng nước là \({S_{xq}} = 2\pi rh = 2\pi r.\frac{{500}}{{\pi {r^2}}} = \frac{{1000}}{r}{\rm{(c}}{{\rm{m}}^{\rm{2}}}{\rm{)}}\) Diện tích vỏ hộp là \(S = 2\pi {r^2} + \frac{{1000}}{r}({\rm{c}}{{\rm{m}}^{\rm{2}}})\). Xét hàm số \(S(r) = 2\pi {r^2} + \frac{{1000}}{r},r \in (0; + \infty ).\) Ta có \(S'(r) = 4\pi r - \frac{{1000}}{{{r^2}}}.\) Do đó \(S'(r) = 0 \Leftrightarrow r = \frac{{10}}{{\sqrt[3]{{4\pi }}}}.\) Ta có bảng biến thiên của hàm số \(S(r)\) như sau:
Căn cứ vào bảng biến thiên ta có \(\mathop {\min }\limits_{(0; + \infty )} S(r) \approx 348,73\) tại \(r = \frac{{10}}{{\sqrt[3]{{4\pi }}}}\) (cm). Vậy để diện tích vỏ hộp là nhỏ nhất thì bán kính của chiếc hộp là \(r = \frac{{10}}{{\sqrt[3]{{4\pi }}}}\) (cm) và chiều cao của chiếc hộp là \(h = \frac{{500}}{{\pi {{\left( {\frac{{10}}{{\sqrt[3]{{4\pi }}}}} \right)}^2}}} = \frac{{5{{\left( {\sqrt[3]{{4\pi }}} \right)}^2}}}{\pi }\) (cm).  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
