Giải bài 6 trang 36 Chuyên đề học tập Toán 12 - Cánh diềuMột nhà máy sản xuất một loại sản phẩm cho thị trường Mỹ. Biết rằng: - Chi phí cho các công việc hành chính chung của nhà máy là 90 đô la Mỹ (USD)/1 ngày. - Chi phí sản xuất là 0,09 USD/1 sản phẩm. - Các loại chi phí khác trong mỗi một ngày là \(\frac{{{x^2}}}{{10000}}\) (USD), trong đó \(x\) là số sản phẩm nhà máy sản xuất được trong ngày hôm đó. a) Tính tổng chi phí \(U(x)\) của mỗi một sản phẩm. b) Tìm \(x\) sao cho \(U(x)\) nhận giá trị nhỏ nhất. Quảng cáo
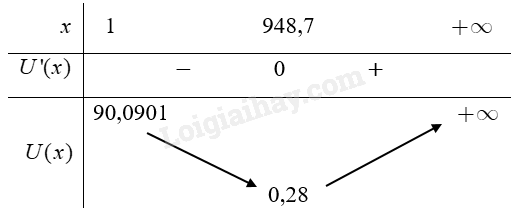
Đề bài Một nhà máy sản xuất một loại sản phẩm cho thị trường Mỹ. Biết rằng: - Chi phí cho các công việc hành chính chung của nhà máy là 90 đô la Mỹ (USD)/1 ngày. - Chi phí sản xuất là 0,09 USD/1 sản phẩm. - Các loại chi phí khác trong mỗi một ngày là \(\frac{{{x^2}}}{{10000}}\) (USD), trong đó \(x\) là số sản phẩm nhà máy sản xuất được trong ngày hôm đó. a) Tính tổng chi phí \(U(x)\) của mỗi một sản phẩm. b) Tìm \(x\) sao cho \(U(x)\) nhận giá trị nhỏ nhất. Phương pháp giải - Xem chi tiết +) Tìm biểu thức biểu diễn chi phí công việc hành chính một ngày cho một sản phẩm. +) Tìm biểu thức biểu diễn các loại chi phí khác cho một sản phẩm trong 1 ngày +) \(U(x)\) là tổng các chi phí trong 1 ngày của một sản phẩm. +) Ta sẽ đi tìm giá trị nhỏ nhất của hàm số \(U(x)\) trên \({\rm{[}}1; + \infty ).\) Lời giải chi tiết a) Chi phí cho các công việc hành chính chung trong một ngày của nhà máy cho mỗi sản phẩm là \(\frac{{90}}{x}\) (USD). Các loại chi phí khác trong một ngày của nhà máy cho mỗi sản phẩm là \(\frac{x}{{10000}}\) (USD). Tổng chi phí cho mỗi sản phẩm là \(U(x) = \frac{{90}}{x} + \frac{x}{{10000}}\) (USD). b) Xét hàm số \(U(x) = \frac{{90}}{x} + \frac{x}{{10000}}\) trên \({\rm{[}}1; + \infty ).\) Ta có \(U'(x) = - \frac{{90}}{{{x^2}}} + \frac{1}{{10000}}\). Do đó \(U'(x) = 0 \Leftrightarrow - \frac{{90}}{{{x^2}}} + \frac{1}{{10000}} = 0 \Leftrightarrow {x^2} = 900000 \Leftrightarrow x \approx 948,7\) (do \(x > 0\)). Bảng biến thiên hàm số:
Căn cứ vào bảng biến thiên hàm số ta có \(\mathop {\min }\limits_{{\rm{[}}1; + \infty )} U(x) \approx 0,28\) tại \(x \approx 948,7.\) Do \(x\) là số tự nhiên nên để chi phí nhỏ nhất khi \(x = 948\) hoặc \(x = 949.\) Ta có \(U(948) \approx 0,2797367089\) và \(U(949) \approx 0,2797366702\) nên \(U(948) > U(949)\). Vậy để \(U(x)\) nhận giá trị nhỏ nhất thì \(x = 949.\)  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
