Giải bài 8 trang 19 Chuyên đề học tập Toán 12 - Cánh diều

Đề bài

Giải sử một phòng thí nghiệm phải kiểm tra 120 mẫu máu người (mỗi mẫu của 1 người) để tìm ra các mẫu có chứa kháng thể \(X\). Giả sử xác suất để 1 mẫu máu có kháng thể \(X\) là 2% và các mẫu máu độc lập với nhau.

Do tính cấp bách của công tác phòng chống dịch nên thời gian dành cho xét nghiệm là rất ngắn. Thay vì xét nghiệm từng mẫu một, người ta làm như sau: Chia 120 mẫu thành 6 nhóm, mỗi nhóm có 20 mẫu. Lấy một ít máu từ mỗi mấu trong cùng một nhóm trộn với nhau để được 1 mẫu hỗn hợp rồi xét nghiệm mẫu hỗn hợp đó. Nếu kết quả xét nghiệm mẫu hỗn hợp là âm tính (mẫu hồn hợp không có kháng thể \(X\)) thì coi như cả 20 mẫu trong nhóm đề không có kháng thể \(X\), còn nếu mẫu hỗn hợp có kháng thể \(X\), thì làm tiếp 20  xét nghiệm, mỗi xét nghiệm cho từng mẫu của nhóm.

a) Xác suất để một mẫu máu hỗn hợp có chứa kháng thể \(X\) là bao nhiêu?

b) Gọi \(S\) là tổng số lần phải xét nghiệm cho cả 6 nhóm. Tính kì vọng và phương sai của biễn ngẫu nhiên rời rạc \(S\) (làm trong kết quả đề hàng phần trăm).

c) Chứng minh rằng số lần xét nghiệm trung bình cho 120 mẫu máu đó theo cách ghép nhóm trên là hơn 48.

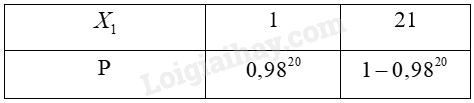
Lời giải chi tiết

a) Gọi \(Y\) là số mẫu máu trong một hỗn hợp máu chứa kháng thể \(X\). Khi đó \(Y\) là biến ngẫu nhiên rời rạc tuân theo phân phối nhị thức với tham số \(n = 20\) ; \(p = 2\%  = 0,02\).

Một hỗn hợp máu có chứa kháng thể \(X\) tức là trong hỗn hợp máu đấy có ít nhất một mẫu máu chứa kháng thể \(X\)

\(\) \({\rm{P(Y}} \ge 1) = 1 - {\rm{P(Y = 0)}} = 1 - C_{20}^0.{(0,02)^0}.{(1 - 0,02)^{20 - 0}} = 1 - {0,98^{20}} \approx 0,3324\)

Vậy xác suất để một mẫu máu hỗn hợp chứa kháng thể \(X\)là 0,3324.

b) Gọi \({X_i}\) là số lần xét nghiệm ở nhóm thứ \(i\) \((i = 1,2,3,4,5,6)\)

Ta có \({\rm{E(}}{{\rm{X}}_{\rm{1}}}{\rm{) = E(}}{{\rm{X}}_{\rm{2}}}{\rm{) = E(}}{{\rm{X}}_{\rm{3}}}{\rm{) = E(}}{{\rm{X}}_{\rm{4}}}{\rm{) = E(}}{{\rm{X}}_{\rm{5}}}{\rm{) = E(}}{{\rm{X}}_{\rm{6}}}{\rm{)}}\)

Vì \({\rm{S = }}{{\rm{X}}_{\rm{1}}}{\rm{ + }}{{\rm{X}}_{\rm{2}}}{\rm{ + }}{{\rm{X}}_{\rm{3}}}{\rm{ + }}{{\rm{X}}_{\rm{4}}}{\rm{ + }}{{\rm{X}}_{\rm{5}}}{\rm{ + }}{{\rm{X}}_{\rm{6}}}\) và các nhóm lại độc lập với nhau nên ta có: \({\rm{E(S) = E(}}{{\rm{X}}_{\rm{1}}}{\rm{) + E(}}{{\rm{X}}_{\rm{2}}}{\rm{) + E(}}{{\rm{X}}_{\rm{3}}}{\rm{) + E(}}{{\rm{X}}_{\rm{4}}}{\rm{) + E(}}{{\rm{X}}_{\rm{5}}}{\rm{) + E(}}{{\rm{X}}_{\rm{6}}}{\rm{) = 6E(}}{{\rm{X}}_{\rm{1}}}{\rm{)}}\)

TH1: Nếu kết quả của mẫu máu hỗn hợp là âm tính thì chỉ cần xét nghiệm 1 lần.

TH2: Nếu kết quả của mẫu máu hỗn hợp là dương tình thì cần xét nghiệm 21 lần tất cả.

Ta có bảng phân bố xác suất:

Do đó ta có \({\rm{E(}}{{\rm{X}}_{\rm{1}}}{\rm{)}} = {1.0,98^{20}} + 21.(1 - {0,98^{20}}) \approx 7,65\)

\({\rm{V(}}{{\rm{X}}_{\rm{1}}}{\rm{)}} = {1^2}{.0,98^{20}} + {21^2}.(1 - {0,98^{20}}) \approx 88,73\)

Vậy \({\rm{E(S)}} = 6.7,65 = 45,9\)  và \({\rm{V(S)}} = 6.88,73 = 532,38.\)

c) Vì \({\rm{E(S)}} = 45,9 < 48\) nên số lần xét nghiệm trung bình cho 120 mẫu ghép nhóm trên là nhỏ hơn 48.