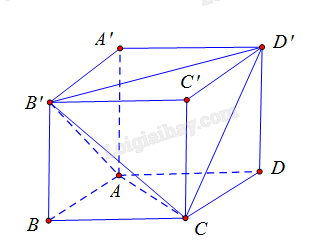
Giải bài 7.49 trang 42 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Cho hình lập phương ABCD.A’B’C’D’ thể tích khối tứ diện ABC’D’ bằng

Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Lí - Hóa - Sinh

Quảng cáo

Đề bài

Cho hình lập phương ABCD.A’B’C’D’ thể tích khối tứ diện ABC’D’ bằng

A. \(\frac{{{a^3}}}{3}\).

B. \(\frac{{{a^3}}}{2}\).

C. \(\frac{{{a^3}}}{6}\).

D. \(\frac{{2{a^3}}}{3}\).

Phương pháp giải - Xem chi tiết

Cách 1: Tính thể tích phần bù

Ta có \({V_{ACB'D'}} = {V_{ABCD.A'B'C'D'}} - \left( {{V_{B'.ABC}} + {V_{C.B'C'D'}} + {V_{D'.ACD}} + {V_{A.A'B'D'}}} \right)\).

Mà \({V_{ABCD.A'B'C'D'}} = {a^3}\) và \({V_{B'.ABC}} = {V_{C.B'C'D'}} = {V_{D'.ACD}} = {V_{A.A'B'D'}} = \frac{1}{3}.A'A.{S_{A'B'D'}} = \frac{1}{3}.a.\frac{1}{2}{a^2} = \frac{1}{6}{a^3}\).

\( \Rightarrow {V_{ACB'D'}} = \)

Cách 2: Sử dụng công thức \({V_{ACB'D'}} = \frac{1}{6}AC.B'D'.d\left( {AC,B'D'} \right).\sin \left( {AC,B'D'} \right)\)

Lời giải chi tiết

Cách 1:

Ta có \({V_{ACB'D'}} = {V_{ABCD.A'B'C'D'}} - \left( {{V_{B'.ABC}} + {V_{C.B'C'D'}} + {V_{D'.ACD}} + {V_{A.A'B'D'}}} \right)\).

Mà \({V_{ABCD.A'B'C'D'}} = {a^3}\) và \({V_{B'.ABC}} = {V_{C.B'C'D'}} = {V_{D'.ACD}} = {V_{A.A'B'D'}} = \frac{1}{3}.A'A.{S_{A'B'D'}} = \frac{1}{3}.a.\frac{1}{2}{a^2} = \frac{1}{6}{a^3}\).

Do đó \({V_{ACB'D'}} = {a^3} - \frac{4}{6}{a^3} = \frac{{{a^3}}}{3}\).

Cách 2: Sử dụng công thức \({V_{ACB'D'}} = \frac{1}{6}AC.B'D'.d\left( {AC,B'D'} \right).\sin \left( {AC,B'D'} \right)\)

\({V_{ACB'D'}} = \frac{1}{6}a\sqrt 2 .a\sqrt 2 .a.\sin {90^ \circ } = \frac{{{a^3}}}{3}\)