SBT Toán 8 - giải SBT Toán 8 - Kết nối tri thức với cuộc sống

Giải bài 7.48 trang 37 sách bài tập toán 8 - Kết nối tri thức với cuộc sống

Một công ty cho thuê thuyền du lịch tính phí thuê thuyền là 1 triệu đồng, ngoài ra tính phí sử dụng là 500 nghìn đồng một giờ.

Tổng hợp đề thi giữa kì 1 lớp 8 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Khoa học tự nhiên

Quảng cáo

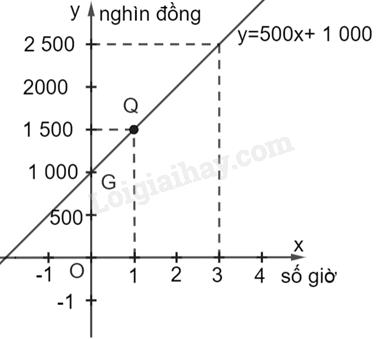
Đề bài

Một công ty cho thuê thuyền du lịch tính phí thuê thuyền là 1 triệu đồng, ngoài ra tính phí sử dụng là 500 nghìn đồng một giờ.

a) Viết công thức của hàm số biểu thị tổng chi phí y (nghìn đồng) để thuê một chiếc thuyền du lịch trong x (giờ)

b) Vẽ đồ thị của hàm số thu được ở câu a để tìm tổng chi phí cho một lần thuê trong 3 giờ.

c) Giao điểm của đồ thị với trục tung biểu thị điều gì?

Phương pháp giải - Xem chi tiết

a) Sử dụng khái niệm hàm số bậc nhất: Hàm số bậc nhất là hàm số cho bởi công thức \(y = ax + b,\) trong đó a, b là các số cho trước và \(a \ne 0\)

b) Sử dụng kiến thức về cách vẽ đồ thị hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\) để vẽ đồ thị:

+ Khi \(b = 0\) thì \(y = ax\). Đồ thị của hàm số \(y = ax\) là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a)

+ Khi \(b \ne 0\), ta thường xác định hai điểm đặc biệt trên đồ thị là giao điểm của đồ thị với hai trục tọa độ như sau:

- Cho \(x = 0\) thì \(y = b\), ta được điểm P(0; b) thuộc trục tung Oy.

- Cho \(y = 0\) thì \(x = \frac{{ - b}}{a}\), ta được điểm \(Q\left( { - \frac{b}{a};0} \right)\) thuộc trục hoành Ox.

- Vẽ đường thẳng đi qua hai điểm P, Q ta được đồ thị của hàm số \(y = ax + b\)

Lời giải chi tiết

a) Phí sử dụng của thuyền du lịch trong x (giờ) là: 500x (nghìn đồng)

Hàm số biểu thị tổng chi phí y (nghìn đồng) để thuê một chiếc thuyền du lịch trong x (giờ) là: \(y = 1\;000 + 500x\) (nghìn đồng)

b) Đồ thị hàm số \(y = 1\;000 + 500x\) (nghìn đồng) đi qua điểm \(G\left( {0;\;1000} \right)\) và điểm \(Q\left( {1;\;1\;500} \right)\)

Nhìn vào đồ thị ta thấy, với \(x = 3\) thì \(y = 2\;500\) (nghìn đồng)

Vậy tổng chi phí cho một lần thuê trong 3 giờ là 2,5 triệu đồng.

c) Giao điểm của đồ thị hàm số với trục tung là (0; 1 000). Giao điểm này biểu thị chi phí thuê tiền cố định khi thuê thuyền (mặc dù không sử dụng giờ nào, tức là \(x = 0\) vẫn phải trả phí này, nếu đã đặt thuê).