Giải bài 6.16 trang 14 sách bài tập toán 10 - Kết nối tri thức với cuộc sốngXác định dấu của các hệ số a, b, c và dấu của biệt thức Quảng cáo
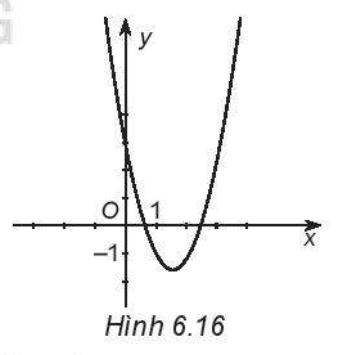
Đề bài Xác định dấu của các hệ số a, b, c và dấu của biệt thức \(\Delta = {b^2} - 4ac\) của hàm số bậc hai \(y = a{x^2} + bx + c\), biết đồ thị của nó có dạng như Hình 6.16.
Phương pháp giải - Xem chi tiết Bước 1: Dựa vào chiều bề lõm quay lên trên/ xuống dưới để tìm dấu của hệ số a Bước 2: Xét dấu của tung độ giao điểm của ĐTHS với trục Oy để tìm dấu của hệ số c Bước 3: Xét dấu tọa độ đỉnh của parabol để xét dấu các biểu thức \( - \frac{b}{{2a}}\) và \( - \frac{\Delta }{{4a}}\). Từ đó suy ra dấu của hệ số b và ∆ Lời giải chi tiết - Do parabol có bề lõm quay lên trên nên a > 0 - ĐTHS cắt trục tung tại điểm có tung độ dương nên c > 0 - Đỉnh parabol có hoành độ dương, tung độ âm nên ta có \(\left\{ \begin{array}{l} - \frac{b}{{2a}} > 0\\ - \frac{\Delta }{{4a}} < 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b < 0\\\Delta > 0\end{array} \right.\) (do a > 0) Vậy a > 0, b < 0, c > 0, ∆ > 0.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
