Giải bài 58 trang 118 sách bài tập toán 11 - Cánh diềuCho tứ diện \(ABCD\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(AB\), \(AD\); \(P\), \(Q\) Quảng cáo
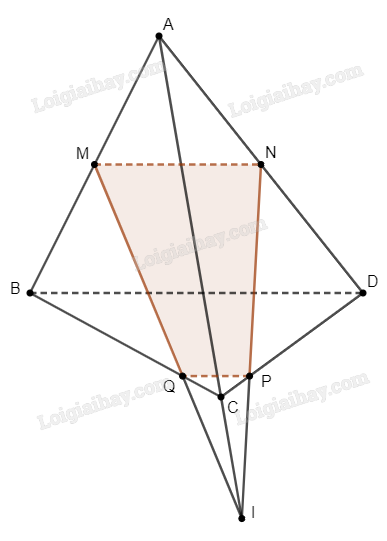
Đề bài Cho tứ diện \(ABCD\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(AB\), \(AD\); \(P\), \(Q\) lần lượt thuộc các cạnh \(CD\), \(BC\) (\(P\), \(Q\) không là trung điểm của \(CD\), \(BC\)). Chứng minh rằng nếu \(M\), \(N\), \(P\), \(Q\) cùng thuộc một mặt phẳng thì ba đường thẳng \(MQ\), \(NP\) và \(AC\) cùng đi qua một điểm. Phương pháp giải - Xem chi tiết Gọi \(I\) là giao điểm của \(NP\) và \(AC\). Ta suy ra rằng \(I\) nằm trên giao tuyến của \(\left( {MNPQ} \right)\) và \(\left( {ABC} \right)\), từ đó suy ra \(I \in MQ\) và điều phải chứng minh. Lời giải chi tiết
Xét \(\left( {ADC} \right)\), do \(P\) không là trung điểm của \(CD\), nên đường thẳng \(NP\) cắt đường thẳng \(AC\). Gọi \(I\) là giao điểm của \(NP\) và \(AC\). Ta có \(I \in \left( {MNPQ} \right)\) (do \(I\) nằm trên \(NP\)) và \(I \in \left( {ABC} \right)\) (do \(I\) nằm trên \(AC\)). Như vậy \(I\) nằm trên giao tuyến của \(\left( {MNPQ} \right)\) và \(\left( {ABC} \right)\). Ta nhận thấy rằng \(\left\{ \begin{array}{l}M \in \left( {MNPQ} \right)\\M \in AB \subset \left( {ABC} \right)\end{array} \right. \Rightarrow M \in \left( {MNPQ} \right) \cap \left( {ABC} \right)\), và \(\left\{ \begin{array}{l}Q \in \left( {MNPQ} \right)\\Q \in BC \subset \left( {ABC} \right)\end{array} \right. \Rightarrow Q \in \left( {MNPQ} \right) \cap \left( {ABC} \right)\). Do đó giao tuyến của \(\left( {MNPQ} \right)\) và \(\left( {ABC} \right)\) là đường thẳng \(MQ\). Mà \(I\) nằm trên giao tuyến của \(\left( {MNPQ} \right)\) và \(\left( {ABC} \right)\), nên \(I \in MQ\). Vậy \(MQ\), \(NP\) và \(AC\) cùng đi qua điểm \(I\). Bài toán được chứng minh.
|




















Danh sách bình luận