Giải bài 56 trang 25 sách bài tập toán 12 - Cánh diềuCho hàm số (y = fleft( x right)) liên tục trên (mathbb{R}) và đồ thị có đường tiệm cận ngang như Hình 10. Hàm số (y = fleft( x right)) có thể là hàm số nào trong các hàm số sau? A. (fleft( x right) = frac{{3{{rm{x}}^2}}}{{{x^2} + x + 1}}). B. (fleft( x right) = frac{{2{{rm{x}}^2}}}{{{x^2} + x + 1}}). C. (fleft( x right) = frac{{{{rm{x}}^2}}}{{{x^2} + x + 1}}). D. (fleft( x right) = frac{{{{rm{x}}^2}}}{{3{x^2} + x + 1}}). Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Quảng cáo
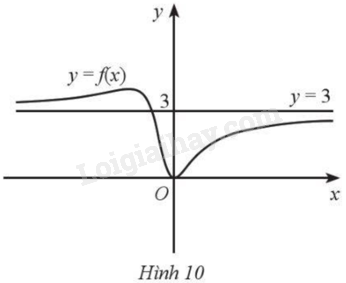
Đề bài Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và đồ thị có đường tiệm cận ngang như Hình 10. Hàm số \(y = f\left( x \right)\) có thể là hàm số nào trong các hàm số sau? A. \(f\left( x \right) = \frac{{3{{\rm{x}}^2}}}{{{x^2} + x + 1}}\). B. \(f\left( x \right) = \frac{{2{{\rm{x}}^2}}}{{{x^2} + x + 1}}\). C. \(f\left( x \right) = \frac{{{{\rm{x}}^2}}}{{{x^2} + x + 1}}\). D. \(f\left( x \right) = \frac{{{{\rm{x}}^2}}}{{3{x^2} + x + 1}}\).
Phương pháp giải - Xem chi tiết ‒ Tìm tiệm cận ngang: Nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\) thì đường thẳng \(y = {y_0}\) là đường tiệm cận ngang. Lời giải chi tiết Dựa vào đồ thị hàm số ta có \(y = 3\) là đường tiệm cận ngang. Xét hàm số: \(f\left( x \right) = \frac{{3{{\rm{x}}^2}}}{{{x^2} + x + 1}}\). Ta có: \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{3{{\rm{x}}^2}}}{{{x^2} + x + 1}} = 3;\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{{3{{\rm{x}}^2}}}{{{x^2} + x + 1}} = 3\). Vậy \(y = 3\) là tiệm cận ngang của đồ thị hàm số \(f\left( x \right) = \frac{{3{{\rm{x}}^2}}}{{{x^2} + x + 1}}\). Chọn A.  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
