Bài 55 trang 134 Vở bài tập toán 8 tập 1

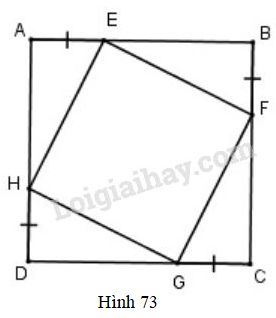
Đề bài

Cho hình \(73\), trong đó \(ABCD\) là hình vuông. Chứng minh rằng tứ giác \(EFGH\) là hình vuông. 

Lời giải chi tiết

Theo tính chất hình vuông, ta có:

 \(AB=BC=CD=DA\)

Theo giả thiết, \(AE = BF = CG = DH\)

Suy ra \(EB=FC=GD=HA\)

\(∆AEH \) và \(  ∆BFE\) có:

\(AE = BF \) (gt)

\(HA=EB\) (chứng minh trên)

\(\widehat A = \widehat B = {90^o}\)

Do đó \(∆AEH =  ∆BFE \) (c.g.c), suy ra \(HE=EF\) (hai cạnh tương ứng).

Chứng minh tương tự ta có \(EF=FG, FG=GH, GH=HE\)

Tứ giác \(EFGH\) có \(HE = EF = FG = GH\) nên là hình thoi    (1)

\(∆AEH =  ∆BFE \) (chứng minh trên) suy ra \(\widehat{AEH} = \widehat{BFE}\) (hai góc tương ứng)

Ta lại có \(\widehat {BEF} + \widehat {BFE} = {90^o}\) nên \(\widehat {AEH} + \widehat {BEF} = {90^o}\) suy ra \(\widehat {HEF} = {90^o}\)        (2)

Từ (1) và (2) suy ra \(EFGH\) là hình vuông (hình thoi có một góc vuông là hình vuông).

Loigiaihay.com