Giải bài 54 trang 118 sách bài tập toán 11 - Cánh diềuCho tứ diện \(ABCD\). Trên cạnh \(BC\) lấy điểm \(M\) sao cho \(MB = 2MC\). Quảng cáo
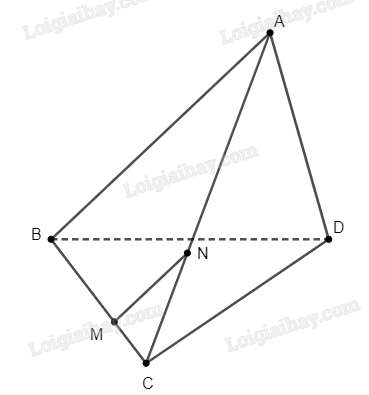
Đề bài Cho tứ diện \(ABCD\). Trên cạnh \(BC\) lấy điểm \(M\) sao cho \(MB = 2MC\). Mặt phẳng \(\left( P \right)\) đi qua \(M\) và song song với mặt phẳng \(\left( {ABD} \right)\) cắt cạnh \(AC\) tại \(N\). Tỉ số \(\frac{{AN}}{{NC}}\) bằng: A. \(\frac{1}{2}\) B. \(1\) C. \(2\) D. \(3\) Phương pháp giải - Xem chi tiết Chứng minh rằng \(MN\parallel AB\) và tính tỉ số \(\frac{{AN}}{{NC}}\) bằng định lí Thales. Lời giải chi tiết
Nhận xét rằng \(MN\) chính là giao tuyến của mặt phẳng \(\left( P \right)\) và \(\left( {ABC} \right)\). Ta nhận thấy rằng \(AB\) là giao tuyến của \(\left( {ABD} \right)\) và \(\left( {ABC} \right)\). Do \(\left( P \right)\) song song với \(\left( {ABD} \right)\), ta suy ra \(MN\parallel AB\). Tam giác \(ABC\) có \(MN\parallel AB\), nên theo định lí Thales, ta có \(\frac{{AN}}{{NC}} = \frac{{BM}}{{MC}} = 2\). Vậy đáp án đúng là C.
|




















Danh sách bình luận