Giải bài 5 trang 28 Chuyên đề học tập Toán 12 - Cánh diều

Đề bài

Bác Dũng đầu tư không quá 1,2 tỉ đồng vào hai loại cổ phiếu: cổ phiếu A dự kiến chi trả cổ tức bằng tiền với tỉ lệ 5%; cổ phiếu B rủi ro cao hơn dự kiến chi trả cổ tức bằng tiền với tỉ lệ 12%. Giá cổ phiếu A là 30 000 đồng/1 cổ phiếu, giá cổ phiếu B là 40 000 đồng/1 cổ phiếu. Để giảm thiểu rủi ro, bác Dũng quyết định mua số lượng cổ phiếu B không quá 10 000 cổ phiếu. Hỏi bác Dũng nên đầu tư mỗi loại bao nhiêu cổ phiếu để lợi nhuận thu được là lớn nhất.

Lời giải chi tiết

Gọi \(x\) là số cổ phiếu A và \(y\) là số cổ phiếu B bác Dũng cần mua \((x \in N;y \in N)\)

Lợi nhuận bác Dũng thu được là \(T = 30000x.5\%  + 40000y.12\% \)  (đồng) hay \(T = 1500x + 4800y\)  (đồng)

Khi đó, số tiền bác Dũng cần chi ra là \(30000x + 40000y\) (đồng)

Vì bác Dũng muốn đầu tư không quá 1,2 tỉ nên ta có \(30000x + 40000y \le 1200000000\) hay \(3x + 4y \le 120000.\)

Vì lượng cổ phiếu B không quá 10000 cổ phiếu nên ta có \(y \le 10000.\)

Để lợi nhuận thu được là lớn nhất ta có bài toán quy hoạch tuyến tính sau:

\(\left\{ \begin{array}{l}\max (T = 1500x + 4800y)\\3x + 4y \le 120000\\y \le 10000\\x \ge 0\\y \ge 0\end{array} \right.\) (I)

Xét hệ bất phương trình bậc nhất hai ẩn (\(x,y\) là các số thực) sau:

\(\left\{ \begin{array}{l}3x + 4y \le 120000\\y \le 10000\\x \ge 0\\y \ge 0\end{array} \right.\) (II)

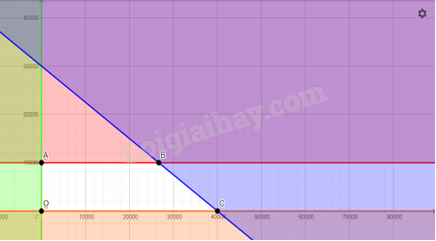
Ta cần tìm giá trị lớn nhất của biểu thức \(T = 1500x + 4800y\) khi \((x,y)\) thoả mãn hệ bất phương trình (II).

Bước 1. Xác định miền nghiệm của hệ bất phương trình (I)

Miền nghiệm là miền tứ giác OABC với toạ độ các đỉnh \(O(0;0);A(0;10000);\)\(B\left( {\frac{{80000}}{3};10000} \right);C(40000;0).\)

Bước 2. Tính giá trị biểu thức \(T(x,y) = 1500x + 4800y\) tại các đỉnh của tứ giác OABC: \(T(0;0) = 0;T(0;10000) = 48000000;\) \(T\left( {\frac{{80000}}{3};10000} \right) = 88000000;T(40000;0) = 60000000.\)

Bước 3. Ta đã biết biểu thức \(T = 1500x + 4800y\) đạt giá trị lớn nhất tại cặp số thực \((x,y)\) là toạ độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được ở bước 2  kết hợp với điều kiện \(x,y\) là các số tự nhiên ta được giá trị lớn nhất cần tìm là \(T(40000;0) = 60000000.\)

Vậy bác Dũng nên đầu tư mua 40 000 cổ phiếu loại A để thu được lợi nhuận lớn nhất.