Giải bài 2 trang 27 Chuyên đề học tập Toán 12 - Cánh diều

Đề bài

Nhu cầu canxi tối thiểu cho một người đang độ tuổi trưởng thành trong một ngày là 1 305 mg. Trong một 1 lạng (100g) đậu nành có 165 mg canxi, 1 lạng thịt có 15 mg canxi. Gia đình chị Thảo có bốn người đang độ tuổi trưởng thành dự định ăn mỗi ngày tối thiểu 3 lạng đậu nàng và 7 lạng thịt, những ăn không quá 4 kg cả đậu nành và thịt. Giá tiền đậu nành là 50 000 đồng/1 kg; giá tiền thịt là 85 000 đồng/1 kg. Hỏi gia đình chị Thảo cần mua bao nhiêu lạng mỗi loại đậu nành và thịt sao cho chi phí để mua hai loại thực phẩm đó là nhỏ nhất?

Lời giải chi tiết

Gọi \(x,y\) (lạng) lần lượt là khối lượng đậu nành và thịt chị Thảo cần mua trong 1 ngày \((x,y \ge 0)\)

Số tiền chị Thảo cần chi trả là \(T = 5000x + 8500y\) (đồng)

Khối lượng canxi có trong \(x\) lạng đậu nành và \(y\) lạng thịt là \(165x + 15y\) (mg)

Vì nhu cầu tối thiểu cho một người đang ở độ tuổi trưởng thành trong 1 ngày là 1 305 mg canxi mà gia đình chị Thảo có 4 người nên ta có: \(165x + 15y \ge 4.1305\)  hay \(165x + 15y \ge 5220\)

Vì gia đình chị Thảo dự định ăn một ngày tối thiểu 3 lạng đậu nành và 7 lạng thịt nhưng không quá 4 kg cả đậu nành và thịt nên ta có \(\left\{ \begin{array}{l}x \ge 3\\y \ge 7\\x + y \le 40\end{array} \right.\)

Vì chị Thảo cần mua đậu nành và thịt sao cho chi phí để mua là thấp nhất nên ta có bài toán quy hoạch tuyến tính sau: l

\(\left\{ \begin{array}{l}\min (T = 5000x + 8500y)\\165x + 15y \ge 5220\\x \ge 3\\y \ge 7\\x + y \le 40\end{array} \right.\)  (I)

Xét hệ bất phương trình bậc nhất hai ẩn (\((x,y)\) là các số thực)

\(\left\{ \begin{array}{l}165x + 15y \ge 5220\\x \ge 3\\y \ge 7\\x + y \le 40\end{array} \right.\) (II)

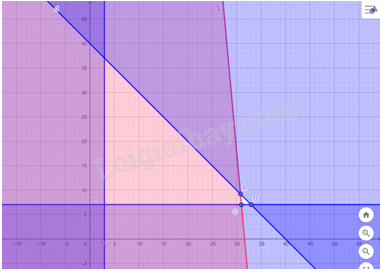
Ta cần tìm giá trị nhỏ nhất của biểu thức \(T = 5000x + 8500y\) khi \((x,y)\) thoả mãn hệ bất phương trình (II)

Bước 1. Xác định miền nghiệm của bất phương trình (II)

Miền nghiệm là miền tam giác \(ABC\) với toạ độ đỉnh \(A(30,8;9,2);\) \(B(33;7);\) \(C(31,7)\).

Bước 2. Tính giá trị biểu thức \(T(x,y) = 5000x + 8500y\) tại các đỉnh của tam giác \(ABC\) ta được \(T(30,8;9,2) = 232200;\) \(T(31;7) = 214500;\) \(T(33;7) = 224500\).

Bước 3. Ta biết biểu thức \(T = 5000x + 8500y\) đạt giá trị nhỏ nhất tại cặp số thực \((x,y)\) là toạ độ một trong các đỉnh của tam giác \(ABC\). So sánh ba giá trị thu được của \(T\) ở bước 2 ta được giá trị nhỏ nhất cần tìm là \(T(31;7) = 214500\).

Vậy gia đình chị Thảo cần mua 31 lạng đậu nành và 7 lạng thịt để chi phí mua hai loại thực phẩm đó là nhỏ nhất.\(\)