Giải bài 5 trang 22 Chuyên đề học tập Toán 12 - Chân trời sáng tạoChi phí để sản xuất (x) sản phẩm là (Cleft( x right) = 2500 + 10x + frac{1}{4}{x^2}) (nghìn đồng). Chi phí trung bình trên mỗi sản phẩm là thấp nhất khi số lượng sản phẩm được sản xuất là A. 20. B. 50. C. 100. D. 1000. Quảng cáo
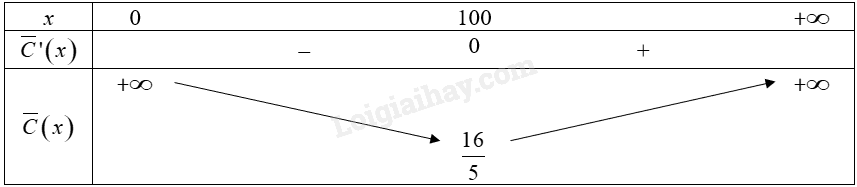
Đề bài Chi phí để sản xuất \(x\) sản phẩm là \(C\left( x \right) = 2500 + 10x + \frac{1}{4}{x^2}\) (nghìn đồng). Chi phí trung bình trên mỗi sản phẩm là thấp nhất khi số lượng sản phẩm được sản xuất là A. 20. B. 50. C. 100. D. 1000. Phương pháp giải - Xem chi tiết • Chi phí trung bình để sản xuất một sản phẩm là \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x}\). • Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm: ‒ Lập bảng biến thiên của hàm số trên tập hợp đó. ‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số. Lời giải chi tiết Chi phí trung bình để sản xuất mỗi sản phẩm là \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{2500 + 10x + \frac{1}{4}{x^2}}}{x} = \frac{{2500}}{x} + 10 + \frac{x}{4}\) với \(x > 0\). b) Ta có: \(\overline C '\left( x \right) = - \frac{{10}}{{{x^2}}} + 0,001\) \(\overline C '\left( x \right) = 0 \Leftrightarrow - \frac{{10}}{{{x^2}}} + 0,001 = 0 \Leftrightarrow {x^2} = 10000 \Leftrightarrow x = 100\) hoặc \(x = - 100\) (loại). Bảng biến thiên của hàm số trên khoảng \(\left( {0; + \infty } \right)\):
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} S = f\left( {100} \right) = \frac{{16}}{5}\). Vậy chi phí trung bình để sản xuất một sản phẩm thấp nhất khi mỗi tuần xưởng sản xuất 100 nghìn sản phẩm. Chọn C  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
