Giải bài 4.62 trang 74 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

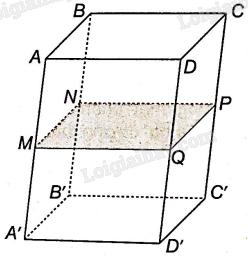
Đề bài

Cho hình hộp ABCD.A’B’C’D’. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AA’, BB’, CC’, DD’. Chứng minh rằng bốn điểm M, N, P, Q đồng phẳng và MNPQ là hình bình hành.

Lời giải chi tiết

Vì M, N lần lượt là trung điểm của hai cạnh AA’, BB’ của hình bình hành ABB’A’ nên MN//AB, mà AB nằm trong mặt phẳng ABCD nên MN//(ABCD)

Tương tự ta có: NP//(ABCD)

Do đó, (MNP)//(ABCD)

Tương tự ta có: (NPQ)//(ABCD)

Qua N có hai mặt phẳng (MNP) và (NPQ) cùng song song với mặt phẳng (ABCD) nên hai mặt phẳng (MNP) và (NPQ) trùng nhau, tức là bốn điểm M, N, P, Q đồng phẳng.

Chứng minh được: MN//PQ và \(MN = PQ\left( { = \frac{1}{2}AB} \right)\) nên tứ giác MNPQ là hình bình hành.