Giải bài 4.33 trang 65 sách bài tập toán 10 - Kết nối tri thức với cuộc sốngCho tam giác ABC không cân. Gọi D,E,F theo thứ tự là chân các đường cao kẻ từ A,B,C; gọi M,N,P tương ứng là trung điểm các cạnh BC,CA,AB. Quảng cáo
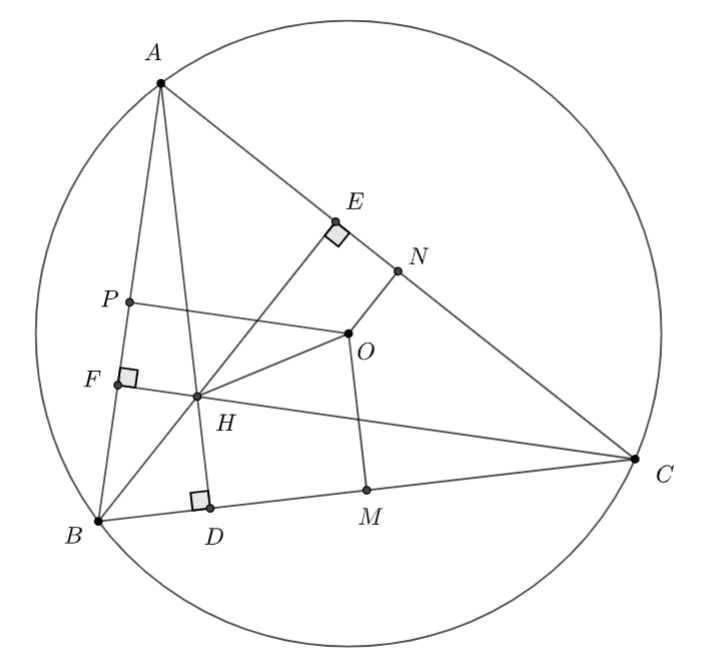
Đề bài Cho tam giác \(ABC\) không cân. Gọi \(D,\,\,E,\,\,F\) theo thứ tự là chân các đường cao kẻ từ \(A,\,\,B,\,\,C;\) gọi \(M,\,\,N,\,\,P\) tương ứng là trung điểm các cạnh \(BC,\,\,CA,\,\,AB.\) Chứng minh rằng \(\overrightarrow {MD} .\overrightarrow {BC} + \overrightarrow {NE} .\overrightarrow {CA} + \overrightarrow {PF} .\overrightarrow {AB} = 0\) Phương pháp giải - Xem chi tiết - Gọi \(H\) là trực tâm và \(O\) là tâm đường tròn ngoại tiếp \(\Delta ABC\) - Áp dụng định lý chiếu để tính tích vô hướng của các vectơ sau \(\overrightarrow {MD} .\overrightarrow {BC} ,\) \(\overrightarrow {NE} .\overrightarrow {CA} \) và \(\overrightarrow {PF} .\overrightarrow {AB} \) Lời giải chi tiết
Gọi \(H\) là trực tâm và \(O\) là tâm đường tròn ngoại tiếp \(\Delta ABC\) Ta có: \(ON \bot AC,\) \(OM \bot BC,\) \(OP \bot AB\) (quan hệ giữa đường kính và dây cung) Áp dụng định lý chiếu ta có: \(\overrightarrow {MD} .\overrightarrow {BC} = \overrightarrow {OH} .\left( {\overrightarrow {OC} - \overrightarrow {OB} } \right) = \overrightarrow {OH} .\overrightarrow {OC} - \overrightarrow {OH} .\overrightarrow {OB} \) (1) \(\overrightarrow {NE} .\overrightarrow {CA} = \overrightarrow {OH} .\left( {\overrightarrow {OA} - \overrightarrow {OC} } \right) = \overrightarrow {OH} .\overrightarrow {OA} - \overrightarrow {OH} .\overrightarrow {OC} \) (2) \(\overrightarrow {PF} .\overrightarrow {AB} = \overrightarrow {OH} .\left( {\overrightarrow {OB} - \overrightarrow {OA} } \right) = \overrightarrow {OH} .\overrightarrow {OB} - \overrightarrow {OH} .\overrightarrow {OA} \) (3) Từ (1), (2) và (3) \( \Rightarrow \) \(\overrightarrow {MD} .\overrightarrow {BC} + \overrightarrow {NE} .\overrightarrow {CA} + \overrightarrow {PF} .\overrightarrow {AB} = 0\) (đpcm)
|




















Danh sách bình luận