Giải bài 4.22 trang 58 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

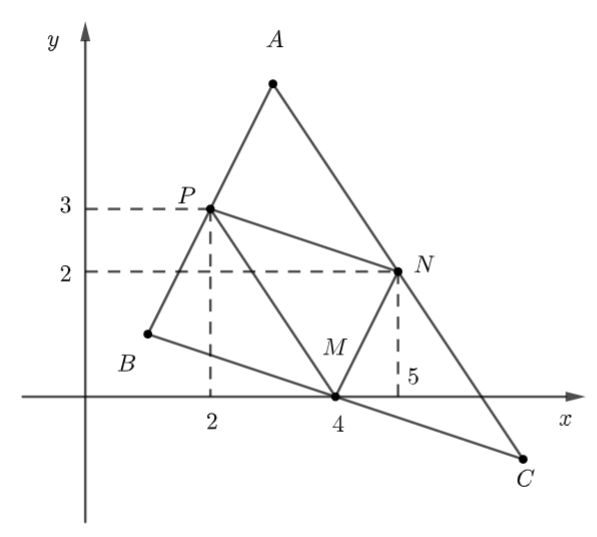
Đề bài

Trong mặt phẳng tọa độ \(Oxy\) cho ba điểm \(M(4;0),\,\,N(5;2)\) và \(P(2;3).\) Tìm tọa độ các đỉnh của tam giác \(ABC,\) biết \(M,\,\,N,\,\,P\) theo thứ tự là trung điểm các cạnh \(BC,\,\,CA,\,\,AB.\)

Lời giải chi tiết

Ta có: \(MN,\,\,NP,\,\,MP\) là đường trung bình của \(\Delta ABC\)

\( \Rightarrow \) \(MN\)//\(AB\), \(NP\)//\(BC\), \(MP\)//\(AC\).

\( \Rightarrow \) \(APMN\), \(BPNM\), \(CMPN\) là hình bình hành

Xét hình bình hành \(APMN\) có:

\(\begin{array}{l}\overrightarrow {OA}  = \overrightarrow {OP}  + \overrightarrow {ON}  - \overrightarrow {OM} \\ \Rightarrow \overrightarrow {OA}  = (2;3) + (5;2) - (4;0) = (3;5)\end{array}\)

\( \Rightarrow \) Tọa độ điểm \(A\) là: \(A(3;5).\)

Xét hình bình hành \(BPNM\) có:

\(\begin{array}{l}\overrightarrow {OB}  = \overrightarrow {OP}  + \overrightarrow {OM}  - \overrightarrow {ON} \\ \Rightarrow \overrightarrow {OB}  = (2;3) + (4;0) - (5;2) = (1;1)\end{array}\)

\( \Rightarrow \) Tọa độ điểm \(B\) là: \(B(1;1).\)

Xét hình bình hành \(CMPN\) có:

\(\begin{array}{l}\overrightarrow {OC}  = \overrightarrow {ON}  + \overrightarrow {OM}  - \overrightarrow {OP} \\ \Rightarrow \overrightarrow {OC}  = (5;2) + (4;0) - (2;3) = (7; - 1)\end{array}\)

\( \Rightarrow \) Tọa độ điểm \(C\) là: \(C(7; - 1).\)