Giải bài 42 trang 104 sách bài tập toán 11 - Cánh diềuCho hình chóp \(S.ABC\) có \(\widehat {ASB} = \widehat {ASC} = {90^o}\). Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh Quảng cáo
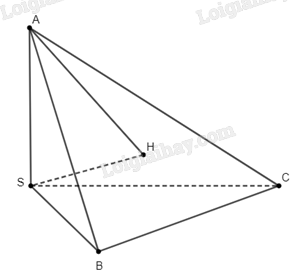
Đề bài Cho hình chóp \(S.ABC\) có \(\widehat {ASB} = \widehat {ASC} = {90^o}\). Gọi \(H\) là trực tâm của tam giác \(ABC\). Chứng minh rằng \(\left( {SAH} \right) \bot \left( {ABC} \right)\). Phương pháp giải - Xem chi tiết Để chứng minh 2 mặt phẳng vuông góc, ta cần chứng minh 1 đường thẳng nằm trong mặt phẳng này vuông góc với mặt phẳng kia. Lời giải chi tiết
Do \(H\) là trực tâm của tam giác \(ABC\) nên ta có \(AH \bot BC\). Do \(\widehat {ASB} = \widehat {ASC} = {90^o}\) nên ta suy ra \(SA \bot SB\) và \(SA \bot SC\). Suy ra \(SA \bot \left( {BSC} \right)\), từ đó \(SA \bot BC\). Như vậy, vì \(AH \bot BC\), \(SA \bot BC\) nên \(\left( {SAH} \right) \bot BC\). Mà \(BC \subset \left( {ABC} \right)\), nên \(\left( {SAH} \right) \bot \left( {ABC} \right)\). Bài toán được chứng minh.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
