Giải bài 4.18 trang 59 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Đề bài

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB//CD). Gọi E, F lần lượt là trọng tâm của các tam giác SAD, SBC.

a) Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. Chứng minh rằng EF//MN, từ đó suy ra EF//AB.

b) Xác định các giao tuyến của mặt phẳng (AEF) với các mặt của hình chóp.

c) Trong các giao tuyến tìm được ở câu b, giao tuyến nào song song với đường thẳng EF?

Lời giải chi tiết

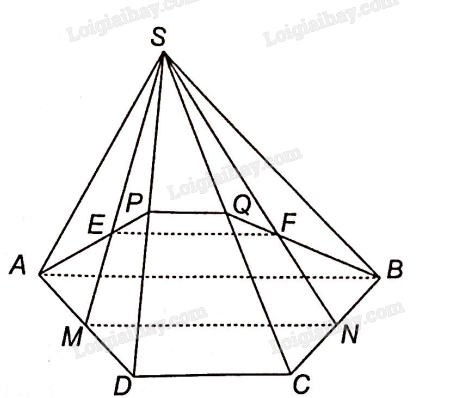
a) E là trọng tâm tam giác SAD nên SE = 2EM.

F là trọng tâm tam giác SBC nên SF = 2FN.

Xét tam giác SMN, ta có tỉ số \(\frac{{{\rm{SE}}}}{{{\rm{SF}}}}{\rm{ = }}\frac{{{\rm{2EM}}}}{{{\rm{2FN}}}}{\rm{ = }}\frac{{{\rm{EM}}}}{{{\rm{FN}}}}\) nên EF//MN (định lý Thales đảo).

M, N lần lượt là trung điểm của các cạnh AD, BC nên MN là đường trung bình hình thang ABCD. Suy ra MN//AB. Suy ra EF//AB.

b) Vì EF//AB nên A, B, E, F đồng phẳng.

Trong mặt phẳng (SAD), gọi P là giao điểm của AE và SD.

Trong mặt phẳng (SCD), gọi Q là giao điểm của BF và SC.

Từ đó P, Q cũng thuộc (ABFE).

Giao tuyến của (AEF) với các mặt của hình chóp lần lượt là: AP, PQ, QB, AB.

c) Có E, F lần lượt là trọng tâm tam giác SAD và SBC nên P là trung điểm của SD, Q là trung điểm của SC.

Suy ra PQ là đường trung bình tam giác SCD. Do đó PQ//CD.

Mà AB//CD suy ra PQ//AB.

Lại có AB//EF suy ra PQ//EF.

Vậy trong các giao tuyến ở câu b), có AB và PQ song song với EF.