Giải Bài 41 trang 81 sách bài tập toán 7 - Cánh diều

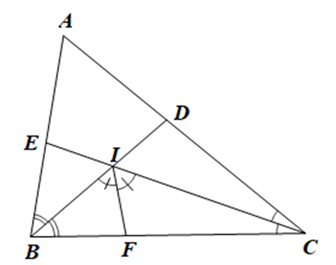
Đề bài

Cho tam giác ABC có ba góc đều nhọn và ˆA=60°.A^=60°.Tia phân giác của góc ABC cắt AC tại D, tia phân giác của góc ACB cắt AB tại E. BD cắt CE tại I. Tia phân giác của góc BIC cắt BC tại F. Chứng minh:

a) \(\widehat {BIC} = 120^\circ \)

b) ∆BEI = ∆BFI;

c) BC = BE + CD.

Lời giải chi tiết

 

a) Vì BD là phân giác của góc ABC nên \(\widehat {ABD} = \widehat {CBD} = \frac{{\widehat {ABC}}}{2}\)

Vì CE là phân giác của góc ACB nên \(\widehat {ACE} = \widehat {ECB} = \frac{{\widehat {ACB}}}{2}\)

Xét ∆ABC có: \(\hat A + \widehat {ABC} + \widehat {ACB} = 180^\circ \) (tổng ba góc của một tam giác)

Suy ra\(\widehat {ABC} + \widehat {ACB} = 180^\circ  - \hat A = 180^\circ  - 60^\circ  = 120^\circ \)

Xét ∆IBC có: \(\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = 180^\circ \) (tổng ba góc của một tam giác)

Hay \(\widehat {BIC} + \frac{{\widehat {ABC}}}{2} + \frac{{\widehat {ACB}}}{2} = 180^\circ \)

Suy ra \(\widehat {BIC} = 180^\circ  - \frac{{\widehat {ABC} + \widehat {ACB}}}{2} = 180^\circ  - \frac{{120^\circ }}{2} = 120^\circ \)

 Vậy \(\widehat {BIC} = 120^\circ .\)

b) Vì IF là phân giác của góc BIC nên \(\widehat {BIF} = \widehat {CIF} = \frac{{\widehat {BIC}}}{2} = \frac{{120^\circ }}{2} = 60^\circ \)

 Ta có \(\widehat {BIC} + \widehat {BIE} = 180^\circ \) (hai góc kề bù)

Suy ra \(\widehat {BIE} = 180^\circ  - \widehat {BIC} = 180^\circ  - 120^\circ  = 60^\circ \)

Xét ∆BEI và ∆BFI có:

\(\widehat {EBI} = \widehat {FBI}\) (chứng minh câu a),

BI là cạnh chung,

\(\widehat {EIB} = \widehat {FIB}\) (cùng bằng 60°),

Do đó ∆BEI = ∆BFI (g.c.g).

Vậy ∆BEI = ∆BFI.

c) Do ∆BEI = ∆BFI (câu b) nên BE = BF (hai cạnh tương ứng).

Ta có \(\widehat {BIC} + \widehat {CID} = 180^\circ \) (hai góc kề bù)

Suy ra \(\widehat {CID} = 180^\circ  - \widehat {BIC} = 180^\circ  - 120^\circ  = 60^\circ \)

Xét ∆CFI và ∆CDI có:

\(\widehat {FCI} = \widehat {DCI}\) (chứng minh câu a),

CI là cạnh chung,

\(\widehat {CIF} = \widehat {CID}\) (cùng bằng 60°),

Suy ra ∆CFI = ∆CDI (g.c.g).

Do đó CF = CD (hai cạnh tương ứng).

Ta có: BC = BF + FC = BE + CD.

Vậy BC = BE + CD.