Giải bài 4 trang 65 sách bài tập toán 8 - Chân trời sáng tạo

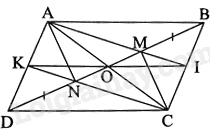
Đề bài

Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho \(BM = DN = \frac{1}{3}BD\).

a) Chứng minh \(\Delta AMB = \Delta CND\).

b) Chứng minh rằng tứ giác AMCN là hình bình hành.

c) Gọi O là giao điểm của AC và BD, I là giao điểm của AM và BC. Chứng minh rằng \(AM = 2MI\).

d) Gọi K là giao điểm của CN và AD. Chứng minh I và K đối xứng với nhau qua O.

Lời giải chi tiết

a) Vì ABCD là hình bình hành nên \(AB = CD\), AB//CD. Do đó, \(\widehat {MBA} = \widehat {NDC}\) (hai góc so le trong)

Tam giác AMB và tam giác CND có:

\(AB = CD\)(cmt), \(\widehat {MBA} = \widehat {NDC}\) (cmt), \(BM = DN\) (gt)

Do đó, \(\Delta AMB = \Delta CND\left( {c - g - c} \right)\)

b) Vì \(\Delta AMB = \Delta CND\) (cmt) nên \(AM = CN\)

Tam giác ABN và tam giác CDM có:

\(AB = CD\)(cmt), \(\widehat {ABN} = \widehat {MDC}\), \(BN = DM\left( { = \frac{2}{3}BD} \right)\)

Suy ra: \(\Delta ABN = \Delta CDM\left( {c - g - c} \right)\) nên \(AN = MC\)

Tứ giác AMCN có: \(AN = MC\) (cmt), \(AM = CN\) (cmt) nên tứ giác AMCN là hình bình hành.

c) Vì tứ giác AMCN là hình bình hành nên \(OA = OC\).

Tam giác ABC có: \(OA = OC\), suy ra BO là đường trung tuyến của tam giác ABC.

Lại có: \(BM = \frac{1}{3}BD,\;BO = \frac{1}{2}BD\), suy ra \(BM = \frac{2}{3}BO\) do đó M là trọng tâm của tam giác ABC. Khi đó, \(AM = \frac{2}{3}AI,MI = \frac{1}{3}AI\). Vậy \(AM = 2MI\)

d) Vì AMCN là hình bình hành nên AM//CN. Mà \(M \in AI,N \in CK\) suy ra AI//CK (1)

mà AD//BC (do ABCD là hình bình hành) và \(K \in AD,I \in BC\) nên AK//CI (2)

Từ (1) và (2) suy ra AKCI là hình bình hành. Mà O là trung điểm của AC, suy ra O là trung điểm của KI hay I đối xứng với K qua O.