Giải bài 4 trang 14 Chuyên đề học tập Toán 12 - Chân trời sáng tạoĐể làm một chiếc bánh bao loại X cần 100 g bột mì và 60 g thịt nạc vai. Để làm một chiếc bánh bao loại Y cần 150 g bột mì và 30 g thịt nạc vai. Có thể làm được nhiều nhất bao nhiêu chiếc bánh bao từ 3 kg bột mì và 1,2 kg thịt nạc vai có sẵn? Biết rằng không thiếu các nguyên liệu khác để làm bánh. Quảng cáo
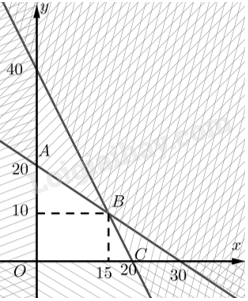
Đề bài Để làm một chiếc bánh bao loại X cần 100 g bột mì và 60 g thịt nạc vai. Để làm một chiếc bánh bao loại Y cần 150 g bột mì và 30 g thịt nạc vai. Có thể làm được nhiều nhất bao nhiêu chiếc bánh bao từ 3 kg bột mì và 1,2 kg thịt nạc vai có sẵn? Biết rằng không thiếu các nguyên liệu khác để làm bánh. Phương pháp giải - Xem chi tiết Bước 1: Đặt hai ẩn biểu thị hai đại lượng chưa biết (cần tìm). Viết điều kiện có nghĩa cho các ẩn đó. Bước 2: Từ dữ kiện của bài toán, viết biểu thức biểu thị đại lượng cần tìm giá trị tối ưu và các bất phương trình bậc nhất đối với hai ẩn trên. Từ đó phát biểu bài toán quy hoạch tuyến tính nhận được. Bước 3: Giải bài toán quy hoạch tuyến tính và trả lời. Lời giải chi tiết Gọi \(x,y\left( {x,y \in \mathbb{N}} \right)\) lần lượt là số bánh bao loại X, loại Y làm được. Có sẵn \(3kg = 3000g\) bột mì nên ta có \(100x + 150y \le 3000\) hay \(2x + 3y - 60 \le 0\). Có sẵn \(1,2kg = 1200g\) thịt nạc vai nên ta có \(60x + 30y \le 1200\) hay \(2x + y - 40 \le 0\). Số bánh bao làm được là \(F = x + y\) (chiếc). Từ đó, ta cần giải bài toán quy hoạch tuyến tính: \(F = x + y \to \max \) với ràng buộc \(\left\{ \begin{array}{l}2x + 3y - 60 \le 0\\2x + y - 40 \le 0\\x \ge 0\\y \ge 0\end{array} \right.\) Tập phương án \({\Omega }\) là miền tứ giác \(OABC\).
Ta có \(A\left( {0;20} \right),C\left( {20;0} \right)\). Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}2{\rm{x}} + 3y = 60\\2{\rm{x}} + y = 40\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 15\\y = 10\end{array} \right.\). Vậy \(B\left( {15;10} \right)\). Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\): \(F\left( {0;20} \right) = 20;F\left( {15;10} \right) = 25;F\left( {6;2} \right) = 8\) Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {15;10} \right) = 25\). Vậy làm được nhiều nhất 15 cái bánh bao loại X và 10 cái bánh bao loại Y.  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
