Giải bài 3.43 trang 90 SGK Toán 8 - Cùng khám pháCho Quảng cáo
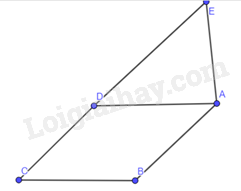
Đề bài Cho \(ABCD\) là hình bình hành có góc \(C\) là góc nhọn. Trên tia đối của tia \(DC\) lấy điểm \(E\) sao cho \(AD = AE\) ( \(E\) khác \(D\)). Chứng minh rằng \(ABCE\) là một hình thang cân. Phương pháp giải - Xem chi tiết Dựa vào tính chất hình bình hành và tính chất hình thang cân để chứng minh. Lời giải chi tiết
Ta có: Tam giác \(ABCD\) là hình bình hành → \(AB//DC\) Mà \(DE\) là cạnh đối của \(DC\) → \(AB//CE\) → Tứ giác \(ABCE\) là hình thang Lại có: \(\widehat {DCB} = \widehat {EDA}\) (do hai góc này ở vị trí đồng vị) Mà \(\widehat {EDA} = \widehat {DEA}\) (do tam giác \(AED\) cân) → \(\widehat {DCB} = \widehat {DEA}\) → Tứ giác \(ABCE\) là hình thang cân vì có hai góc kề 1 đáy bằng nhau.
|




















Danh sách bình luận