Giải bài 3.42 trang 90 SGK Toán 8 - Cùng khám pháTrong Hình 3.95, Quảng cáo
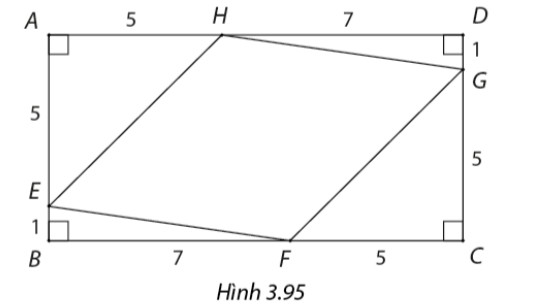
Đề bài Trong Hình 3.95, \(ABCD\) là hình chữ nhật, \(E,F,G,H\) lần lượt là các điểm nằm trên các cạnh \(AB,BC,CD,AD\) và \(BE = DG = 1cm,BF = DH = 7cm,AE = AH = CF = CG = 5cm\). a) Tính độ dài các cạnh của tứ giác \(EFGH\). b) Chứng minh rằng \(HF\) vuông góc với \(EG\).
Phương pháp giải - Xem chi tiết Dựa vào đinh lí Pythagore để tính các cạnh. Lời giải chi tiết a) Độ dài của cạnh \(HE\) là: \(HE = \sqrt {{5^2} + {5^2}} = 5\sqrt 2 \) Độ dài của cạnh \(EF\) là: \(EF = \sqrt {{7^2} + {1^2}} = 5\sqrt 2 \) Độ dài của cạnh \(FG\) là: \(FG = \sqrt {{5^2} + {5^2}} = 5\sqrt 2 \) Độ dài của cạnh \(GH\) là: \(GH = \sqrt {{7^2} + {1^2}} = 5\sqrt 2 \) b) Tứ giác \(EFGH\) có bốn cạnh \(EF = FG = GH = HE = 5\sqrt 2 \) và không có góc vuông. → Tứ giác \(EFGH\) là hình thoi Mà \(HF\) và \(EG\) là hai đường chéo của hình thoi \(EFGH\) → \(HF \bot EG\)
|




















Danh sách bình luận