Giải bài 29 trang 100 sách bài tập toán 8 - Cánh diều

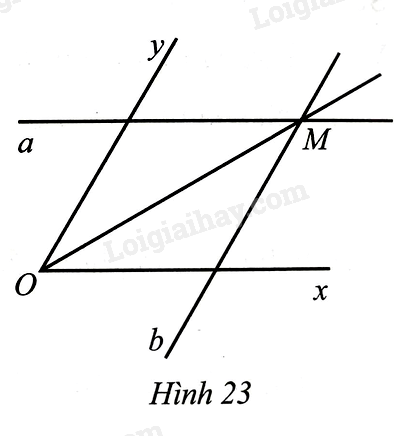
Đề bài

Cho góc \(xOy\) khác góc bẹt. Dùng thước hai lề (thước có hai cạnh song song). Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh \(Ox\) của góc \(xOy\), vẽ đường thẳng \(a\) theo cạnh kia của thước. đặt thước hai lề sao cho một cạnh của thước trùng với cạnh \(Oy\) của góc \(xOy\). Chứng minh tia \(OM\) là tia phân giác của góc \(xOy\).

Lời giải chi tiết

Gọi \(A\) là giao điểm của đường thẳng \(a\) với tia \(Oy\), \(B\) là giao điểm của đường thẳng \(b\) với tia \(Ox\). Kẻ \(AH\) vuông góc với \(OB\) tại \(H,AK\) vuông góc với \(BM\) tại \(K\). Do khoảng cách giữa hai lề của thước là không đổi nên ta có \(AH = AK\).

Tứ giác \(OAMB\) có \(AM//OB,MB//OA\) nên \(OAMB\) là hình bình hành. Suy ra \(\widehat {AOH} = \widehat {AMK}\). Do đó \(\widehat {OAH} = \widehat {MAK}\).

\(\Delta AOH = \Delta AMK\) (cạnh góc vuông – góc nhọn kề). Suy ra \(OA = AM\).

Hình bình hành \(OAMB\) có \(OA = AM\) nên \(OAMB\) là hình thoi. Vậy \(OM\) là tia phân giác của góc \(xOy\).