Bài 24 trang 108 Vở bài tập toán 6 tập 2

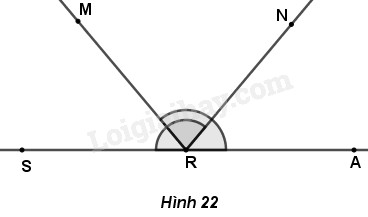
Đề bài

Cho hình 22, trong đó \(S,R,A\) thẳng hàng và \(\widehat {{\rm{AR}}M} = \widehat {SRN} = 130^\circ .\) Tính \(\widehat {{\rm{AR}}N},\,\widehat {{\rm{MRS}}},\,\widehat {{\rm{MR}}N}.\) 

Lời giải chi tiết

Theo đề bài ta có \(S, R, A\) thẳng hàng và điểm \(R\) nằm giữa nên ba điểm đó tạo thành một góc bẹt đỉnh \(R\) hay \(\widehat{SRA}=180^\circ\).

Góc \(SRA\) bẹt nên mọi tia chung gốc \(R\) đều nằm giữa hai tia \(RS,RA\).

• Tia \(RN\) nằm giữa hai tia \(RS,RA\) nên \(\widehat{SRN}+\widehat{NRA}=\widehat{SRA}\)

Hay \(130^\circ+ \widehat{NRA}=180^\circ\)

Suy ra : \(\widehat{NRA}=180^\circ-130^\circ=50^\circ\)

• Chứng minh tương tự, tia \(RM\) nằm giữa hai tia \(RS,RA\) nên \(\widehat{SRM}+\widehat{MRA}=\widehat{SRA}\)

Hay \(130^\circ+ \widehat{MRS}=180^\circ\)

Suy ra : \(\widehat{MRS}=180^\circ-130^\circ=50^\circ\)

• Có \(\widehat{ARM}=130^\circ\); \(\widehat{ARN}=50^\circ\); mà \(50^\circ<130^\circ\) hay \(\widehat{ARN}< \widehat{ARM}\) nên tia \(RN\) nằm giữa hai tia \(RA;RM\).

Suy ra : \(\widehat{ARN}+\widehat{MRN}=\widehat{ARM}\)

Hay \(50^\circ+ \widehat{MRN}=130^\circ\)

Vậy \(\widehat{MRN}=130^\circ-50^\circ=80^\circ\)

Loigiaihay.com