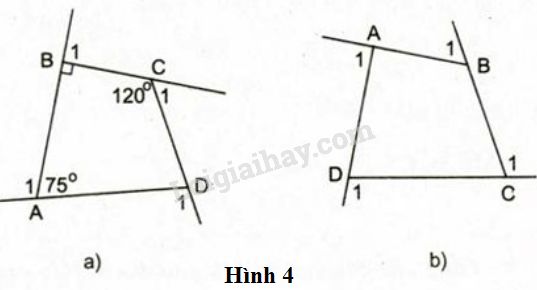
Bài 2 trang 92 Vở bài tập toán 8 tập 1Giải bài 2 trang 92 VBT toán 8 tập 1. Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác. a) Tính các góc ngoài của tứ giác ở hình 4a)... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác. LG a Tính các góc ngoài của tứ giác ở hình 4a) Phương pháp giải: +) Áp dụng định lý: Tổng các góc trong tứ giác bằng \({360^0}\) +) Áp dụng tính chất: Tổng hai góc kề bù bằng \({180^0}\) Lời giải chi tiết: \( \widehat {ADC} = {360^o} - {75^o} - {90^o} - {120^o} \)\(= {75^o} \) \( \widehat {{A_1}} = {180^0} - {75^0} = {105^0} \) \( \widehat {{B_1}} = {180^0} - {90^0} = {90^0} \) \( \widehat {{C_1}} = {180^0} - {120^0} = {60^0} \) Chú ý: \(\widehat {{D_1}} \) và \( \widehat {ADC} \) là \(2\) góc kề bù. \(\widehat {{A_1}} \) và \(\widehat {BAD}\) là \(2\) góc kề bù. \(\widehat {{B_1}} \) và \( \widehat {CBA} \) là \(2\) góc kề bù. \(\widehat {{C_1}} \) và \( \widehat {BCD} \) là \(2\) góc kề bù. LG b Tính tổng các góc ngoài của tứ giác ở hình 4b) (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài): \(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = ?\) Phương pháp giải: +) Áp dụng định lý: Tổng các góc trong tứ giác bằng \({360^0}\) +) Áp dụng tính chất: Tổng hai góc kề bù bằng \({180^0}\) Lời giải chi tiết: \(\begin{array}{l} LG c Có nhận xét gì về tổng các góc ngoài của tứ giác?
Phương pháp giải: +) Áp dụng định lý: Tổng các góc trong tứ giác bằng \({360^0}\) +) Áp dụng tính chất: Tổng hai góc kề bù bằng \({180^0}\) Lời giải chi tiết: Tổng các góc ngoài của một tứ giác bằng \({360^0}\) Loigiaihay.com
|




















Danh sách bình luận