Giải bài 2 trang 45 sách bài tập toán 10 - Chân trời sáng tạo

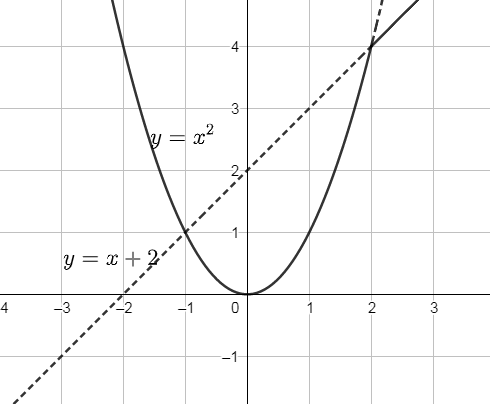
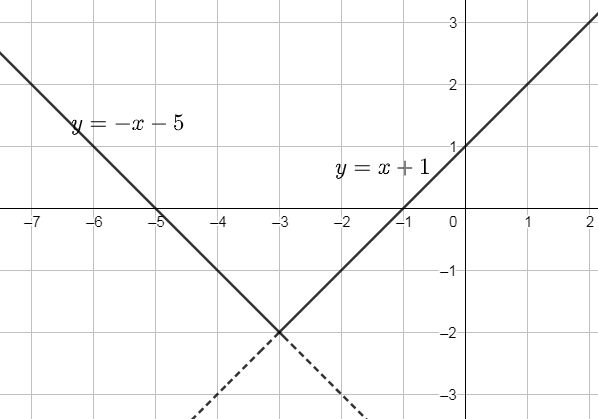
Đề bài

Vẽ đồ thị các hàm số sau:

a) \(f\left( x \right) = \left\{ \begin{array}{l}{x^2}{\rm{       }}\quad x \le 2{\rm{  }}\\x + 2{\rm{   }}\quad x > 2\end{array} \right.\) 

b) \(f\left( x \right) = \left| {x + 3} \right| - 2\)

Lời giải chi tiết

a) Với hàm số \(f\left( x \right) = \left\{ \begin{array}{l}{x^2}{\rm{       }}\quad x \le 2{\rm{  }}\\x + 2{\rm{   }}\quad x > 2\end{array} \right.\)

Ta vẽ đồ thị hàm số \(g\left( x \right) = {x^2}\) và giữ lại phần đồ thị ứng với \(x \le 2\), ta cũng vẽ đồ thị hàm số \(h\left( x \right) = x + 2\)và giữ lại với phần đồ thị \(x > 2\). Ta được đồ thị cần vẽ như sau

 

b) Hàm số đã cho được viết lại như sau:

\(f\left( x \right) = \left| {x + 3} \right| - 2 = \left\{ \begin{array}{l}\left( {x + 3} \right) - 2{\rm{     }}\quad {\rm{ }}x + 3 \ge 0\\ - \left( {x + 3} \right) - 2{\rm{   }}\quad {\rm{ }}x + 3 < 0\end{array} \right. = \left\{ \begin{array}{l}x + 1{\rm{    }}\quad {\rm{ }}x \ge  - 3\\ - x - 5{\rm{  }}\quad {\rm{ }}x <  - 3\end{array} \right.\)

Ta vẽ đồ thị hàm số \(g\left( x \right) = x + 1\) và giữ lại phần đồ thị ứng với \(x \ge  - 3\), ta cũng vẽ đồ thị hàm số \(h\left( x \right) =  - x - 5\)và giữ lại với phần đồ thị \(x <  - 3\). Ta được đồ thị cần vẽ như sau