Giải bài 13 trang 25 Chuyên đề học tập Toán 11 Cánh diều

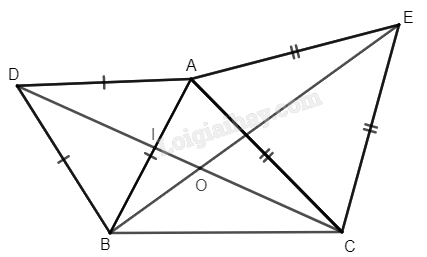
Đề bài

Cho tam giác nhọn ABC. Vẽ về phía ngoài tam giác ABC các tam giác đều ABD, ACE.

a) Xác định ảnh của các điểm D và C quay phép quay tâm A với góc quay \(\varphi  = 60^\circ .\)

b) Chứng minh rằng DC = BE.

c) Chứng minh rằng số đo góc giữa hai đường thẳng DC và BE bằng 60°.

Lời giải chi tiết

a) + Vì tam giác ABD đều nên AD = AB và \(\widehat {DAB} = 60^\circ \).

Phép quay với góc quay φ = 60° có chiều quay ngược chiều kim đồng hồ. Do đó, ảnh của điểm D phép quay tâm A với góc quay \(\varphi  = 60^\circ \) là điểm B.

+ Vì tam giác ACE đều nên AC = AE và \(\widehat {CAE} = 60^\circ \).

Do đó, ảnh của điểm C phép quay tâm A với góc quay \(\varphi  = 60^\circ \) là điểm E.

b) Theo câu a) ta có B và E lần lượt là ảnh của D và C qua phép quay tâm A với góc quay \(\varphi  = 60^\circ \), suy ra DC = BE (phép quay bảo toàn khoảng cách giữa hai điểm bất kì).

c) Gọi O là giao điểm của DC và BE, I là giao điểm của AB và DC.

Ta có phép quay tâm A với góc quay φ = 60° biến góc ADC thành góc ABE nên \(\widehat {ADC} = \widehat {ABE}\) hay \(\widehat {ADI} = \widehat {IBO}\).

Mà \(\widehat {AID} = \widehat {BIO}\) (2 góc đối đỉnh), \(\widehat {ADI} + \widehat {AID} + \widehat {DAI} = 180^\circ \) (tổng ba góc trong tam giác ADI) và \(\widehat {IBO} + \widehat {BIO} + \widehat {IOB} = 180^\circ \) (tổng ba góc trong tam giác IBO).

Từ đó suy ra  \(\widehat {DAI} = \widehat {IOB}\) hay \(\widehat {DOB} = \widehat {DAB} = 60^\circ \).

Như vậy, số đo góc giữa hai đường thẳng DC và BE bằng 60°.