Giải bài 12 trang 95 sách bài tập toán 11 - Chân trời sáng tạo tập 1

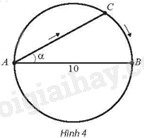
Đề bài

Tại một bể bơi có dạng hình tròn có đường kính \(AB = 10m\), một người xuất phát từ A bơi thẳng theo dây cung AC tạo với đường kính AB một góc \(\alpha \left( {0 < \alpha  < \frac{\pi }{2}} \right)\), rồi chạy bộ theo cung nhỏ CB đến điểm B (Hình 4). Gọi \(S\left( \alpha  \right)\) là quãng đường người đó đã di chuyển.

a) Viết công thức tính \(S\left( \alpha  \right)\) theo \(\alpha \left( {0 < \alpha  < \frac{\pi }{2}} \right)\).

b) Xét tính liên tục của hàm số \(y = S\left( \alpha  \right)\) trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\).

c) Tính các giới hạn \(\mathop {\lim }\limits_{\alpha  \to {0^ + }} S\left( \alpha  \right)\) và \(\mathop {\lim }\limits_{\alpha  \to {{\frac{\pi }{2}}^ + }} S\left( \alpha  \right)\).

Lời giải chi tiết

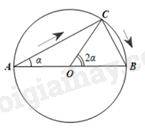
a) Kí hiệu O là tâm hình tròn.

Do tam giác ABC vuông tại C nên \(AC = AB\cos \alpha  = 10\cos \alpha \left( m \right)\)

Ta có: \(\widehat {BOC} = 2\widehat {BAC} = 2\alpha \) nên độ dài cung BC là: \(l = OB.\widehat {BOC} = 5.2\alpha  = 10\alpha \left( m \right)\)

Quãng đường di chuyển của người đó là:

\(S\left( \alpha  \right) = AC + l = 10\cos \alpha  + 10\alpha  = 10\left( {\cos \alpha  + \alpha } \right)\)(m) \(\left( {0 < \alpha  < \frac{\pi }{2}} \right)\)

b) Do các hàm số \(y = \alpha ,y = \cos \alpha \) liên tục trên \(\mathbb{R}\) nên hàm số \(y = S\left( \alpha  \right)\) liên tục trên \(\left( {0;\frac{\pi }{2}} \right)\).

c) \(\mathop {\lim }\limits_{\alpha  \to {0^ + }} S\left( \alpha  \right) = \mathop {\lim }\limits_{\alpha  \to {0^ + }} 10\left( {\alpha  + \cos \alpha } \right) = 10\left( {\mathop {\lim }\limits_{\alpha  \to {0^ + }} \alpha  + \mathop {\lim }\limits_{x \to {0^ + }} \cos \alpha } \right) = 10\left( {0 + 1} \right) = 10\)

\(\mathop {\lim }\limits_{\alpha  \to {{\left( {\frac{\pi }{2}} \right)}^ + }} S\left( \alpha  \right) = \mathop {\lim }\limits_{\alpha  \to {{\left( {\frac{\pi }{2}} \right)}^ + }} 10\left( {\alpha  + \cos \alpha } \right) = 10\left( {\mathop {\lim }\limits_{\alpha  \to {{\left( {\frac{\pi }{2}} \right)}^ + }} \alpha  + \mathop {\lim }\limits_{\alpha  \to {{\left( {\frac{\pi }{2}} \right)}^ + }} \cos \alpha } \right) = 10\left( {\frac{\pi }{2} + 0} \right) = 5\pi \)