Bài 11 trang 100 Vở bài tập toán 8 tập 1Giải bài 11 trang 100 VBT toán 8 tập 1. Hình thang ABCD (AB // CD) có góc ACD= góc BDC. Chứng minh rằng ABCD là hình thang cân. Quảng cáo
Đề bài Hình thang \(ABCD\; (AB // CD)\) có \(\widehat{ACD}=\widehat{BDC}\). Chứng minh rằng \(ABCD\) là hình thang cân. Phương pháp giải - Xem chi tiết - Tam giác cân là tam giác có hai cạnh bên bằng nhau, hai góc đáy bằng nhau. - Dấu hiệu nhận biết hình thang cân: Hình thang có hai đường chéo bằng nhau là hình thang cân. Lời giải chi tiết
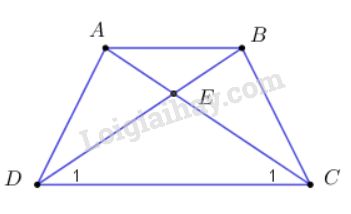
Gọi \(E\) là giao điểm của \(AC\) và \(BD.\) Tam giác \(ECD\) có: \(\widehat {{C_1}} = \widehat {{D_1}}\) nên là tam giác cân, suy ra \( EC = ED\) (1) Chứng minh tương tự \(EA=EB\) (2) Từ (1) và (2) suy ra \(EC+EA=ED+EB\), do đó \(AC=BD\) Hình thang \(ABCD\) có \(AC=BD\) nên là hình thang cân. Giải thích: \(EA=EB\) \({\rm{AB//DC}}\left( \text{giả thiết} \right) \)\(\;\Rightarrow \left\{ \begin{array}{l} Mà: \(\widehat {{C_1}} = \widehat {{D_1}}\left( \text{giả thiết} \right) \Rightarrow \widehat {BA{\rm{E}}} = \widehat {AB{\rm{E}}}\) \( \Rightarrow \Delta ABE\) cân tại \(E\) (dấu hiệu nhận biết tam giác cân) \( \Rightarrow EA=EB\) (tính chất tam giác cân) Loigiaihay.com
|





















Danh sách bình luận