Giải bài 1 trang 88 sách bài tập toán 11 - Cánh diều

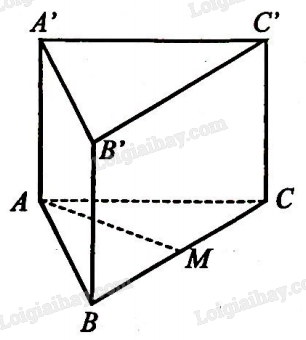
Đề bài

Cho hình lăng trụ \(ABC.A'B'C'\) có \(ABC\) là tam giác đều và \(ABB'A'\) là hình chữ nhật. Gọi M là trung điểm của BC (Hình 4).

 

a) Số đo giữa hai đường thẳng \(AB\) và \(B'C'\) bằng:

A. \({30^0}.\)

B. \({45^0}.\)

C. \({60^0}.\)

D. \({90^0}.\)

b) Số đo giữa hai đường thẳng \(AB\) và \(CC'\) bằng:

A. \({30^0}.\)

B. \({45^0}.\)

C. \({60^0}.\)

D. \({90^0}.\)

c) Số đo giữa hai đường thẳng \(AM\) và \(A'C'\) bằng:

A. \({30^0}.\)

B. \({45^0}.\)

C. \({60^0}.\)

D. \({90^0}.\)

Lời giải chi tiết

a) Do \(ABC\) là tam giác đều nên \(\widehat {ABC} = {60^0}.\)

Ta có: \(BC\)// \(B'C'\) nên \(\left( {AB,B'C'} \right) = \left( {AB,BC} \right) = \widehat {ABC} = {60^0}.\)

Đáp án C.

b) Do \(ABB'A'\) là hình chữ nhật nên \(\widehat {ABB'} = {90^0}.\)

Ta có: \(BB'\)// \(CC'\) nên \(\left( {AB,CC'} \right) = \left( {AB,BB'} \right) = \widehat {ABB'} = {90^0}.\)

Đáp án D.

c) Do \(ABC\) là tam giác đều nên \(\widehat {MAC} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}{.60^0} = {30^0}.\)

Ta có: \(AC\)// \(A'C'\) nên \(\left( {AM,A'C'} \right) = \left( {AM,AC} \right) = \widehat {MAC} = {30^0}.\)

Đáp án A.