Đề thi học kì 1 Toán 12 Cánh diều - Đề số 4Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.Đề bài
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
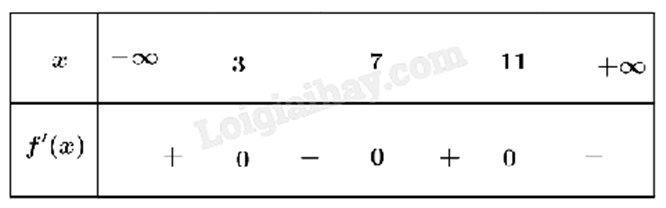
Cho hàm số y = f(x) xác định trên R có bảng xét dấu của f’(x) như hình.
Hàm số f(x) nghịch biến trên khoảng nào dưới đây?
Câu 3 :
Cho hàm số f(x) có đồ thị như hình dưới.
Giá trị nhỏ nhất của hàm số f(x) trên đoạn [0;2] là
Câu 4 :
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{ - 1}}{{2 + x}}\) là
Câu 5 :
Cho hàm số \(f(x) = x - 3 + \frac{1}{{2 - x}}\). Tiệm cận xiên của đồ thị đã cho là đường thẳng
Câu 7 :
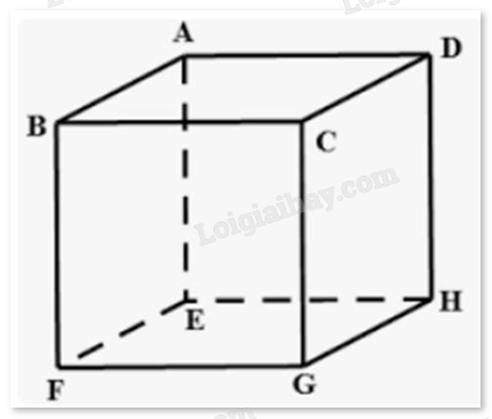
Cho hình hộp ABCD.EFGH. Kết quả phép toán \(\overrightarrow {AB} - \overrightarrow {HF} \) là
Câu 8 :
Cho hình chóp đều S.ABCD tất cả các cạnh bằng \(2\sqrt 3 \) (đvdt). Tính độ dài vecto \(\overrightarrow u = \overrightarrow {SA} - \overrightarrow {SC} \).
Câu 9 :
Trong không gian với hệ tọa độ Oxyz, cho điểm M thỏa mãn \(\overrightarrow {OM} = 2\overrightarrow i + 4\overrightarrow j - 3\overrightarrow k \). Tọa độ điểm M là
Câu 10 :
Trong không gian với hệ trục tọa độ Oxyz, cho hai vecto \(\overrightarrow u = (3;2;1)\) và \(\overrightarrow v = (1;2;3)\). Tính tích vô hướng \(\overrightarrow u .\overrightarrow v \).
Câu 11 :
Trong không gian Oxyz, cho điểm M(4;1;3). Điểm M’ đối xứng với M qua trục Oz có tọa độ
Câu 12 :
Thống kê thời gian dùng mạng xã hội của học sinh lớp 12A như sau:
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Một vật chuyển động thẳng được cho bởi phương trình: \(s(t) = - \frac{1}{3}{t^3} + 4{t^2} + 9t\), trong đó t tính bằng giây và s tính bằng mét. a) Vận tốc của vật tại các thời điểm t = 3 giây là v(3) = 1 m/s.
Đúng
Sai
b) Quãng đường vật đi được từ lúc bắt đầu chuyển động đến khi vật dừng yên là 162(m).
Đúng
Sai
c) Gia tốc của vật tại thời điểm t = 3 giây: a(3) = 2 \(m/{s^2}\).
Đúng
Sai
d) Trong 9 giây đầu tiên, vật tăng tốc khi \(t \in \left[ {0;4} \right]\).
Đúng
Sai
Câu 2 :
Cho tứ diện ABCD. Gọi M, N, P, Q, R, S, G lần lượt là trung điểm các đoạn thẳng AB, CD, AC, BD, AD, BC, MN. a) \(\overrightarrow {MR} = \overrightarrow {SN} \).
Đúng
Sai
b) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
Đúng
Sai
c) \(2\overrightarrow {PQ} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \).
Đúng
Sai
d) \(\left| {\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} } \right|\) nhỏ nhất khi và chỉ khi điểm I trùng với điểm G.
Đúng
Sai
Câu 3 :
Trong không gian Oxyz, cho tam giác ABC với A(1;0;-2), B(-2;3;4), C(4;-6;1). a) Tọa độ trọng tâm G của tam giác là G(1;-1;1).
Đúng
Sai
b) \(\overrightarrow {AB} = (3; - 3;6)\), \(\overrightarrow {AC} = ( - 3;6; - 3)\).
Đúng
Sai
c) Tam giác ABC là tam giác cân.
Đúng
Sai
d) Nếu ABDC là hình bình hành thì tọa độ điểm D là (7;-9;-5).
Đúng
Sai
Câu 4 :
Bảng sau thống kê cân nặng của 50 quả xoài Thanh Ca được lựa chọn ngẫu nhiên sau khi thu hoạch ở một nông trường.
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho (làm tròn kết quả đến chữ số thập phân thứ hai). Đáp án:
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
Một bể chứa ban đầu có 100 lít nước. Sau đó, cứ mỗi phút người ta bơm thêm 20 lít nước, đồng thời cho vào bể 10 gam chất khử trùng (hòa tan). Nồng độ chất khử trùng (gam/lít) sau 10 phút là bao nhiêu (làm tròn đến hàng phần trăm)? Đáp án:
Câu 2 :
Một ngọn hải đăng đạt ở vị trí A cách bờ biển một khoảng AB = 5 (km). Trên bờ biển có một kho hàng ở vị trí C cách B một khoảng là 7 (km). Người canh hải đăng có thể chèo đò từ A đến điểm M trên bờ biển với vận tốc 4 (km/h) rồi đi bộ đến C với vận tốc 6 (km/h). Xác định vị trí của điểm M để người đó đến kho nhanh nhất (làm tròn kết quả đến hàng phần nghìn).
Đáp án:
Câu 3 :
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) \((a,b,c,d \in \mathbb{R})\) có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c, d?
Đáp án:
Câu 4 :
Cho hình lập phương B’C có đường chéo \(A'C = \frac{3}{{16}}\). Gọi O là tâm hình vuông ABCD và điểm S thỏa mãn \(\overrightarrow {OS} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} + \overrightarrow {OD'} \). Khi đó, độ dài đoạn OS bằng \(\frac{{a\sqrt 3 }}{b}\) với \(a,b \in \mathbb{N}\) và \(\frac{a}{b}\) là phân số tối gián. Tính giá trị của biểu thức \(P = {a^2} + {b^2}\). Đáp án:
Câu 5 :
Những căn nhà gỗ trong Hình 1 được phác thảo dưới dạng một hình lăng trụ đứng tam giác OAB⋅O′A′B′. Với hệ trục toạ độ Oxyz thể hiện như Hình 2 (đơn vị đo lấy theo centimét), hai điểm A′ và B′ có tọa độ lần lượt là (240;450;0) và̀ (120;450;300). Mỗi căn nhà gỗ có chiều dài là a cm, chiều rộng là b cm, mỗi cạnh bên của mặt tiền có độ dài là c cm. Tính a + b + c (làm tròn đến hàng đơn vị).
Đáp án:
Câu 6 :
Người ta ghi lại tuổi thọ của một số con ong cho kết quả như sau:
Tính khoảng tứ phân vị của mẫu số liệu (làm tròn kết quả đến hàng phần mười). Đáp án: Lời giải và đáp án
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Cho hàm số y = f(x) xác định trên R có bảng xét dấu của f’(x) như hình.
Hàm số f(x) nghịch biến trên khoảng nào dưới đây?
Đáp án : A Phương pháp giải :
Quan sát bảng xét dấu và nhận xét. Lời giải chi tiết :
Trên khoảng (4;7), f’(x) mang dấu âm nên f(x) nghịch biến trên (4;7).
Đáp án : C Phương pháp giải :
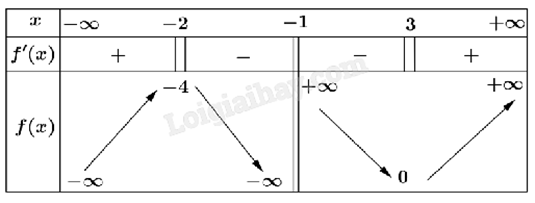
Quan sát bảng biến thiên và nhận xét. Lời giải chi tiết :
Hàm số đạt cực đại tại x = -2.
Câu 3 :
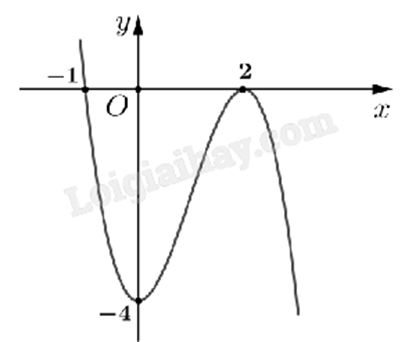
Cho hàm số f(x) có đồ thị như hình dưới.
Giá trị nhỏ nhất của hàm số f(x) trên đoạn [0;2] là
Đáp án : B Phương pháp giải :
Quan sát đồ thị và nhận xét. Lời giải chi tiết :
Giá trị nhỏ nhất của f(x) trên đoạn [0;2] là y = -4 tại x = 0.
Câu 4 :
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{ - 1}}{{2 + x}}\) là
Đáp án : D Phương pháp giải :
Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } f(x) = {y_0}\). Lời giải chi tiết :
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \frac{{ - 1}}{{2 + x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - \frac{1}{x}}}{{\frac{2}{x} + 1}} = \frac{0}{1} = 0\) nên đồ thị hàm số f(x) có tiệm cận ngang là \(y = 0\).
Câu 5 :
Cho hàm số \(f(x) = x - 3 + \frac{1}{{2 - x}}\). Tiệm cận xiên của đồ thị đã cho là đường thẳng
Đáp án : D Phương pháp giải :
Đường thẳng y = ax + b là tiệm cận xiên của đồ thị hàm số f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f(x) - (ax + b)} \right] = 0\). Lời giải chi tiết :
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (x + 1)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ {x - 3 + \frac{1}{{2 - x}} - (x - 3)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{2 - x}} = 0\). Vây y = x + 1 là tiệm cận xiên của đồ thị hàm số.
Đáp án : C Phương pháp giải :
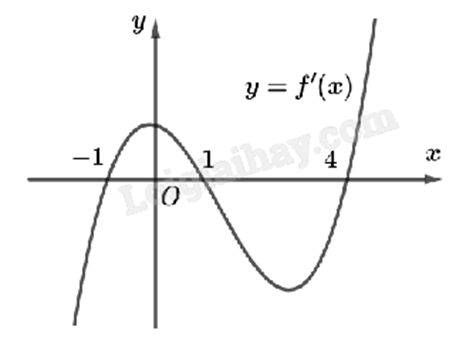
Hàm số f(x) đồng biến khi f’(x) > 0 (phần đồ thị f’(x) nằm phía trên trục hoành). Lời giải chi tiết :
Quan sát đồ thị y = f’(x) ta thấy f’(x) > 0 trên (-1;0) nên f(x) đồng biến trên (-1;0). Chú ý
Đồ thị trong hình là của hàm số f'(x), không phải đồ thị f(x).
Câu 7 :
Cho hình hộp ABCD.EFGH. Kết quả phép toán \(\overrightarrow {AB} - \overrightarrow {HF} \) là
Đáp án : D Phương pháp giải :
Dựa vào khái niệm vecto bằng nhau, vecto đối nhau, quy tắc ba điểm. Lời giải chi tiết :
Ta có \(\overrightarrow {AB} - \overrightarrow {HF} = \overrightarrow {AB} + \overrightarrow {FH} = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \).
Câu 8 :
Cho hình chóp đều S.ABCD tất cả các cạnh bằng \(2\sqrt 3 \) (đvdt). Tính độ dài vecto \(\overrightarrow u = \overrightarrow {SA} - \overrightarrow {SC} \).
Đáp án : C Phương pháp giải :
Sử dụng quy tắc trừ vecto và xác định độ dài vecto. Lời giải chi tiết :
Ta có \(\left| {\overrightarrow u } \right| = \left| {\overrightarrow {SA} - \overrightarrow {SC} } \right| = \left| {\overrightarrow {CA} } \right| = 2\sqrt 6 \).
Câu 9 :
Trong không gian với hệ tọa độ Oxyz, cho điểm M thỏa mãn \(\overrightarrow {OM} = 2\overrightarrow i + 4\overrightarrow j - 3\overrightarrow k \). Tọa độ điểm M là
Đáp án : A Phương pháp giải :
Tọa độ điểm M là tọa độ \(\overrightarrow {OM} \). Lời giải chi tiết :
\(\overrightarrow {OM} = (2;4; - 3)\) suy ra M(2;4;-3).
Câu 10 :
Trong không gian với hệ trục tọa độ Oxyz, cho hai vecto \(\overrightarrow u = (3;2;1)\) và \(\overrightarrow v = (1;2;3)\). Tính tích vô hướng \(\overrightarrow u .\overrightarrow v \).
Đáp án : C Phương pháp giải :
Sử dụng công thức tính tích vô hướng \(\overrightarrow a .\overrightarrow b = {x_a}.{x_b} + {y_a}.{y_b} + {z_a}.{z_b}\). Lời giải chi tiết :
Ta có: \(\overrightarrow u .\overrightarrow v = 1.3 + 2.2 + 3.1 = 10\).
Câu 11 :
Trong không gian Oxyz, cho điểm M(4;1;3). Điểm M’ đối xứng với M qua trục Oz có tọa độ
Đáp án : A Phương pháp giải :
Điểm M’ đối xứng với M(a;b;c) qua trục Oz có tọa độ M’(-a;-b;c). Lời giải chi tiết :
Điểm M’ đối xứng với M(4;1;3) qua trục Oz có tọa độ M’(-4;-1;3).
Câu 12 :
Thống kê thời gian dùng mạng xã hội của học sinh lớp 12A như sau:
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Đáp án : D Phương pháp giải :
Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên chứa dữ liệu. Lời giải chi tiết :
R = 40 – 0 = 40.
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Một vật chuyển động thẳng được cho bởi phương trình: \(s(t) = - \frac{1}{3}{t^3} + 4{t^2} + 9t\), trong đó t tính bằng giây và s tính bằng mét. a) Vận tốc của vật tại các thời điểm t = 3 giây là v(3) = 1 m/s.
Đúng
Sai
b) Quãng đường vật đi được từ lúc bắt đầu chuyển động đến khi vật dừng yên là 162(m).
Đúng
Sai
c) Gia tốc của vật tại thời điểm t = 3 giây: a(3) = 2 \(m/{s^2}\).
Đúng
Sai
d) Trong 9 giây đầu tiên, vật tăng tốc khi \(t \in \left[ {0;4} \right]\).
Đúng
Sai
Đáp án
a) Vận tốc của vật tại các thời điểm t = 3 giây là v(3) = 1 m/s.
Đúng
Sai
b) Quãng đường vật đi được từ lúc bắt đầu chuyển động đến khi vật dừng yên là 162(m).
Đúng
Sai
c) Gia tốc của vật tại thời điểm t = 3 giây: a(3) = 2 \(m/{s^2}\).
Đúng
Sai
d) Trong 9 giây đầu tiên, vật tăng tốc khi \(t \in \left[ {0;4} \right]\).
Đúng
Sai
Phương pháp giải :
Lập bảng biến thiên và nhận xét. Lời giải chi tiết :
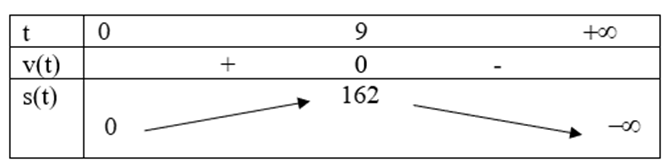
a) Sai. \(v(t) = s'(t) = - {t^2} + 8t + 9\). \(v(3) = - {3^2} + 8.3 + 9 = 24\) (m/s). b) Đúng. \(v(t) = 0 \Leftrightarrow - {t^2} + 8t + 9 = 0 \Leftrightarrow \) x = -1 (loại) hoặc x = 9 (thỏa mãn). Bảng biến thiên:
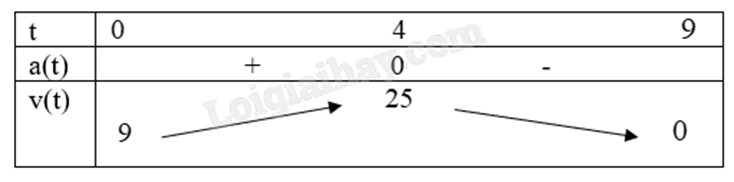
Vậy quãng đường vật di chuyển được từ lúc bắt đầu chuyển động đến khi vật đứng yên (v = 0 hay t = 9) là s(9) – s(0) = 162 – 0 = 162 (m). c) Đúng. \(a(t) = v'(t) = - 2t + 8\). \(a(3) = - 2.3 + 8 = 2\) \(m/{s^2}\). d) Sai. Bảng biến thiên:
Ta thấy tại thời điểm t = 4 thì a(4) = 0, khi đó vật giữ nguyên vận tốc. Vậy vật không tăng tốc khi t = 4, hay \(t \in [0;4]\) là sai.
Câu 2 :
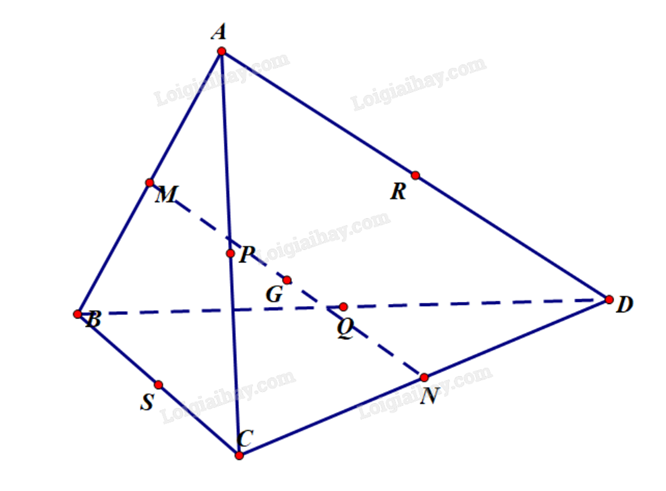
Cho tứ diện ABCD. Gọi M, N, P, Q, R, S, G lần lượt là trung điểm các đoạn thẳng AB, CD, AC, BD, AD, BC, MN. a) \(\overrightarrow {MR} = \overrightarrow {SN} \).
Đúng
Sai
b) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
Đúng
Sai
c) \(2\overrightarrow {PQ} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \).
Đúng
Sai
d) \(\left| {\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} } \right|\) nhỏ nhất khi và chỉ khi điểm I trùng với điểm G.
Đúng
Sai
Đáp án
a) \(\overrightarrow {MR} = \overrightarrow {SN} \).
Đúng
Sai
b) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
Đúng
Sai
c) \(2\overrightarrow {PQ} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \).
Đúng
Sai
d) \(\left| {\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} } \right|\) nhỏ nhất khi và chỉ khi điểm I trùng với điểm G.
Đúng
Sai
Phương pháp giải :
Dựa vào khái niệm vecto cùng phương, cùng hướng, cách xác định độ dài vecto, tính chất trung điểm. Lời giải chi tiết :
a) Đúng. Vì \(\overrightarrow {MR} = \frac{1}{2}\overrightarrow {BD} \), \(\overrightarrow {SN} = \frac{1}{2}\overrightarrow {BD} \) suy ra \(\overrightarrow {MR} = \overrightarrow {SN} \). b) Đúng. Ta có: M là trung điểm của AB nên \(\overrightarrow {GA} + \overrightarrow {GB} = 2\overrightarrow {GM} \). N là trung điểm của CD nên \(\overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {GN} \). G là trung điểm của MN nên \(\overrightarrow {GM} + \overrightarrow {GN} = \overrightarrow 0 \). Từ đó suy ra \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {GM} + 2\overrightarrow {GN} = 2\left( {\overrightarrow {GM} + \overrightarrow {GN} } \right) = \overrightarrow 0 \). c) Sai. Ta có: Q là trung điểm của BD nên \(\overrightarrow {AB} + \overrightarrow {AD} = 2\overrightarrow {AQ} \Leftrightarrow \overrightarrow {AQ} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)\). P là trung điểm của AC nên \(\overrightarrow {AP} = \frac{1}{2}\overrightarrow {AC} \). Từ đó ta có \(2\overrightarrow {PQ} = 2\left( {\overrightarrow {AQ} - \overrightarrow {AP} } \right) = 2\left[ {\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) - \frac{1}{2}\overrightarrow {AC} } \right] = \overrightarrow {AB} - \overrightarrow {AC} + \overrightarrow {AD} \). d) Đúng. Ta có: \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = 2\overrightarrow {IM} + 2\overrightarrow {IN} = 2\left( {\overrightarrow {IM} + \overrightarrow {IN} } \right) = 2.2\overrightarrow {IG} = 4\overrightarrow {IG} \). Suy ra \(\left| {\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} } \right| = \left| {4\overrightarrow {IG} } \right| = 4IG\). Vậy \(\left| {\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} } \right|\) nhỏ nhất khi IG = 0, tức I trùng G.
Câu 3 :
Trong không gian Oxyz, cho tam giác ABC với A(1;0;-2), B(-2;3;4), C(4;-6;1). a) Tọa độ trọng tâm G của tam giác là G(1;-1;1).
Đúng
Sai
b) \(\overrightarrow {AB} = (3; - 3;6)\), \(\overrightarrow {AC} = ( - 3;6; - 3)\).
Đúng
Sai
c) Tam giác ABC là tam giác cân.
Đúng
Sai
d) Nếu ABDC là hình bình hành thì tọa độ điểm D là (7;-9;-5).
Đúng
Sai
Đáp án
a) Tọa độ trọng tâm G của tam giác là G(1;-1;1).
Đúng
Sai
b) \(\overrightarrow {AB} = (3; - 3;6)\), \(\overrightarrow {AC} = ( - 3;6; - 3)\).
Đúng
Sai
c) Tam giác ABC là tam giác cân.
Đúng
Sai
d) Nếu ABDC là hình bình hành thì tọa độ điểm D là (7;-9;-5).
Đúng
Sai
Phương pháp giải :
Sử dụng các quy tắc cộng, trừ vecto, nhân vecto với một số, tọa độ trọng tâm. Lời giải chi tiết :
a) Đúng. Ta có: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{1 - 2 + 4}}{3} = 1\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{0 + 3 - 6}}{3} = - 1\\{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{ - 2 + 4 + 1}}{3} = 1\end{array} \right.\), vậy G\(\left( {1; - 1;1} \right)\). b) Sai. \(\overrightarrow {AB} = ( - 2 - 1;3 - 0;4 + 2) = ( - 3;3;6)\), \(\overrightarrow {AC} = (4 - 1; - 6 - 0;1 + 2) = (3; - 6;3)\). c) Đúng. \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{( - 3)}^2} + {3^2} + {6^2}} = 3\sqrt 6 \), \(AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{3^2} + {{( - 6)}^2} + {3^2}} = 3\sqrt 6 \) suy ra AB = AC. Vậy tam giác ABC cân tại A. d) Sai. Vì ABDC là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {CD} \Leftrightarrow ( - 3;3;6) = ({x_D} - 4;{y_D} + 6;{z_D} - 1)\). Suy ra \(({x_D};{y_D};{z_D}) = (1; - 3;7)\). Vậy D(1;-3;7).
Câu 4 :
Bảng sau thống kê cân nặng của 50 quả xoài Thanh Ca được lựa chọn ngẫu nhiên sau khi thu hoạch ở một nông trường.
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho (làm tròn kết quả đến chữ số thập phân thứ hai). Đáp án: Đáp án
Đáp án: Phương pháp giải :
Công thức: \({\Delta _Q} = {Q_3} - {Q_1}\). Lời giải chi tiết :
Cỡ mẫu: n = 3 + 13 + 18 + 11 + 5 = 50. Gọi \({x_1},{x_2},...,{x_{50}}\) là mẫu số liệu gốc được sắp xếp theo thứ tự không giảm. Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_{13}} \in [290;330)\). \({Q_1} = 290 + \frac{{\frac{{50}}{4} - 3}}{{13}}(330 - 290) = \frac{{4150}}{{13}}\). Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{38}} \in [370;410)\). \({Q_3} = 370 + \frac{{\frac{{3.50}}{4} - (3 + 13 + 18)}}{{11}}(410 - 370) = \frac{{4210}}{{11}}\). Vậy \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{4210}}{{11}} - \frac{{4150}}{{13}} = \frac{{9080}}{{143}} \approx 63,5\).
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
Một bể chứa ban đầu có 100 lít nước. Sau đó, cứ mỗi phút người ta bơm thêm 20 lít nước, đồng thời cho vào bể 10 gam chất khử trùng (hòa tan). Nồng độ chất khử trùng (gam/lít) sau 10 phút là bao nhiêu (làm tròn đến hàng phần trăm)? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Lập hàm số f(t) tính nồng độ chất khử (khối lượng chất khử trên thể tích nước) theo thời gian t phút rồi tính f(10). Lời giải chi tiết :
Số lít nước trong bể chứa sau t phút là 100 + 20t (lít). Số gam chất tan được cho vào bể sau t phút là 10t (gam). Nồng độ chất khử trùng trong bể sau t phút là \(f(t) = \frac{{10t}}{{100 + 20t}} = \frac{t}{{10 + 2t}}\) (gam/lít). Nồng độ chất khử trùng trong bể sau 10 phút là \(f(10) = \frac{{10}}{{10 + 2.10}} = \frac{1}{3} \approx 0,33\) (gam/lít).
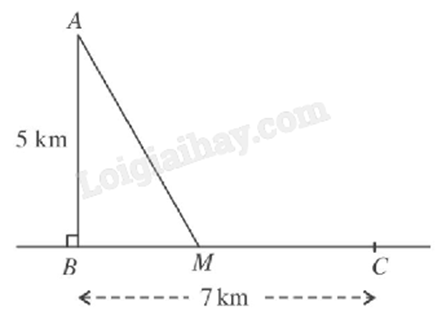
Câu 2 :
Một ngọn hải đăng đạt ở vị trí A cách bờ biển một khoảng AB = 5 (km). Trên bờ biển có một kho hàng ở vị trí C cách B một khoảng là 7 (km). Người canh hải đăng có thể chèo đò từ A đến điểm M trên bờ biển với vận tốc 4 (km/h) rồi đi bộ đến C với vận tốc 6 (km/h). Xác định vị trí của điểm M để người đó đến kho nhanh nhất (làm tròn kết quả đến hàng phần nghìn).
Đáp án: Đáp án
Đáp án: Phương pháp giải :
Thiết lập hàm số biểu diễn thời gian đi từ A đến M và từ M đến C. Tìm giá trị nhỏ nhất của hàm số đó. Lời giải chi tiết :
Đặt x = BM, \(0 \le x \le 7\). Khi đó \(AM = \sqrt {{x^2} + 25} \), \(MC = 7 - x\). Thời gian người canh hải đăng đi từ A đến C là \(T(x) = \frac{{\sqrt {{x^2} + 25} }}{4} + \frac{{7 - x}}{6}\) (giờ). Ta có \(T'(x) = \frac{1}{4}.\frac{{2x}}{{2\sqrt {{x^2} + 25} }} + \frac{1}{6}.( - 1) = \frac{x}{{4\sqrt {{x^2} + 25} }} - \frac{1}{6} = 0 \Leftrightarrow \frac{x}{{4\sqrt {{x^2} + 25} }} = \frac{1}{6}\) \( \Leftrightarrow 6x = 4\sqrt {{x^2} + 25} \Leftrightarrow {x^2} = 20\). Giải phương trình trên kết hợp với điều kiện ta được \(x = 2\sqrt 5 \). Có \(T(0) = \frac{{\sqrt {{0^2} + 25} }}{4} + \frac{{7 - 0}}{6} = \frac{5}{4} + \frac{7}{6} = \frac{{29}}{{12}} \approx 2,417\); \(T(2\sqrt 5 ) = \frac{{\sqrt {{{\left( {2\sqrt 5 } \right)}^2} + 25} }}{4} + \frac{{7 - 2\sqrt 5 }}{6} = \frac{5}{4} + \frac{7}{6} = \frac{{4 + 5\sqrt 5 }}{{12}} \approx 2,098\); \(T(7) = \frac{{\sqrt {{7^2} + 25} }}{4} + \frac{{7 - 7}}{6} = \frac{{\sqrt {74} }}{4} \approx 2,151\). Từ đó suy ra T(x) đạt giá trị nhỏ nhất khi \(x = 2\sqrt 5 \approx 4,472\). Vậy để người canh hải đăng đi từ hải đăng đến kho hàng nhanh nhất thì điểm M cách B một khoảng 4,472 km.
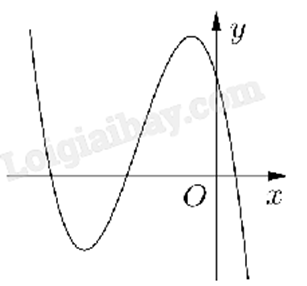
Câu 3 :
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) \((a,b,c,d \in \mathbb{R})\) có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c, d?
Đáp án: Đáp án
Đáp án: Phương pháp giải :
Tìm đạo hàm rồi xác định dấu của a, b, c, d dựa vào các đặc điểm của đồ thị. Lời giải chi tiết :
Có \(y' = 3a{x^2} + 2bx + c\). Quan sát đồ thị thấy \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \) suy ra a < 0. Hàm số có hai cực trị âm nên ta có \(\left\{ \begin{array}{l}{\Delta _{y'}} > 0\\S < 0\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{b^2} - 9ac > 0\\ - \frac{{2b}}{{3a}} < 0\\\frac{c}{{3a}} > 0\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}b < 0\\c < 0\end{array} \right.\) Đồ thị cắt trục Oy tại điểm (0;d) nên d > 0. Vậy chỉ có d dương.
Câu 4 :
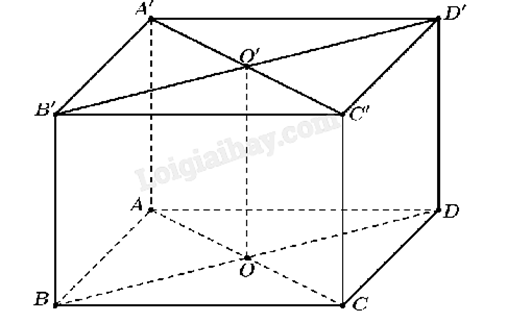
Cho hình lập phương B’C có đường chéo \(A'C = \frac{3}{{16}}\). Gọi O là tâm hình vuông ABCD và điểm S thỏa mãn \(\overrightarrow {OS} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} + \overrightarrow {OD'} \). Khi đó, độ dài đoạn OS bằng \(\frac{{a\sqrt 3 }}{b}\) với \(a,b \in \mathbb{N}\) và \(\frac{a}{b}\) là phân số tối gián. Tính giá trị của biểu thức \(P = {a^2} + {b^2}\). Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng tính chất trung điểm, quy tắc nhân vecto với một số và cách xác định độ dài vecto. Lời giải chi tiết :
Gọi O’ là tâm hình vuông A’B’C’D’. Xét tam giác AA’C’ vuông tại A: \(A'{C^2} = A'{A^2} + A{C^2} = A'{A^2} + {\left( {\sqrt 2 A'A} \right)^2} = 3A'{A^2}\). Suy ra \(A'A = \frac{{A'C}}{{\sqrt 3 }} = \frac{{\sqrt 3 }}{{16}}\). Ta có: \(\overrightarrow {OS} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} + \overrightarrow {OD'} \) \( = \left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {OB} + \overrightarrow {OD} } \right) + \left( {\overrightarrow {OA'} + \overrightarrow {OC'} } \right) + \left( {\overrightarrow {OB'} + \overrightarrow {OD'} } \right)\) \( = \overrightarrow 0 + \overrightarrow 0 + 2\overrightarrow {OO'} + 2\overrightarrow {OO'} = 4\overrightarrow {OO'} \). Suy ra \(OS = \left| {\overrightarrow {OS} } \right| = \left| {4\overrightarrow {OO'} } \right| = 4OO' = 4AA' = 4\frac{{\sqrt 3 }}{{16}} = \frac{{\sqrt 3 }}{4}\). Khi đó a = 1, b = 4. Ta có \(P = {a^2} + {b^2} = {1^2} + {4^2} = 17\).
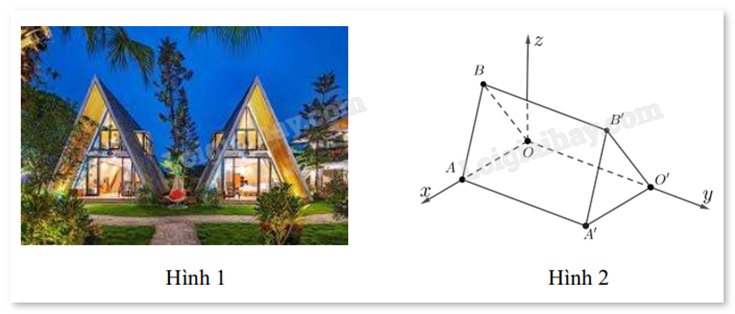
Câu 5 :
Những căn nhà gỗ trong Hình 1 được phác thảo dưới dạng một hình lăng trụ đứng tam giác OAB⋅O′A′B′. Với hệ trục toạ độ Oxyz thể hiện như Hình 2 (đơn vị đo lấy theo centimét), hai điểm A′ và B′ có tọa độ lần lượt là (240;450;0) và̀ (120;450;300). Mỗi căn nhà gỗ có chiều dài là a cm, chiều rộng là b cm, mỗi cạnh bên của mặt tiền có độ dài là c cm. Tính a + b + c (làm tròn đến hàng đơn vị).
Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng quy tắc tính tọa độ vecto, tính độ dài vecto. Lời giải chi tiết :
Ta có: a = AA’, b = A’O’, c = A’B’ = B’O’. Vì A’ có tọa độ (240;450;0) nên khoảng cách từ A’ đến trục Ox, Oy lần lượt là 450 cm và 250 cm. Hay AA’ = 450 cm và A’O’ = 240 cm. Ta có \(\overrightarrow {A'B'} = (120 - 240;450 - 450;300 - 0) = ( - 120;0;300)\). \(A'B' = \left| {\overrightarrow {A'B'} } \right| = \sqrt {{{( - 120)}^2} + {0^2} + {{300}^2}} = 60\sqrt {29} \) (cm). Vì O’O = A’A = 450 cm và O’ nằm trên trục Oy nên O’(0;450;0). \(\overrightarrow {O'B'} = (120 - 0;450 - 450;300 - 0) = (120;0;300)\). \(\left| {\overrightarrow {O'B'} } \right| = \sqrt {{{120}^2} + {0^2} + {{300}^2}} = 60\sqrt {29} \). Vậy a + b + c = 450 + 240 + \(60\sqrt {29} \) \( \approx 1013\).
Câu 6 :
Người ta ghi lại tuổi thọ của một số con ong cho kết quả như sau:
Tính khoảng tứ phân vị của mẫu số liệu (làm tròn kết quả đến hàng phần mười). Đáp án: Đáp án
Đáp án: Phương pháp giải :
Tứ phân vị thứ i, kí hiệu là \({Q_i}\) với i = 1, 2, 3 của mẫu số liệu ghép nhóm được xác định như sau: \({Q_i} = {u_m} + \frac{{\frac{{in}}{4} - C}}{{{n_m}}}({u_{m + 1}} - {u_m})\). Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu. \([{u_m};{u_{m + 1}})\) là nhóm chứa tứ phân vị thứ i. \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ i. \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\). Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\). Lời giải chi tiết :
Cỡ mẫu: n = 5 + 12 + 23 + 31 + 29 = 100. Giả sử tuổi thọ của ong là \({x_1},{x_2},...,{x_{100}}\) được sắp xếp theo thứ tự không giảm. Tứ phân vị thứ nhất là \({Q_1} = 40 + \frac{{\frac{{100}}{4} - (5 + 12)}}{{23}}(60 - 40) = \frac{{1080}}{{23}}\). Tứ phân vị thứ ba là \({Q_3} = 80 + \frac{{\frac{{3.100}}{4} - (5 + 12 + 23 + 31)}}{{29}}(100 - 80) = \frac{{2400}}{{29}}\). Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{2400}}{{29}} - \frac{{1080}}{{23}} \approx 35,8\).
|


























Danh sách bình luận