Đề thi học kì 1 Toán 12 Cánh diều - Đề số 1Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.Đề bài
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Cho hàm số f(x) có bảng biến thiên như hình vẽ dưới đây. Hàm số đồng biến trên khoảng nào trong các khoảng sau?
Câu 4 :
Tổng số đường tiệm cận đứng của đồ thị hàm số \(\frac{1}{{4 - {x^2}}}\) là
Câu 5 :
Cho hàm số \(f(x) = x + 2 - \frac{1}{{x - 1}}\). Tiệm cận xiên của đồ thị đã cho là đường thẳng
Câu 6 :
Cho hàm số f(x) có đạo hàm là \(f'(x) = (x - 4){(x + 1)^2}\). Số cực trị của hàm số f(x) là
Câu 7 :
Trong không gian, cho ba điểm A, B, C phân biệt. Hiệu hai vecto \(\overrightarrow {AB} - \overrightarrow {AC} \) bằng
Câu 8 :
Gọi I là trung điểm của AB. Khẳng định nào sau đây sai?
Câu 9 :
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3). Tọa độ vecto \(\overrightarrow {OA} \) là
Câu 10 :
Trong không gian với hệ trục tọa độ Oxyz, cho hai vecto \(\overrightarrow a = (2;1;0)\) và \(\overrightarrow b = ( - 1;0; - 2)\). Tính \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Câu 11 :
Trong không gian Oxyz, gọi A’ là hình chiếu vuông góc của điểm A(1;2;3) lên mặt phẳng (Oyz). Tọa độ vecto \(\overrightarrow {AA'} \) là
Câu 12 :
Một bác tài xế thống kê lại độ dài quãng đường (đơn vị: km) bác đã lái xe mỗi ngày trong một tháng ở bảng sau:
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Cho hàm số \(f(x) = {x^3} - 6{x^2} - 15x + 20\). a) Đồ thị hàm số y = f(x) cắt trục tung tại điểm có tung độ bằng 20.
Đúng
Sai
b) Hàm số đồng biến trên khoảng \(( - \infty ; - 1) \cap (5; + \infty )\).
Đúng
Sai
c) Giá trị cực đại của hàm số là y = 28.
Đúng
Sai
d) Giá trị nhỏ nhất của hàm số trên khoảng \(( - 4; + \infty )\) bằng –80.
Đúng
Sai
Câu 2 :
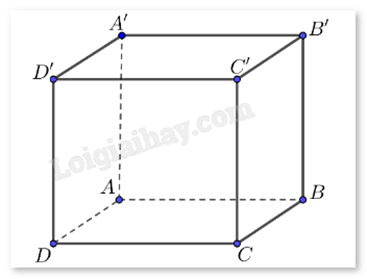
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 2, AD = 3, AA’ = 4. Các mệnh đề sau đúng hay sai? a) \(\overrightarrow {BA'} = \overrightarrow {CD'} \). b) \(\left| {\overrightarrow {BA'} } \right| = \left| {\overrightarrow {A'D} } \right| = \left| {\overrightarrow {DB} } \right|\).
Đúng
Sai
b) \(\left| {\overrightarrow {BA'} } \right| = \left| {\overrightarrow {A'D} } \right| = \left| {\overrightarrow {DB} } \right|\).
Đúng
Sai
c) Số vecto khác \(\overrightarrow 0 \) có điểm đầu và điểm cuối là các đỉnh của hình hộp là \(A_8^2\).
Đúng
Sai
d) \(\left| {\overrightarrow {BD'} } \right| = 3\sqrt 3 \).
Đúng
Sai
Câu 3 :
Trong không gian Oxyz, cho \(\overrightarrow a = (1;2; - 3)\), \(\overrightarrow b = (3;1;5)\). a) \(\overrightarrow a + \overrightarrow b = (4;3;2)\).
Đúng
Sai
b) \(2\overrightarrow a - 3\overrightarrow b = ( - 7;1;21)\).
Đúng
Sai
c) \(\overrightarrow a .\overrightarrow b = 10\).
Đúng
Sai
d) \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - \frac{{\sqrt {10} }}{7}\).
Đúng
Sai
Câu 4 :
Thống kê thời gian dùng Facebook một ngày của các bạn trong lớp 12C được kết quả ghép nhóm như sau:
a) Giá trị đại diện của nhóm thứ nhất theo chiều từ trái sang phải là 5.
Đúng
Sai
b) Thời gian trung bình dùng Facebook của mỗi bạn trong lớp 12C là 12.
Đúng
Sai
c) Phương sai của mẫu số liệu trên gần bằng 80.
Đúng
Sai
d) Độ lệch chuẩn của mẫu số liệu trên là 11.
Đúng
Sai
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
Để thiết kế một chiếc bể cá hình hộp chữ nhật có chiều cao là 60 cm, thể tích 96000 \(c{m^3}\).
Chi phí thấp nhất để hoàn thành bể cá là bao nhiêu VNĐ? Đáp án:
Câu 2 :
Một bác nông dân có 60000000 đồng để làm một cái rào hình chữ E đọc theo một con sông (như hình vẽ) để làm một khu đất có hai phần bằng nhau để trồng cà chua. Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 50000 đồng một mét, còn đối với ba mặt hàng rào song song với nhau thì chi phí nguyên vật liệu là 40000 đồng một mét. Tìm diện tích lớn nhất (\({m^2}\)) của đất có thể rào được?
Đáp án:
Câu 3 :
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị như sau:
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau? i) bd < 0. ii) cd > 0. iii) ac > 0. iv) bc > 0. v) ab < 0. vi) ad < 0. Đáp án:
Câu 4 :
Ba lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) cùng tác động vào một vật. Biết ba lực đó đối nhau tạo với nhau một góc \({120^o}\) và có độ lớn lần lượt là 15 N, 7 N, 12 N. Tính độ lớn hợp lực của ba lực trên. Đáp án:
Câu 5 :
Với hệ trục tọa độ Oxyz sao cho O nằm trên mặt nước, mặt phẳng (Oxy) là mặt nước, trục Oz hướng lên trên (đơn vị đo: mét), một con chim bói cá đang ở vị trí cách mặt nước 2m, cách mặt phẳng (Oxz), (Oyz) lần lượt là 3m và 1m phóng thẳng xuống vị trí con cá, biết con cá cách mặt nước 50cm, cách mặt phẳng (Oxz), (Oyz) lần lượt là 1m và 1,5m. Điểm B là điểm chim bói cá tiếp xúc với mặt nước. Giả sử hoành độ điểm B là a. Tìm 5a.
Đáp án:
Câu 6 :
Khảo sát thời gian đọc sách trong ngày của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau:
Tính khoảng tứ phân vị của mẫu số liệu. Đáp án: Lời giải và đáp án
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
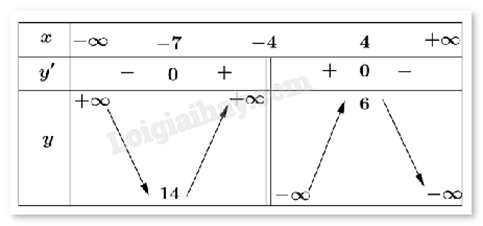
Cho hàm số f(x) có bảng biến thiên như hình vẽ dưới đây. Hàm số đồng biến trên khoảng nào trong các khoảng sau?
Đáp án : B Phương pháp giải :
Quan sát bảng biến thiên và nhận xét. Lời giải chi tiết :
Quan sát bảng biến thiên thấy y’ > 0 trên khoảng (-7;-4) nên hàm số đồng biến trên khoảng (-7;-4).
Đáp án : A Phương pháp giải :
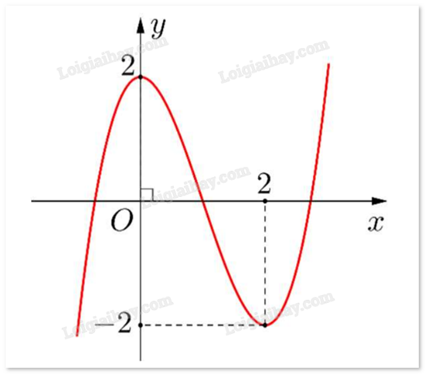
Quan sát đồ thị và nhận xét. Lời giải chi tiết :
Hàm số đạt cực tiểu tại x = 2.
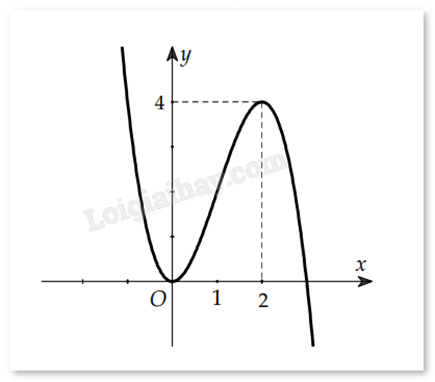
Đáp án : D Phương pháp giải :
Quan sát đồ thị và nhận xét. Lời giải chi tiết :
Hàm số không có giá trị lớn nhất vì \(\mathop {\lim }\limits_{x \to - \infty } f(x) = + \infty \).
Câu 4 :
Tổng số đường tiệm cận đứng của đồ thị hàm số \(\frac{1}{{4 - {x^2}}}\) là
Đáp án : C Phương pháp giải :
\(x = {x_0}\) là tiệm cận đứng của đồ thị f(x) nếu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty \), \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty \), \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty \) hoặc \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \). Lời giải chi tiết :
Ta có \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{1}{{4 - {x^2}}} = - \infty \) và \(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{1}{{4 - {x^2}}} = + \infty \) nên đồ thị hàm số f(x) có hai tiệm cận đứng là x = 2 và x = -2.
Câu 5 :
Cho hàm số \(f(x) = x + 2 - \frac{1}{{x - 1}}\). Tiệm cận xiên của đồ thị đã cho là đường thẳng
Đáp án : B Phương pháp giải :
Đường thẳng y = ax + b là tiệm cận xiên của đồ thị hàm số f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f(x) - (ax + b)} \right] = 0\). Lời giải chi tiết :
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (x + 2)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ {x + 2 - \frac{1}{{x - 1}} - (x + 2)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left( { - \frac{1}{{x - 1}}} \right) = 0\).
Câu 6 :
Cho hàm số f(x) có đạo hàm là \(f'(x) = (x - 4){(x + 1)^2}\). Số cực trị của hàm số f(x) là
Đáp án : B Phương pháp giải :
Hàm số f(x) đạt cực trị tại \({x_0}\) khi \(f'({x_0}) = 0\) và f’(x) đổi dấu khi qua \({x_0}\) (hay \({x_0}\) là nghiệm bội lẻ của \(f'(x) = 0\)). Lời giải chi tiết :
\(f'(x) = (x - 4){(x + 1)^2} = 0\) khi x = 4 hoặc x = -1. Vì f’(x) chỉ đổi dấu khi qua x = 4 (hay x = 4 là nghiệm bội lẻ của \(f'(x) = 0\)) nên hàm số f(x) chỉ có 1 cực trị là x = 4.
Câu 7 :
Trong không gian, cho ba điểm A, B, C phân biệt. Hiệu hai vecto \(\overrightarrow {AB} - \overrightarrow {AC} \) bằng
Đáp án : A Phương pháp giải :
Dựa vào quy tắc ba điểm đối với hiệu của hai vecto. Lời giải chi tiết :
Ta có \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \).
Câu 8 :
Gọi I là trung điểm của AB. Khẳng định nào sau đây sai?
Đáp án : C Phương pháp giải :
Sử dụng tính chất trung điểm. Lời giải chi tiết :
C sai vì \(\overrightarrow {IA} = - \overrightarrow {IB} \) do hai vecto này ngược hướng.
Câu 9 :
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3). Tọa độ vecto \(\overrightarrow {OA} \) là
Đáp án : A Phương pháp giải :
Tọa độ của vecto \(\overrightarrow {OA} \) là tọa độ của A. Lời giải chi tiết :
\(\overrightarrow {OA} = (1;2;3)\).
Câu 10 :
Trong không gian với hệ trục tọa độ Oxyz, cho hai vecto \(\overrightarrow a = (2;1;0)\) và \(\overrightarrow b = ( - 1;0; - 2)\). Tính \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Đáp án : B Phương pháp giải :
Công thức tính góc giữa hai vecto trong không gian: \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\). Lời giải chi tiết :
Ta có: \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{2.( - 1) + 1.0 + 0.( - 2)}}{{\sqrt {{2^2} + {1^2} + {0^2}} .\sqrt {{{( - 1)}^2} + {0^2} + {{( - 2)}^2}} }} = \frac{{ - 2}}{5}\).
Câu 11 :
Trong không gian Oxyz, gọi A’ là hình chiếu vuông góc của điểm A(1;2;3) lên mặt phẳng (Oyz). Tọa độ vecto \(\overrightarrow {AA'} \) là
Đáp án : B Phương pháp giải :
Hình chiếu của điểm M(a;b;c) lên mặt phẳng (Oyz) là điểm M’(0;b;c). Lời giải chi tiết :
Ta có A’(0;2;3) suy ra \(\overrightarrow {AA'} = (0 - 1;2 - 2;3 - 3) = ( - 1;0;0)\).
Câu 12 :
Một bác tài xế thống kê lại độ dài quãng đường (đơn vị: km) bác đã lái xe mỗi ngày trong một tháng ở bảng sau:
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Đáp án : A Phương pháp giải :
Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên chứa dữ liệu. Lời giải chi tiết :
R = 300 – 50 = 250.
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Cho hàm số \(f(x) = {x^3} - 6{x^2} - 15x + 20\). a) Đồ thị hàm số y = f(x) cắt trục tung tại điểm có tung độ bằng 20.
Đúng
Sai
b) Hàm số đồng biến trên khoảng \(( - \infty ; - 1) \cap (5; + \infty )\).
Đúng
Sai
c) Giá trị cực đại của hàm số là y = 28.
Đúng
Sai
d) Giá trị nhỏ nhất của hàm số trên khoảng \(( - 4; + \infty )\) bằng –80.
Đúng
Sai
Đáp án
a) Đồ thị hàm số y = f(x) cắt trục tung tại điểm có tung độ bằng 20.
Đúng
Sai
b) Hàm số đồng biến trên khoảng \(( - \infty ; - 1) \cap (5; + \infty )\).
Đúng
Sai
c) Giá trị cực đại của hàm số là y = 28.
Đúng
Sai
d) Giá trị nhỏ nhất của hàm số trên khoảng \(( - 4; + \infty )\) bằng –80.
Đúng
Sai
Phương pháp giải :
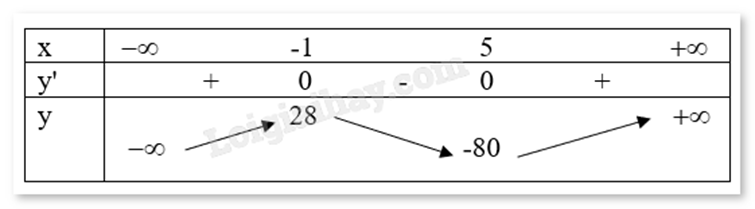
Lập bảng biến thiên và nhận xét. Lời giải chi tiết :
Tập xác định: D = R. Ta có \(f'(x) = 3{x^2} - 12x - 15 = 0 \Leftrightarrow \) x = 5 hoặc x = -1. Bảng biến thiên:
a) Đúng. Đồ thị cắt trục tung tại điểm có hoành độ bằng 0. Thay x = 0 vào hàm số ta được: \(f(0) = {0^3} - {6.0^2} - 15.0 + 20 = 20\). Vậy đồ thị hàm số y = f(x) cắt trục tung tại điểm có tung độ bằng 20. b) Sai. Hàm số đồng biến trên khoảng \(( - \infty ; - 1)\) và \((5; + \infty )\). Dấu “\( \cap \)” là sai. c) Đúng. Giá trị cực đại của hàm số là y = 28 tại x = -1. d) Đúng. Có \(f( - 4) = f(5) = - 80\). Vậy giá trị nhỏ nhất của hàm số trên khoảng \(( - 4; + \infty )\) bằng –80.
Câu 2 :
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 2, AD = 3, AA’ = 4. Các mệnh đề sau đúng hay sai? a) \(\overrightarrow {BA'} = \overrightarrow {CD'} \). b) \(\left| {\overrightarrow {BA'} } \right| = \left| {\overrightarrow {A'D} } \right| = \left| {\overrightarrow {DB} } \right|\).
Đúng
Sai
b) \(\left| {\overrightarrow {BA'} } \right| = \left| {\overrightarrow {A'D} } \right| = \left| {\overrightarrow {DB} } \right|\).
Đúng
Sai
c) Số vecto khác \(\overrightarrow 0 \) có điểm đầu và điểm cuối là các đỉnh của hình hộp là \(A_8^2\).
Đúng
Sai
d) \(\left| {\overrightarrow {BD'} } \right| = 3\sqrt 3 \).
Đúng
Sai
Đáp án
a) \(\overrightarrow {BA'} = \overrightarrow {CD'} \). b) \(\left| {\overrightarrow {BA'} } \right| = \left| {\overrightarrow {A'D} } \right| = \left| {\overrightarrow {DB} } \right|\).
Đúng
Sai
b) \(\left| {\overrightarrow {BA'} } \right| = \left| {\overrightarrow {A'D} } \right| = \left| {\overrightarrow {DB} } \right|\).
Đúng
Sai
c) Số vecto khác \(\overrightarrow 0 \) có điểm đầu và điểm cuối là các đỉnh của hình hộp là \(A_8^2\).
Đúng
Sai
d) \(\left| {\overrightarrow {BD'} } \right| = 3\sqrt 3 \).
Đúng
Sai
Phương pháp giải :
Dựa vào khái niệm vecto, vecto bằng nhau, cách tính độ dài vecto, tính độ dài đường chéo hình hộp. Lời giải chi tiết :
a) Đúng. \(\overrightarrow {BA'} = \overrightarrow {CD'} \) vì chúng cùng hướng và cùng độ dài. b) Sai. Ta có: \(\left| {\overrightarrow {BA'} } \right| = BA' = \sqrt {B{A^2} + BB{'^2}} = \sqrt {{2^2} + {4^2}} = \sqrt {20} \). \(\left| {\overrightarrow {BD} } \right| = BD = \sqrt {B{C^2} + B{A^2}} = \sqrt {{3^2} + {2^2}} = \sqrt {13} \). Vậy \(\left| {\overrightarrow {BA'} } \right| \ne \left| {\overrightarrow {BD} } \right|\). c) Đúng. Số đỉnh của hình hộp là 8. Mỗi vecto khác \(\overrightarrow 0 \) được tạo thành từ 2 điểm phân biệt trong 8 điểm đỉnh. Mỗi 2 điểm lại tạo thành 2 vecto khác nhau (cùng độ dài, ngược hướng). Vậy có \(A_8^2\) vecto được tạo thành. d) Sai. \(\left| {\overrightarrow {BD'} } \right| = \sqrt {B{A^2} + B{C^2} + BB{'^2}} = \sqrt {4 + 9 + 16} = \sqrt {29} \).
Câu 3 :
Trong không gian Oxyz, cho \(\overrightarrow a = (1;2; - 3)\), \(\overrightarrow b = (3;1;5)\). a) \(\overrightarrow a + \overrightarrow b = (4;3;2)\).
Đúng
Sai
b) \(2\overrightarrow a - 3\overrightarrow b = ( - 7;1;21)\).
Đúng
Sai
c) \(\overrightarrow a .\overrightarrow b = 10\).
Đúng
Sai
d) \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - \frac{{\sqrt {10} }}{7}\).
Đúng
Sai
Đáp án
a) \(\overrightarrow a + \overrightarrow b = (4;3;2)\).
Đúng
Sai
b) \(2\overrightarrow a - 3\overrightarrow b = ( - 7;1;21)\).
Đúng
Sai
c) \(\overrightarrow a .\overrightarrow b = 10\).
Đúng
Sai
d) \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - \frac{{\sqrt {10} }}{7}\).
Đúng
Sai
Phương pháp giải :
Sử dụng các quy tắc cộng, trừ vecto, nhân vecto với một số, tích vô hướng của hai vecto. Lời giải chi tiết :
a) Đúng. \(\overrightarrow a + \overrightarrow b = (1 + 3;2 + 1; - 3 + 5) = (4;3;2)\). b) Sai. \(2\overrightarrow a - 3\overrightarrow b = (2.1 - 3.3;2.2 - 3.1;2.( - 3) - 3.5) = ( - 7;1; - 21)\). c) Sai. \(\overrightarrow a .\overrightarrow b = 1.3 + 2.1 - 3.5 = - 10\). d) Đúng. \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{ - 10}}{{\sqrt {{1^2} + {2^2} + {{( - 3)}^2}} .\sqrt {{3^2} + {1^2} + {5^2}} }} = - \frac{{\sqrt {10} }}{7}\).
Câu 4 :
Thống kê thời gian dùng Facebook một ngày của các bạn trong lớp 12C được kết quả ghép nhóm như sau:
a) Giá trị đại diện của nhóm thứ nhất theo chiều từ trái sang phải là 5.
Đúng
Sai
b) Thời gian trung bình dùng Facebook của mỗi bạn trong lớp 12C là 12.
Đúng
Sai
c) Phương sai của mẫu số liệu trên gần bằng 80.
Đúng
Sai
d) Độ lệch chuẩn của mẫu số liệu trên là 11.
Đúng
Sai
Đáp án
a) Giá trị đại diện của nhóm thứ nhất theo chiều từ trái sang phải là 5.
Đúng
Sai
b) Thời gian trung bình dùng Facebook của mỗi bạn trong lớp 12C là 12.
Đúng
Sai
c) Phương sai của mẫu số liệu trên gần bằng 80.
Đúng
Sai
d) Độ lệch chuẩn của mẫu số liệu trên là 11.
Đúng
Sai
Phương pháp giải :
a) \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) với i = 1, 2,…, k là giá trị đại diện cho nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\). b) Số trung bình: \(\bar x{\rm{\;}} = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\). c) Phương sai: \({s^2} = \frac{{m{{({x_1} - \bar x)}^2} + ... + {m_k}{{({x_k} - \bar x)}^2}}}{n}\). d) Độ lệch chuẩn: \(s = \sqrt {{s^2}} \). Lời giải chi tiết :
a) Đúng. Giá trị đại diện của nhóm thứ nhất là \(\frac{{0 + 10}}{2} = 5\). b) Sai. Thời gian trung bình dùng Facebook của mỗi bạn trong lớp 12C là: \(\overline x = \frac{{5.15 + 15.10 + 25.5 + 35.2}}{{15 + 10 + 5 + 2}} = 13,125\) (phút). c) Sai. Phương sai của mẫu số liệu trên là: \({s^2} = \frac{{15.{{(5 - 13,125)}^2} + 10.{{(15 - 13,125)}^2} + 5.{{(25 - 13,125)}^2} + 2.{{(35 - 13,125)}^2}}}{{15 + 10 + 5 + 2}} = \frac{{5375}}{{64}} \approx 84\). d) Sai. Độ lệch chuẩn của mẫu số liệu trên là \(s = \frac{{5\sqrt {215} }}{8} \approx 9,16\).
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
Để thiết kế một chiếc bể cá hình hộp chữ nhật có chiều cao là 60 cm, thể tích 96000 \(c{m^3}\).
Chi phí thấp nhất để hoàn thành bể cá là bao nhiêu VNĐ? Đáp án: Đáp án
Đáp án: Phương pháp giải :
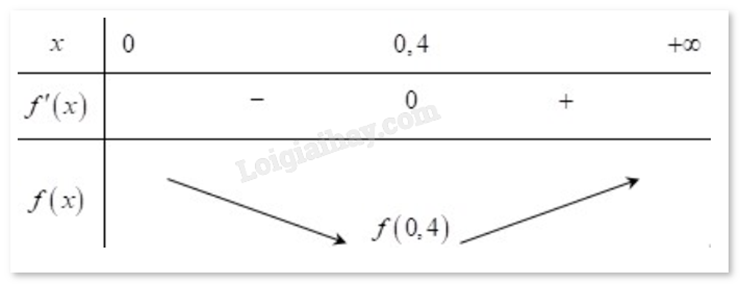
Thay x = 0,4 vào hàm số f(x) và tính kết quả. Lời giải chi tiết :
Theo bảng biến thiên, giá thành của bể cá là f(x) đạt giá trị nhỏ nhất tại x = 0,4. Ta có \(f(0,4) = 2.0,6\left( {0,4 + \frac{{0,16}}{{0,4}}} \right).700000 + 1000000.0,4.\frac{{0,16}}{{0,4}} = 832000\) (VNĐ). Vậy chi phí thấp nhất để hoàn thành bể cá là 832000 VNĐ.
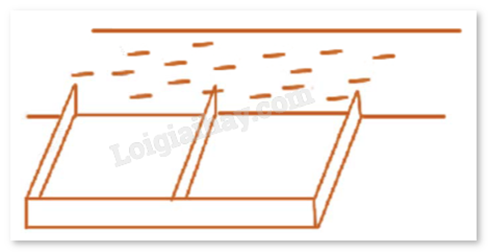
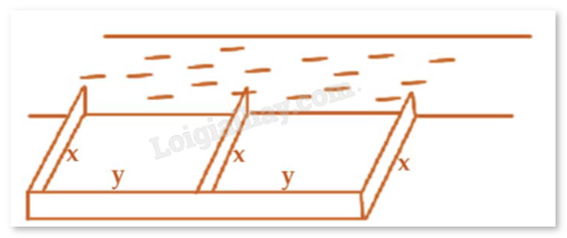
Câu 2 :
Một bác nông dân có 60000000 đồng để làm một cái rào hình chữ E đọc theo một con sông (như hình vẽ) để làm một khu đất có hai phần bằng nhau để trồng cà chua. Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 50000 đồng một mét, còn đối với ba mặt hàng rào song song với nhau thì chi phí nguyên vật liệu là 40000 đồng một mét. Tìm diện tích lớn nhất (\({m^2}\)) của đất có thể rào được?
Đáp án: Đáp án
Đáp án: Phương pháp giải :
Lập hàm số biểu diễn diện tích mảnh đất và tìm giá trị lớn nhất của hàm số đó. Lời giải chi tiết :
Gọi chiều dài mỗi mặt rào vuông góc với bờ là x (mét, x > 0). Chiều dài mặt rào song song với bờ là 2y (mét, y > 0). Chi phí mua rào vuông góc với bờ là 40000.3x = 120000x (đồng). Chi phí mua rào song song với bờ là 50000.2y = 100000y (đồng). Tồng chi phí bác nông dân có thể bỏ ra là 60000000 đồng nên ta có: \(120000x + 100000y = 60000000 \Leftrightarrow 6x + 5y = 3000 \Leftrightarrow y = 600 - \frac{6}{5}x\). Điều kiện: \(y > 0 \Leftrightarrow 600 - \frac{6}{5}x > 0 \Leftrightarrow x < 500\). Diện tích khu đất rào được là: \(S = 2xy = 2x\left( {600 - \frac{6}{5}x} \right) = 1200x - \frac{{12}}{5}{x^2}\). Xét hàm số \(f(x) = 1200x - \frac{{12}}{5}{x^2}\) với \(x \in (0;500)\). \(f'(x) = 1200 - \frac{{24}}{5}x = 0 \Leftrightarrow x = 250 \in (0;500)\). Ta có: \(f(0) = 0\); \(f(250) = 150000\); \(f(500) = 0\). Suy ra giá trị lớn nhất của hàm số \(f(x) = 1200x - \frac{{12}}{5}{x^2}\) với \(x \in (0;500)\) là 150000 (\({m^2}\)). Vậy diện tích lớn nhất của khu đất rào được là 150000 (\({m^2}\)).
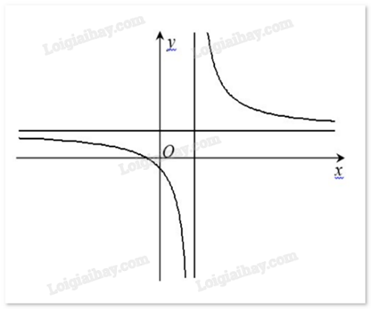
Câu 3 :
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị như sau:
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau? i) bd < 0. ii) cd > 0. iii) ac > 0. iv) bc > 0. v) ab < 0. vi) ad < 0. Đáp án: Đáp án
Đáp án: Phương pháp giải :
Xét dấu ac dựa vào tung độ của tiệm cận ngang. Xét dấu cd dựa vào hoành độ của tiệm cận đứng. Xét dấu bd dựa vào giao của đồ thị với trục tung. Lời giải chi tiết :
Đồ thị cắt trục tung tại điểm có tung độ âm nên \(\frac{b}{d} < 0\) hay \(bd < 0\). Vậy i) đúng. Tiệm cận đứng \(x = - \frac{d}{c}\) có hoành độ dương nên \(x = - \frac{d}{c} > 0\) hay \(cd < 0\). Vậy ii) sai. Tiệm cận ngang \(y = \frac{a}{c}\) có tung độ dương nên \(y = \frac{a}{c} > 0\) hay \(ac > 0\). Vậy iii) đúng. Vì \(\left\{ \begin{array}{l}bd < 0\\cd < 0\end{array} \right.\) suy ra \(bc > 0\). Vậy iv) đúng. Vì \(\left\{ \begin{array}{l}bc > 0\\ac > 0\end{array} \right.\) suy ra \(ab > 0\). Vậy v) sai. Vì \(\left\{ \begin{array}{l}bd < 0\\ab > 0\end{array} \right.\) suy ra \(ad < 0\). Vậy vi) đúng. Vậy chỉ có ii) và vi) sai.
Câu 4 :
Ba lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) cùng tác động vào một vật. Biết ba lực đó đối nhau tạo với nhau một góc \({120^o}\) và có độ lớn lần lượt là 15 N, 7 N, 12 N. Tính độ lớn hợp lực của ba lực trên. Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng quy tắc tổng hợp lực, định lý cos trong tam giác. Lời giải chi tiết :
Vẽ \(\overrightarrow {OA} = \overrightarrow {{F_1}} \), \(\overrightarrow {OB} = \overrightarrow {{F_2}} \), \(\overrightarrow {OC} = \overrightarrow {{F_3}} \). Vẽ hình bình hành OADB và hình bình hành ODEC. Hợp lực tác động vào vật là \(\overrightarrow F = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OD} + \overrightarrow {OC} = \overrightarrow {OE} \) (quy tắc hình bình hành). Xét hình bình hành OADB: \(OD = \sqrt {O{A^2} + O{B^2} + 2.OA.OB.\cos AOB} = \sqrt {{7^2} + {{15}^2} + 2.15.7.\cos {{120}^o}} = 13\). Ta có: \(\overrightarrow {CO} .\overrightarrow {CE} = - \overrightarrow {OC} .\overrightarrow {OD} \) \( = - \overrightarrow {OC} .\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = - \overrightarrow {OC} .\overrightarrow {OA} - \overrightarrow {OC} .\overrightarrow {OB} \) \( = - OC.OA.\cos \widehat {AOC} - OC.OB.\cos \widehat {BOC}\) \( = - 12.15.\cos {120^o} - 12.7.\cos {120^o} = 132\) (sử dụng định lý cos trong tam giác AOC và BOC). Khi đó \(\cos \widehat {OCE} = \cos \left( {\overrightarrow {CO} ,\overrightarrow {CE} } \right) \) \(= \frac{{\overrightarrow {CO} .\overrightarrow {CE} }}{{\left| {\overrightarrow {CO} } \right|.\left| {\overrightarrow {CE} } \right|}} = \frac{{132}}{{12.13}} = \frac{{11}}{{13}}\). Sử dụng định lý cos trong tam giác OEC có: \(OE = \sqrt {C{O^2} + C{E^2} - 2.CO.CE.\cos \widehat {OCE}} \) \(= \sqrt {{{12}^2} + {{13}^2} - 2.12.13.\frac{{11}}{{13}}} = 7\). Vậy độ lớn hợp lực \(\overrightarrow F = \overrightarrow {OE} \) bằng 7 N.
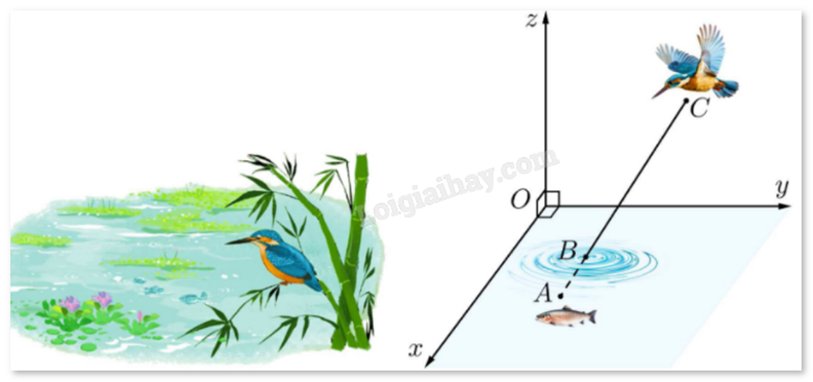
Câu 5 :
Với hệ trục tọa độ Oxyz sao cho O nằm trên mặt nước, mặt phẳng (Oxy) là mặt nước, trục Oz hướng lên trên (đơn vị đo: mét), một con chim bói cá đang ở vị trí cách mặt nước 2m, cách mặt phẳng (Oxz), (Oyz) lần lượt là 3m và 1m phóng thẳng xuống vị trí con cá, biết con cá cách mặt nước 50cm, cách mặt phẳng (Oxz), (Oyz) lần lượt là 1m và 1,5m. Điểm B là điểm chim bói cá tiếp xúc với mặt nước. Giả sử hoành độ điểm B là a. Tìm 5a.
Đáp án: Đáp án
Đáp án: Phương pháp giải :
Tìm tọa độ A, C dựa vào khoảng cách của chúng đến các mặt phẳng tọa độ. Tìm B dựa vào lý thuyết vecto cùng phương. Lời giải chi tiết :
Ta có: A(1,5; 1; -0,5) và C(1; 3; 2), suy ra \(\overrightarrow {AC} = ( - 0,5;2;2,5)\). Vì B thuộc mặt phẳng (Oxy) nên \(B({x_B};{y_B};0)\). \(\overrightarrow {BC} = (1 - {x_B};3 - {y_B};2 - 0) = (1 - {x_B};3 - {y_B};2)\). Vì A, B, C thẳng hàng và B nằm giữa A, C nên \(\overrightarrow {AC} = k\overrightarrow {BC} \) hay \(\left\{ \begin{array}{l}k(1 - {x_B}) = - 0,5\\k(3 - {y_B}) = 2\\2k = 2,5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k = \frac{5}{4}\\{x_B} = \frac{7}{5}\\{y_B} = \frac{7}{5}\end{array} \right.\). Vậy \(a = \frac{7}{5}\) suy ra 5a = 7.
Câu 6 :
Khảo sát thời gian đọc sách trong ngày của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau:
Tính khoảng tứ phân vị của mẫu số liệu. Đáp án: Đáp án
Đáp án: Phương pháp giải :
Công thức: \({\Delta _Q} = {Q_3} - {Q_1}\). Lời giải chi tiết :
Cỡ mẫu: n = 4 + 6 + 15 + 12 + 3 = 40. Do \(\frac{n}{4} = 10\) nên \({Q_1} = 60\). Do \(\frac{{3n}}{4} = 30\) nên nhóm chứa \({Q_3}\) là [90;120). \({Q_3} = 90 + \frac{{\frac{{3.40}}{4} - (4 + 6 + 15)}}{{12}}(120 - 90) = 102,5\). Vậy \({\Delta _Q} = {Q_3} - {Q_1} = 102,5 - 60 = 42,5\).
|























Danh sách bình luận