Đề thi học kì 1 môn toán lớp 7 năm 2019 - 2020 trường THCS Dịch Vọng

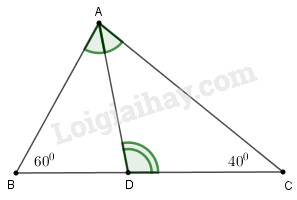
I. TRẮC NGHIỆM (2 điểm). Ghi lại chữ cái đứng trước câu trả lời đúng.

Câu 1. Kết quả thực hiện phép tính ${\left( { - 0,5} \right)^2} + \dfrac{3}{4}$ là

A. $\dfrac{1}{4}$                                                 B. $1$

C. $\dfrac{{ - 1}}{2}$                                             D. $\dfrac{1}{2}$

Câu 2. Kết quả thực hiện phép tính $\dfrac{{ - 3}}{8} + \dfrac{1}{4}:2$ là

A. $\dfrac{1}{4}$                                               B. $\dfrac{{ - 1}}{{16}}$

C. $\dfrac{{ - 1}}{4}$                                            D. $\dfrac{1}{2}$

Câu 3. Cho $\Delta ABC$ có $\widehat A = 50^\circ ,\,\,\widehat C = 70^\circ$. Góc ngoài của tam giác tại đỉnh $B$ có số đo là

A. $140^\circ$                                          B. $100^\circ$

C. $60^\circ$                                            D. $120^\circ$

Câu 4. Cho hình vẽ sau. Biết $AD$ là tia phân giác $\widehat {BAC}$. Tính số đo $\widehat {ADC}$.

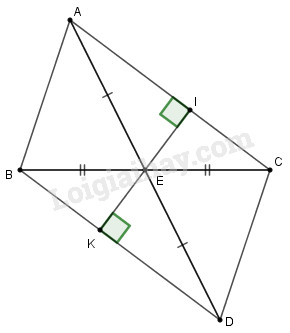
A. $100^\circ$                                          B. $80^\circ$

C. $120^\circ$                                          D. $110^\circ$

II. TỰ LUẬN (8 điểm).

Bài 1 (1 điểm). Thực hiện phép tính:

$a)\,\,\dfrac{2}{5}.15\dfrac{1}{3} - \dfrac{2}{5}.10\dfrac{1}{3}$                                               $b)\,\,{\left( { - \dfrac{2}{3}} \right)^0} - \dfrac{1}{5}:\sqrt {\dfrac{9}{{25}}}  + 20\%$  

Bài 2 (1 điểm). Tìm $x$, biết:

$a)\,\,{\left( {x - 1} \right)^3} =  - 27$                                               $b)\,\,2 - \dfrac{1}{2}\left| {2x - 1} \right| = 0,5$  

Bài 3 (1 điểm). Cho hàm số $y = f\left( x \right) = 2x + 1$

a) Tính $f\left( {\dfrac{1}{2}} \right)$.

b) Tính giá trị của $x$ tại $y =  - 1$.

Bài 4 (1,5 điểm). Ba đội máy cày, cày trên ba cánh đồng có diện tích như nhau. Đội một hoàn thành công việc trong $4$  ngày, đội hai hoàn thành công việc trong $6$ ngày, đội ba hoàn thành công việc trong $8$ ngày. Hỏi mỗi đội có bao nhiêu máy cày, biết đội một nhiều hơn đội hai $6$máy và năng suất các máy như nhau.

Bài 5 (3 điểm). Cho $\Delta ABC$, $E$ là trung điểm của $BC$. Lấy $D$ thuộc tia đối của tia $EA$ sao cho $ED = EA$.

a) Chứng minh rằng: $\Delta AEB = \Delta DEC$.

b) Chứng minh rằng: $AC//BD$.

c) Kẻ $EI \bot AC\,\,\left( {I \in AC} \right);$ $EK \bot BD\,\,\left( {K \in BD} \right)$. Chứng minh $\Delta AIE = \Delta DKE$.

d) Chứng minh $3$ điểm $I,E,K$ thẳng hàng.

Bài 6 (0,5 điểm). Tìm các số $a,b$ biết:

${\left| {5a - 6b + 300} \right|^{2011}} + {\left( {2a - 3b} \right)^{2010}} = 0$

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiaihay.com

I. TRẮC NGHIỆM

Câu 1 (VD):

Phương pháp:

Thứ tự thực hiện các phép tính đối với biểu thức không có dấu ngoặc:

                        Lũy thừa $\to$  Nhân và chia $\to$ Cộng và trừ

Cách giải:

${\left( { - 0,5} \right)^2} + \dfrac{3}{4} = {\left( {\dfrac{{ - 1}}{2}} \right)^2} + \dfrac{3}{4}$ $= \dfrac{1}{4} + \dfrac{3}{4} = \dfrac{4}{4} = 1$

Chọn B

Câu 2 (VD):

Phương pháp:

Thứ tự thực hiện các phép tính đối với biểu thức không có dấu ngoặc:

                        Lũy thừa $\to$ Nhân và chia $\to$ Cộng và trừ

Cách giải:

$\dfrac{{ - 3}}{8} + \dfrac{1}{4}:2 = \dfrac{{ - 3}}{8} + \dfrac{1}{{4.2}}$$= \dfrac{{ - 3}}{8} + \dfrac{1}{8} = \dfrac{{ - 2}}{8} = \dfrac{{ - 1}}{4}$

Chọn C

Câu 3 (VD):

Phương pháp:

- Áp dụng định lí tổng ba góc trong tam giác để tìm tổng số đo góc $B$.

- Áp dụng tính chất : Hai góc kề bù có tổng số đo bằng $180^\circ$.

Cách giải:

Áp dụng định lí tổng ba góc trong tam giác $ABC$ ta có:

$\widehat A + \widehat B + \widehat C = 180^\circ$

$\Rightarrow \widehat B = 180^\circ  - \left( {\widehat A + \widehat C} \right)$$= 180^\circ  - \left( {50^\circ  + 70^\circ } \right) = 60^\circ$

Vì góc ngoài tại đỉnh $B$ và góc $B$ là hai góc kề bù nên có tổng số đo là $180^\circ$.

Suy ra góc ngoài của tam giác tại đỉnh $B$ có số đo là $180^\circ  - 60^\circ  = 120^\circ$.

Chọn D

Câu 4 (VD):

Phương pháp:

- Áp dụng định lý tổng ba góc trong tam giác : Tổng ba góc trong tam giác bằng $180^\circ$.

- Áp dụng tính chất tia phân giác.

Cách giải:

Áp dụng định lí tổng ba góc trong tam giác $ABC$ ta có:

$\widehat A + \widehat B + \widehat C = 180^\circ$

$\Rightarrow \widehat A = 180^\circ  - \left( {\widehat B + \widehat C} \right)$$= 180^\circ  - \left( {60^\circ  + 40^\circ } \right) = 80^\circ$

Vì $AD$ là tia phân giác $\widehat {BAC}$nên  $\widehat {CAD} = \dfrac{1}{2}\widehat {BAC} = \dfrac{1}{2}.80^\circ  = 40^\circ$.

Áp dụng định lí tổng ba góc trong tam giác $ADC$ ta có:

$\widehat {ADC} + \widehat {DCA} + \widehat {CAD} = 180^\circ$

$\Rightarrow \widehat {ADC} = 180^\circ  - \left( {\widehat {DCA} + \widehat {CAD}} \right)$$= 180^\circ  - \left( {40^\circ  + 40^\circ } \right) = 100^\circ$

Chọn A

II. TỰ LUẬN

Bài 1 (VD):

Phương pháp:

Thứ tự thực hiện các phép tính đối với biểu thức không có dấu ngoặc:

                        Lũy thừa $\to$ Nhân và chia $\to$ Cộng và trừ

Sử dụng tính chất phân phối của phép nhân đối với phép cộng, phép trừ

Cách giải:

$\begin{array}{l}a)\,\,\dfrac{2}{5}.15\dfrac{1}{3} - \dfrac{2}{5}.10\dfrac{1}{3}\\ = \dfrac{2}{5}.\dfrac{{46}}{3} - \dfrac{2}{5}.\dfrac{{31}}{3}\\ = \dfrac{2}{5}.\left( {\dfrac{{46}}{3} - \dfrac{{31}}{3}} \right)\\ = \dfrac{2}{5}.\dfrac{{15}}{3} = 2\end{array}$

$\begin{array}{l}b)\,\,{\left( { - \dfrac{2}{3}} \right)^0} - \dfrac{1}{5}:\sqrt {\dfrac{9}{{25}}}  + 20\% \\ = 1 - \dfrac{1}{5}:\dfrac{3}{5} + \dfrac{1}{5}\\ = 1 - \dfrac{1}{5}.\dfrac{5}{3} + \dfrac{1}{5}\\ = 1 - \dfrac{1}{3} + \dfrac{1}{5}\\ = \dfrac{2}{3} + \dfrac{1}{5}\\ = \dfrac{{13}}{{15}}\end{array}$

Bài 2 (VD):

Phương pháp:

a) Biến đổi $- 27 = {\left( { - 3} \right)^3}$ , sau đó áp dụng tính chất ${A^3} = {B^3} \Rightarrow A = B$  từ đó tìm $x$.

b) Áp dụng quy tắc chuyển vế tìm được $\left| {2x - 1} \right|$, sau đó áp dụng tính chất : $|A| = B \Rightarrow A = B$ hoặc $A =  - B$.

Cách giải:

$\begin{array}{l}a)\,\,{\left( {x - 1} \right)^3} =  - 27\\\,\,\,\,\,\,\,{\left( {x - 1} \right)^3} = {\left( { - 3} \right)^3}\\\,\,\,\,\,\,\,x - 1 =  - 3\\\,\,\,\,\,\,\,x =  - 3 + 1\\\,\,\,\,\,\,\,x =  - 2\end{array}$

Vậy $x =  - 2$ .

$\begin{array}{l}b)\,\,2 - \dfrac{1}{2}\left| {2x - 1} \right| = 0,5\\\,\,\,\,\,\,\,2 - \dfrac{1}{2}\left| {2x - 1} \right| = \dfrac{1}{2}\\\,\,\,\,\,\,\,\dfrac{1}{2}\left| {2x - 1} \right| = 2 - \dfrac{1}{2}\\\,\,\,\,\,\,\,\dfrac{1}{2}\left| {2x - 1} \right| = \dfrac{3}{2}\\\,\,\,\,\,\,\,\left| {2x - 1} \right| = \dfrac{3}{2}:\dfrac{1}{2}\\\,\,\,\,\,\,\,\left| {2x - 1} \right| = 3\end{array}$

$\Rightarrow 2x - 1 = 3$ hoặc $2x - 1 =  - 3$

$\Rightarrow x = 2$ hoặc $x =  - 1$

Vậy $x = 2$ hoặc $x =  - 1$.

Bài 3 (VD):

Phương pháp:

a) Thay giá trị $x = \dfrac{1}{2}$ vào $f\left( x \right)$ rồi tính giá trị tương ứng của $y$.

b) Thay giá trị của $y$ vào biểu thức rồi tìm giá trị tương ứng của $x$ .

Cách giải:

a) Tính $f\left( {\dfrac{1}{2}} \right)$.

Thay $x = \dfrac{1}{2}$ vào hàm số $y = f\left( x \right) = 2x + 1$ ta được:

$f\left( {\dfrac{1}{2}} \right) = 2.\dfrac{1}{2} + 1 = 1 + 2 = 2$.

b) Tính giá trị của $x$ tại $y =  - 1$.

Với$y =  - 1$ ta có : $2x + 1 =  - 1 \Leftrightarrow 2x =  - 2 \Leftrightarrow x =  - 1$.

Bài 4 (VD): 

Phương pháp:

- Áp dụng tính chất của hai đại lượng tỉ lệ nghịch.

- Áp dụng tính chất của dãy tỉ số bằng nhau.

Cách giải:

Gọi số máy của ba đội lần lượt là $a,b,c\,\,\left( {a,b,c \in {\mathbb{N}^*}} \right)$.

Vì trong cùng một cánh đồng số máy và thời gian hoàn thành là hai đại lượng tỉ lệ nghịch nên: $a.4 = b.6 = c.8 = k\;$.

Ta có $a.4 = b.6 \Rightarrow \dfrac{a}{6} = \dfrac{b}{4}$ và $a - b = 6$

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

$\begin{array}{l}\dfrac{a}{6} = \dfrac{b}{4} = \dfrac{{a - b}}{{6 - 4}} = \dfrac{6}{2} = 3\\ + )\,\,\dfrac{a}{6} = 3 \Rightarrow a = 3.6 = 18\,\,\left( {tmdk} \right)\\ + )\,\,\dfrac{b}{4} = 3 \Rightarrow b = 3.4 = 12\,\,\left( {tmdk} \right)\end{array}$

Vì $b.6 = c.8$$\Rightarrow c = \dfrac{{b.6}}{8} = \dfrac{{12.6}}{8} = 9\,\,\left( {tmdk} \right)$

Vậy số máy của đội 1, đội 2 và đội 3 lần lượt là $18\,;\,\,12\,;\,\,9$ máy.

Bài 5 (VD):

b) Chứng minh rằng: $AC//BD$.

c) KẺ $EI \bot AC\,\,\left( {I \in AC} \right);$ $EK \bot BD\,\,\left( {K \in BD} \right)$. Chứng minh $\Delta AIE = \Delta DKE$.

d) Chứng minh $3$ điểm $I,E,K$ thẳng hàng.

Phương pháp:

Áp dụng các trường hợp bằng nhau của tam giác và các tính chất của hai tam giác bằng nhau.

Cách giải:

Cho $\Delta ABC$, $E$ là trung điểm của $BC$. Lấy $D$ thuộc tia đối của tia $EA$ sao cho $ED = EA$. 

a) Chứng minh rằng: $\Delta AEB = \Delta DEC$.

Xét hai tam giác $AEB$ và $DEC$ có:

$BE = EC\,\,\left( {gt} \right)$

$\widehat {AEB} = \widehat {DEC}$ (2 góc đối đỉnh)

$EA = ED\,\,(gt)$

Vậy $\Delta AEB = \Delta DEC\,\,\left( {c.g.c} \right)$

b) Chứng minh rằng: $AC//BD$.

Xét hai tam giác $AEC$ và $DEB$ có:

$BE = EC\,\,\left( {gt} \right)$

$\widehat {AEC} = \widehat {DEB}$ (2 góc đối đỉnh)

$EA = ED\,\,(gt)$

Vậy $\Delta AEC = \Delta DEB\,\,\left( {c.g.c} \right)$

$\Rightarrow \widehat {CAE} = \widehat {BDE}$ (2 góc tương ứng)

Mà hai góc $CAE$ và góc $BDE$ là hai góc so le trong, suy ra $AC//BD$.

c) Kẻ $EI \bot AC\,\,\left( {I \in AC} \right);$ $EK \bot BD\,\,\left( {K \in BD} \right)$. Chứng minh $\Delta AIE = \Delta DKE$.

Xét hai tam giác vuông $AIE$ và $DKE$ có: 

$EA = ED\,\,\left( {gt} \right)$

$\widehat I = \widehat K = 90^\circ \,\,\left( {gt} \right)$

$\Rightarrow \widehat {IAE} = \widehat {KDE}$ (cm câu b)

Vậy $\Delta AIE = \Delta DKE$ (cạnh huyền – góc nhọn).

d) Chứng minh $3$ điểm $I,E,K$ thẳng hàng.

Vì $AC//BD$ (theo câu b) mà $IE \bot AC$ nên $IE \bot BD$

Lại có $EK \bot BD\left( {gt} \right)$ nên $E;I;K$ cùng thuộc một đường thẳng.

Hay $E,I,K$ thẳng hàng.

Bài 5 (VDC):

Phương pháp:

Áp dụng tính chất : $\left| x \right| \ge 0$ với mọi $x \in Z$ và ${x^n} \ge 0$ với mọi $n$ là số chẵn.

Cách giải: 

${{{\left| {5a - 6b + 300} \right|}^{2011}} + {{\left( {2a - 3b} \right)}^{2010}} = 0}$

${\left| {5a - 6b + 300} \right|^{2011}} \ge 0$

${{{\left( {2a - 3b} \right)}^{2010}} \ge 0}$

$\Rightarrow {{\left| {5a - 6b + 300} \right|}^{2011}} + {{\left( {2a - 3b} \right)}^{2010}}$$\ge 0$

$Hay\,\,{{\left| {5a - 6b + 300} \right|}^{2011}}$$+ {{\left( {2a - 3b} \right)}^{2010}} = 0$

${khi\left\{ {\begin{array}{*{20}{l}}{5a - 6b + 300 = 0}\\{2a - 3b = 0}\end{array}} \right.}$

${2a - 3b = 0 \Rightarrow 2a = 3b}$

$\Rightarrow \dfrac{a}{3} = \dfrac{b}{2} = \dfrac{{5a - 6b}}{{3.5 - 2.6}}$$= \dfrac{{ - 300}}{3} =  - 100$

${ \Rightarrow a =  - 300;b =  - 200}$

HẾT

Loigiaihay.com