Đề thi giữa kì 1 Toán 12 - Đề số 3Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số y = f(x) xác định trên R{-1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình. Mệnh đề nào dưới đây đúng?Đề bài
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
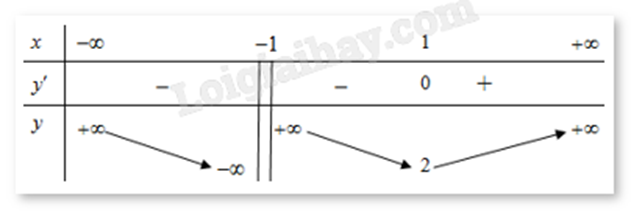
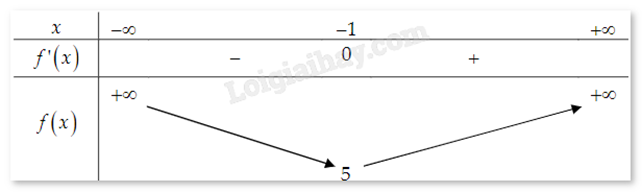
Cho hàm số y = f(x) xác định trên R\{-1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình. Mệnh đề nào dưới đây đúng?
Câu 2 :
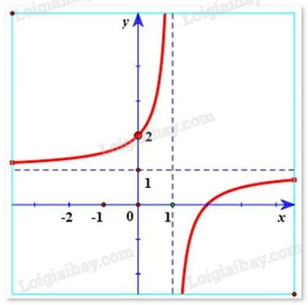
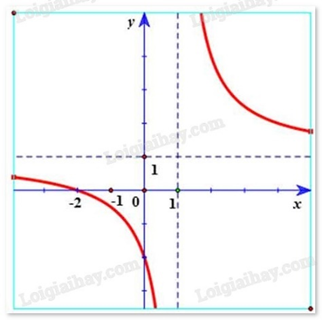
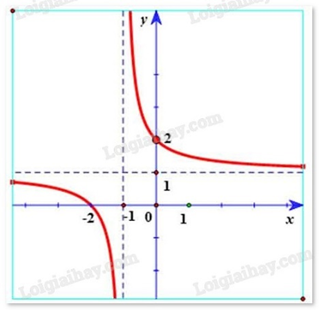
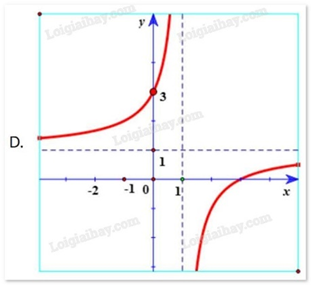
Hàm số \(y = \frac{{x - 2}}{{x - 1}}\) có đồ thị là hình vẽ nào sau đây? Hãy chọn câu trả lời đúng.
Câu 3 :
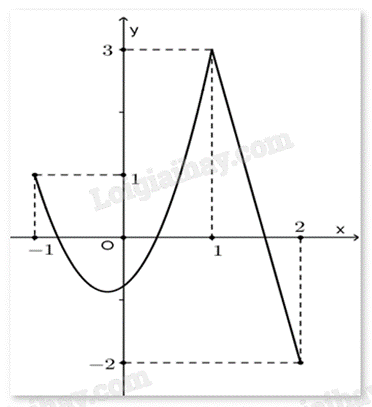
Cho hàm số y = f(x) liên tục trên đoạn [–1;2] và có đồ thị như hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [–1;2]. Tính M + 2m.
Câu 4 :
Cho hàm số y = f(x) có bảng biến thiên như sau:
Tổng số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số đã cho là:
Câu 5 :
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 4x - 7}}{{x - 2}}\) là:
Câu 6 :
Tọa độ tâm đối xứng của đồ thị hàm số \(y = \frac{{x + 4}}{{x - 3}}\) là:
Câu 7 :
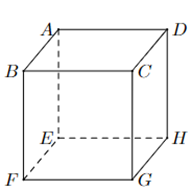
Cho hình hộp ABCD.EFGH. Kết quả phép toán \(\overrightarrow {AB} - \overrightarrow {EH} \) là
Câu 9 :
Giá trị lớn nhất của hàm số \(y = \sqrt {25 - {x^2}} \) trên đoạn [-4;4] là:
Câu 10 :
Cho hàm số y = f(x) có đạo hàm \(f'(x) = x(x - 2)({x^2} - 4)(x + 1)\). Hàm số y = f(x) có bao nhiêu điểm cực trị?
Câu 11 :
Trong không gian với hệ tọa độ Oxyz, cho vecto \(\overrightarrow u = 2\overrightarrow j + 3\overrightarrow i - \overrightarrow k \). Tọa độ của vecto \(\overrightarrow u \) là
Câu 12 :
Cho hai vecto \(\overrightarrow u = (2; - 1;3)\), \(\overrightarrow v = ( - 3;4;1)\). Tích \(\overrightarrow u .\overrightarrow v \) bằng:
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
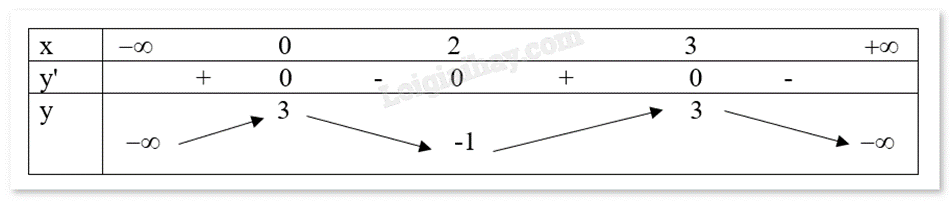
a) Hàm số f(x) đồng biến trên mỗi khoảng (0;2) và (2;3)
Đúng
Sai
b) Số điểm cực trị của hàm số đã cho là 3
Đúng
Sai
c) Hàm số f(x) có giá trị lớn nhất bằng 3
Đúng
Sai
Hàm số đạt cực tiểu tại x = -1 d) Hàm số đạt cực tiểu tại x = -1
Đúng
Sai
Câu 2 :
Cho hàm số \(f(x) = - {x^4} + 12{x^2} + 1\). a) Hàm số f(x) đồng biến trên khoảng (1;37)
Đúng
Sai
b) Số điểm cực trị của hàm số đã cho là 3
Đúng
Sai
c) Hàm số f(x) có giá trị nhỏ nhất trên đoạn [-1;2] bằng 12
Đúng
Sai
d) Hàm số f(x) có giá trị lớn nhất trên đoạn [-1;2] bằng 33
Đúng
Sai
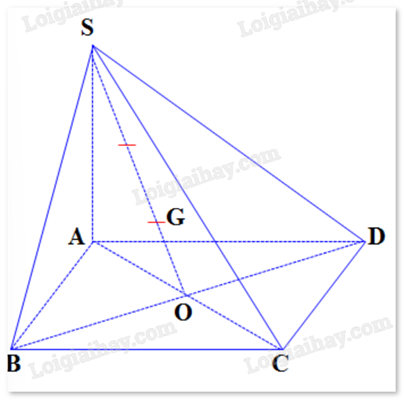
a) \(\overrightarrow {SG} = \frac{2}{3}\overrightarrow {SO} \)
Đúng
Sai
b) \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AG} \)
Đúng
Sai
c) \(\overrightarrow {SA} + \overrightarrow {SC} = 3\overrightarrow {SG} \)
Đúng
Sai
d) \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 12\overrightarrow {GO} \)
Đúng
Sai
Câu 4 :
Trong không gian Oxyz, cho vecto \(\overrightarrow a = (1;2;3)\), \(\overrightarrow b = (3;6;9)\). a) \(\overrightarrow b - \overrightarrow a = (2;4;6)\)
Đúng
Sai
b) \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương
Đúng
Sai
c) \(\left| {\overrightarrow a } \right| = \sqrt 6 \)
Đúng
Sai
d) \( - \overrightarrow b = 3\overrightarrow i + 6\overrightarrow j + 9\overrightarrow k \)
Đúng
Sai
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
Giá trị nhỏ nhất của hàm số \(f(x) = \frac{{{x^2} + 3}}{{x - 1}}\) trên đoạn [2;4] bằng bao nhiêu? Đáp án:
Câu 2 :
Tìm điều kiện của tham số m để đồ thị của hàm số \(y = \frac{{(2m + 1)x + 3}}{{x + 1}}\) có đường tiệm cận đi qua điểm A(-2;7). Đáp án:
Câu 3 :
Một cửa hàng bán một loại sản phẩm với lợi nhuận thu được khi bán x (trăm) sản phẩm được mô tả bởi hàm số \(L(x) = - 0,5{x^2} + 6x - 10\). Trong đó, x là số lượng sản phẩm bán ra, L(x) là lợi nhuận thu được (đơn vị: triệu đồng). Hãy xác định số lượng sản phẩm mà cửa hàng cần bán ra để lợi nhuận đạt mức cao nhất. Đáp án:
Câu 4 :
Cho parabol (P): \(y = {x^2}\) và điểm A(-3;0). Xác định điểm M thuộc (P) sao cho khoảng cách AM là ngắn nhất. Tung độ của điểm M bằng bao nhiêu? Đáp án:
Câu 5 :
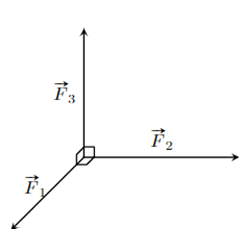
Ba lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) cùng tác động vào một vật có phương đôi một vuông góc và có độ lớn lần lượt là 2N; 3N; 4N. Hợp lực của ba lực đã cho có độ lớn bao nhiêu Niu-tơn (kết quả làm tròn đến một chữ số thập phân)?
Đáp án:
Câu 6 :
Trong không gian Oxy (đơn vị đo lấy theo km), radar phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm A(800;500;7) đến điểm B(940;550;8) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên tốc độ và hướng bay thì tọa độ của máy bay sau 10 phút tiếp theo là D(x;y;x). Khi đó, x + y + z bằng bao nhiêu? Đáp án: Lời giải và đáp án
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Cho hàm số y = f(x) xác định trên R\{-1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình. Mệnh đề nào dưới đây đúng?
Đáp án : A Phương pháp giải :
Quan sát bảng biến thiên và nhận xét. Lời giải chi tiết :
Dựa vào bảng biến thiên ta thấy trên khoảng \(( - \infty ; - 1)\) đạo hàm y' < 0 nên hàm số nghịch biến.
Câu 2 :
Hàm số \(y = \frac{{x - 2}}{{x - 1}}\) có đồ thị là hình vẽ nào sau đây? Hãy chọn câu trả lời đúng.
Đáp án : A Phương pháp giải :
Quan sát đồ thị và nhận xét. Lời giải chi tiết :
Hàm số \(y = \frac{{x - 2}}{{x - 1}}\) có tiệm cận đứng x = 1. Tiệm cận ngang y = 1 nên loại trường hợp D. Đồ thị hàm số \(y = \frac{{x - 2}}{{x - 1}}\) đi qua điểm (0; 2) nên chọn đáp án A.
Câu 3 :
Cho hàm số y = f(x) liên tục trên đoạn [–1;2] và có đồ thị như hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [–1;2]. Tính M + 2m.
Đáp án : B Phương pháp giải :
Quan sát đồ thị và nhận xét. Lời giải chi tiết :
\(M = \mathop {\max }\limits_{[ - 1;2]} f(x) = f(1) = 3\). \(M = \mathop {\min }\limits_{[ - 1;2]} f(x) = f(2) = - 2\). Vậy M + 2m = 3 + 2.(-2) = -1.
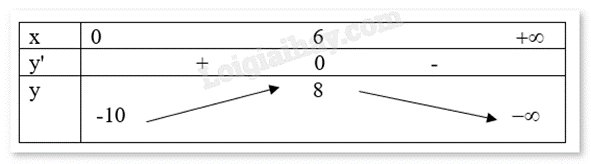
Câu 4 :
Cho hàm số y = f(x) có bảng biến thiên như sau:
Tổng số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số đã cho là:
Đáp án : C Phương pháp giải :
Quan sát bảng biến thiên và nhận xét các giới hạn. Lời giải chi tiết :
Ta có: \(\mathop {\lim }\limits_{x \to - \infty } f(x) = 2\) nên ta có tiệm cận ngang y = 2. \(\mathop {\lim }\limits_{x \to + \infty } f(x) = 5\) nên ta có tiệm cận ngang y = 5. \(\mathop {\lim }\limits_{x \to {1^ - }} f(x) = + \infty \) nên ta có tiệm cận đứng x = 1. Vậy tổng số tiệm cận đứng và tiệm cận ngang là 3.
Câu 5 :
Đường tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + 4x - 7}}{{x - 2}}\) là:
Đáp án : A Phương pháp giải :
Thực hiện phép chia đa thức (ở tử) cho đa thức (ở mẫu) ta được \(y = ax + b + \frac{M}{{cx + d}}\)(a≠0) với M là hằng số. Đường thẳng y = ax + b (a≠0) gọi là đường tiệm cận xiên của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\) \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f(x) - (ax + b)} \right] = 0\). Kết luận đường thẳng y = ax + b là đường tiệm cận xiên của đồ thị hàm số. Lời giải chi tiết :
Ta có: \(y = \frac{{{x^2} + 4x - 7}}{{x - 2}} = x + 6 + \frac{5}{{x - 2}} = f(x)\). Từ đó: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (x + 6)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{5}{{x - 2}} = 0\). Vậy đường thẳng y = x + 6 là đường tiệm cận xiên của đồ thị hàm số đã cho.
Câu 6 :
Tọa độ tâm đối xứng của đồ thị hàm số \(y = \frac{{x + 4}}{{x - 3}}\) là:
Đáp án : A Phương pháp giải :
Tìm tiệm cận ngang và tiệm cận đứng của đồ thị và tìm giao điểm của chúng. Lời giải chi tiết :
Tiệm cận ngang của đồ thị là y = 1, tiệm cận đứng của đồ thị là x = 3 nên tâm đối xứng có tọa độ (3;1).
Câu 7 :
Cho hình hộp ABCD.EFGH. Kết quả phép toán \(\overrightarrow {AB} - \overrightarrow {EH} \) là
Đáp án : D Phương pháp giải :
Dựa vào định nghĩa các vecto bằng nhau, quy tắc cộng, trừ vecto. Lời giải chi tiết :
Ta có: \(\overrightarrow {AB} = \overrightarrow {EF} \), \(\overrightarrow {DB} = \overrightarrow {HF} \) vì chúng cùng độ dài và cùng hướng. \(\overrightarrow {AB} - \overrightarrow {EH} = \overrightarrow {EF} + \overrightarrow {HE} = \overrightarrow {HF} = \overrightarrow {DB} \).
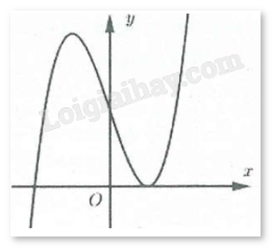
Đáp án : A Phương pháp giải :
Quan sát đồ thị và nhận xét. Lời giải chi tiết :
Dựa vào đồ thị ta thấy có hai điểm cực trị nên đây là hàm số bậc ba. Mặt khác, \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \) nên hệ số a > 0.
Câu 9 :
Giá trị lớn nhất của hàm số \(y = \sqrt {25 - {x^2}} \) trên đoạn [-4;4] là:
Đáp án : A Phương pháp giải :
Tìm đạo hàm của hàm số sau đó tính các giá trị f(x). Lời giải chi tiết :
\(f'(x) = \frac{{ - x}}{{\sqrt {25 - {x^2}} }} = 0 \Leftrightarrow x = 0\). Ta có: f(-4) = 4; f(0) = 5; f(4) = 3. Vậy giá trị lớn nhất của hàm số \(y = \sqrt {25 - {x^2}} \) trên đoạn [-4;4] bằng 5.
Câu 10 :
Cho hàm số y = f(x) có đạo hàm \(f'(x) = x(x - 2)({x^2} - 4)(x + 1)\). Hàm số y = f(x) có bao nhiêu điểm cực trị?
Đáp án : A Phương pháp giải :
Cực trị của hàm số f(x) là nghiệm bội lẻ của phương trình f’(x) = 0. Lời giải chi tiết :
Ta có: f’(x) = 0 có 3 nghiệm bội lẻ là x = 0, x = 2 và x = -1, tương ứng với 3 điểm cực trị.
Câu 11 :
Trong không gian với hệ tọa độ Oxyz, cho vecto \(\overrightarrow u = 2\overrightarrow j + 3\overrightarrow i - \overrightarrow k \). Tọa độ của vecto \(\overrightarrow u \) là
Đáp án : C Phương pháp giải :
Trong không gian có hệ trục tọa độ Oxyz, \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt là các vecto đơn vị trên các trục Ox, Oy, Oz. Lời giải chi tiết :
Tọa độ của vecto \(\overrightarrow u \) là (3;2;-1).
Câu 12 :
Cho hai vecto \(\overrightarrow u = (2; - 1;3)\), \(\overrightarrow v = ( - 3;4;1)\). Tích \(\overrightarrow u .\overrightarrow v \) bằng:
Đáp án : B Phương pháp giải :
Sử dụng công thức tính tọa độ tích vô hướng của hai vecto. Lời giải chi tiết :
Ta có: \(\overrightarrow u .\overrightarrow v = 2.( - 3) + ( - 1).4 + 3.1 = - 7\).
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
a) Hàm số f(x) đồng biến trên mỗi khoảng (0;2) và (2;3)
Đúng
Sai
b) Số điểm cực trị của hàm số đã cho là 3
Đúng
Sai
c) Hàm số f(x) có giá trị lớn nhất bằng 3
Đúng
Sai
Hàm số đạt cực tiểu tại x = -1 d) Hàm số đạt cực tiểu tại x = -1
Đúng
Sai
Đáp án
a) Hàm số f(x) đồng biến trên mỗi khoảng (0;2) và (2;3)
Đúng
Sai
b) Số điểm cực trị của hàm số đã cho là 3
Đúng
Sai
c) Hàm số f(x) có giá trị lớn nhất bằng 3
Đúng
Sai
Hàm số đạt cực tiểu tại x = -1 d) Hàm số đạt cực tiểu tại x = -1
Đúng
Sai
Phương pháp giải :
Quan sát bảng biến thiên và nhận xét. Lời giải chi tiết :
a) Sai. Hàm số f(x) nghịch biến trên (0;2). b) Đúng. Số điểm cực trị của hàm số đã cho là 3 (x = 0, x = 2, x = 3). c) Đúng. Hàm số f(x) có giá trị lớn nhất là 3. d) Sai. Hàm số đạt cực tiểu tại x = 2.
Câu 2 :
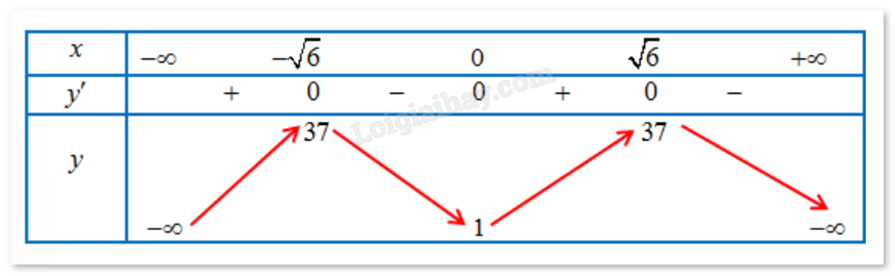
Cho hàm số \(f(x) = - {x^4} + 12{x^2} + 1\). a) Hàm số f(x) đồng biến trên khoảng (1;37)
Đúng
Sai
b) Số điểm cực trị của hàm số đã cho là 3
Đúng
Sai
c) Hàm số f(x) có giá trị nhỏ nhất trên đoạn [-1;2] bằng 12
Đúng
Sai
d) Hàm số f(x) có giá trị lớn nhất trên đoạn [-1;2] bằng 33
Đúng
Sai
Đáp án
a) Hàm số f(x) đồng biến trên khoảng (1;37)
Đúng
Sai
b) Số điểm cực trị của hàm số đã cho là 3
Đúng
Sai
c) Hàm số f(x) có giá trị nhỏ nhất trên đoạn [-1;2] bằng 12
Đúng
Sai
d) Hàm số f(x) có giá trị lớn nhất trên đoạn [-1;2] bằng 33
Đúng
Sai
Phương pháp giải :
Lập bảng biến thiên và nhận xét. Lời giải chi tiết :
\(f'(x) = - 4{x^3} + 24{x^2} = 0\) khi \(x = \sqrt 6 \), \(x = - \sqrt 6 \) hoặc x = 0. Bảng biến thiên:
Ta có: f(-1) = 12; f(2) = 33; f(0) = 1. a) Sai. Hàm số f(x) nghịch biến trên . b) Đúng. Hàm số có ba điểm cực trị (, x = 0, ). c) Sai. Hàm số f(x) có giá trị nhỏ nhất trên [-1;2] bằng 1. d) Đúng. Hàm số f(x) có giá trị lớn nhất trên [-1;2] bằng 33. a) \(\overrightarrow {SG} = \frac{2}{3}\overrightarrow {SO} \)
Đúng
Sai
b) \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AG} \)
Đúng
Sai
c) \(\overrightarrow {SA} + \overrightarrow {SC} = 3\overrightarrow {SG} \)
Đúng
Sai
d) \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 12\overrightarrow {GO} \)
Đúng
Sai
Đáp án
a) \(\overrightarrow {SG} = \frac{2}{3}\overrightarrow {SO} \)
Đúng
Sai
b) \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AG} \)
Đúng
Sai
c) \(\overrightarrow {SA} + \overrightarrow {SC} = 3\overrightarrow {SG} \)
Đúng
Sai
d) \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 12\overrightarrow {GO} \)
Đúng
Sai
Phương pháp giải :
Sử dụng quy tắc cộng vecto, lý thuyết các vecto bằng nhau, vecto đối nhau, quy tắc trọng tâm. Lời giải chi tiết :
a) Đúng. Vì hai vecto \(\overrightarrow {SG} \), \(\overrightarrow {SO} \) cùng hướng và \(\left| {\overrightarrow {SG} } \right| = \frac{2}{3}\left| {\overrightarrow {SO} } \right|\). b) Sai. Vì \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = 3\overrightarrow {AG} \) (quy tắc trọng tâm) c) Đúng. Vì \(\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} = 2.\frac{2}{3}\overrightarrow {SG} = 3\overrightarrow {SG} \). d) Đúng. Vì \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} + \overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} + 2\overrightarrow {SO} \) \( = 4\overrightarrow {SO} = 4.3\overrightarrow {GO} = 12\overrightarrow {GO} \).
Câu 4 :
Trong không gian Oxyz, cho vecto \(\overrightarrow a = (1;2;3)\), \(\overrightarrow b = (3;6;9)\). a) \(\overrightarrow b - \overrightarrow a = (2;4;6)\)
Đúng
Sai
b) \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương
Đúng
Sai
c) \(\left| {\overrightarrow a } \right| = \sqrt 6 \)
Đúng
Sai
d) \( - \overrightarrow b = 3\overrightarrow i + 6\overrightarrow j + 9\overrightarrow k \)
Đúng
Sai
Đáp án
a) \(\overrightarrow b - \overrightarrow a = (2;4;6)\)
Đúng
Sai
b) \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương
Đúng
Sai
c) \(\left| {\overrightarrow a } \right| = \sqrt 6 \)
Đúng
Sai
d) \( - \overrightarrow b = 3\overrightarrow i + 6\overrightarrow j + 9\overrightarrow k \)
Đúng
Sai
Phương pháp giải :
Sử dụng các quy tắc cộng, trừ vecto, nhân vecto với một số, khái niệm hai vecto cùng phương, công thức tính độ dài vecto. Lời giải chi tiết :
a) Đúng. Vì \(\overrightarrow b - \overrightarrow a = (3 - 1;6 - 2;9 - 3) = (2;4;6)\). b) Đúng. Vì \(\frac{1}{3} = \frac{2}{6} = \frac{3}{9}\) nên \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương. c) Sai. Vì \(\left| {\overrightarrow a } \right| = \sqrt {{1^2} + {2^2} + {3^2}} = \sqrt {14} \). d) Sai. Vì \( - \overrightarrow b = ( - 3; - 6; - 9) = - 3\overrightarrow i - 6\overrightarrow j - 9\overrightarrow k \).
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
Giá trị nhỏ nhất của hàm số \(f(x) = \frac{{{x^2} + 3}}{{x - 1}}\) trên đoạn [2;4] bằng bao nhiêu? Đáp án: Đáp án
Đáp án: Phương pháp giải :
- Tính y’, tìm các nghiệm của y’ = 0 - Tìm giá trị y tại các điểm cực trị của hàm số và hai đầu mút của đoạn. Lời giải chi tiết :
Ta có: \(f'(x) = \frac{{{x^2} - 2x - 3}}{{{{(x - 1)}^2}}} = 0\) khi x = -1 hoặc x = 3. Xét đoạn [2;4] có: f(2) = 7; f(3) = 6; \(f(4) = \frac{{19}}{3}\). Vậy giá trị nhỏ nhất của hàm số trên [2;4] là 6.
Câu 2 :
Tìm điều kiện của tham số m để đồ thị của hàm số \(y = \frac{{(2m + 1)x + 3}}{{x + 1}}\) có đường tiệm cận đi qua điểm A(-2;7). Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng quy tắc tìm đường tiệm cận của hàm phân thức. Lời giải chi tiết :
Nếu m = 1, ta có hàm số \(y = \frac{{3x + 3}}{{x + 1}} = 3\) không có tiệm cận qua A(-2;7). Nếu \(m \ne 1\), đồ thị có tiệm cận đứng x = -1 và tiệm cận ngang y = 2m + 1. Như vậy, để thỏa mãn yêu cầu đề bài, tiệm cận ngang phải đi qua A, khi và chỉ khi 2m + 1 = 7, tức m = 3.
Câu 3 :
Một cửa hàng bán một loại sản phẩm với lợi nhuận thu được khi bán x (trăm) sản phẩm được mô tả bởi hàm số \(L(x) = - 0,5{x^2} + 6x - 10\). Trong đó, x là số lượng sản phẩm bán ra, L(x) là lợi nhuận thu được (đơn vị: triệu đồng). Hãy xác định số lượng sản phẩm mà cửa hàng cần bán ra để lợi nhuận đạt mức cao nhất. Đáp án: Đáp án
Đáp án: Phương pháp giải :
Tìm x để hàm số \(L(x) = - 0,5{x^2} + 6x - 10\) đạt giá trị lớn nhất. Lời giải chi tiết :
Lợi nhuận đạt mức cao nhất khi \(L(x) = - 0,5{x^2} + 6x - 10\) đạt giá trị lớn nhất. Ta có: \(L'(x) = - x + 6 = 0 \Leftrightarrow x = 6\).
Theo bảng biến thiên, L(x) đạt giá trị lớn nhất khi x = 6 (trăm). Vậy lợi nhuận đạt mức cao nhất khi bán ra 600 sản phẩm.
Câu 4 :
Cho parabol (P): \(y = {x^2}\) và điểm A(-3;0). Xác định điểm M thuộc (P) sao cho khoảng cách AM là ngắn nhất. Tung độ của điểm M bằng bao nhiêu? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Thiết lập hàm số biểu diễn bình phương độ dài AM theo biến x là hoành độ. Lập bảng biến thiên cho hàm số, tìm x để hàm số đó đạt giá trị nhỏ nhất. Lời giải chi tiết :
Gọi \(M(x;{x^2})\) là một điểm bất kì của parabol (P). Ta có: \(A{M^2} = {(x + 3)^2} + {x^4} = {x^4} + {x^2} + 6x + 9\). AM nhỏ nhất khi và chỉ khi \(f(x) = A{M^2}\) nhỏ nhất. Xét \(f(x) = {x^4} + {x^2} + 6x + 9\). Có \(f'(x) = 4{x^3} + 2x + 6 = 0 \Leftrightarrow x = - 1\).
Dựa vào bảng biến thiên, ta suy ra f(x) đạt giá trị nhỏ nhất tại x = -1. Như vậy, điểm M cần tìm có tọa độ (-1;1). Tung độ của M bằng 1.
Câu 5 :
Ba lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) cùng tác động vào một vật có phương đôi một vuông góc và có độ lớn lần lượt là 2N; 3N; 4N. Hợp lực của ba lực đã cho có độ lớn bao nhiêu Niu-tơn (kết quả làm tròn đến một chữ số thập phân)?
Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng quy tắc hình hộp. Lời giải chi tiết :
Vì ba vecto trên đôi một vuông góc nên ta có thể áp dụng quy tắc hình hộp. Hợp lực F của ba vecto trên có độ lớn là: \(F = \sqrt {F_1^2 + F_2^2 + F_3^2} = \sqrt {{2^2} + {3^2} + {4^2}} = \sqrt {29} \approx 5,4\) (N).
Câu 6 :
Trong không gian Oxy (đơn vị đo lấy theo km), radar phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm A(800;500;7) đến điểm B(940;550;8) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên tốc độ và hướng bay thì tọa độ của máy bay sau 10 phút tiếp theo là D(x;y;x). Khi đó, x + y + z bằng bao nhiêu? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng quy tắc cộng vecto. Lời giải chi tiết :
Máy bay di chuyển với tốc độ không đổi, sau 10 phút sẽ đi được quãng đường đúng bằng quãng đường 10 phút trước, tức AB = BD. Mặt khác, hướng bay giữ nguyên nên \(\overrightarrow {AB} = \overrightarrow {BD} = (940 - 800;550 - 500;8 - 7) = (140;50;1)\). Ta tính được \(D = (940 + 140;550 + 50;8 + 1) = (1080;600;9)\). Vậy x + y + z = 1689.
|






















Danh sách bình luận