Đề thi, đề kiểm tra Toán lớp 10 - Cánh diều

Đề thi giữa kì 1 Toán 10 Cánh diều - Đề số 11

Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Cánh diều

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

Tải về

Tải về đề thi và đáp án Tải về đề thi Tải về đáp án
Làm đề thi

Phần trắc nghiệm

Đề bài

Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :

Cho mệnh đề A: “32 là số tự nhiên chẵn”. Mệnh đề phủ định của mệnh đề A là

  • A

    32 là số chẵn

  • B

    32 là số tự nhiên

  • C

    32 không là số tự nhiên chẵn

  • D

    32 là số nguyên tố

Câu 2 :

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

  • A

    \({x^2} + 4y > 0\)

  • B

    \({x^2} + {y^2} < 3\)

  • C

    \(x + 5{y^2} \ge 0\)

  • D

    \(x + 2y \ge 0\)

Câu 3 :

Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + 3y - 2 \ge 0}\\{2x + y + 1 \le 0}\end{array}} \right.\). Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình đã cho?

  • A

    M(0;1)

  • B

    N(-1;1)

  • C

    P(1;3)

  • D

    Q(-1;0)

Câu 4 :

Trong mặt phẳng Oxy, điểm nào trong các điểm sau không thuộc miền nghiệm của bất phương trình x – 4y + 5 > 0?

  • A

    (2;1)

  • B

    (-5;0)

  • C

    (0;0)

  • D

    (1;-3)

Câu 5 :

Trong tam giác ABC với BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp tam giác ABC. Hệ thức nào sau đây đúng?

  • A

    \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = R\)

  • B

    \(\frac{a}{{\cos A}} = \frac{b}{{\cos B}} = \frac{c}{{\cos C}} = R\)

  • C

    \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)

  • D

    \(\frac{a}{{\cos A}} = \frac{b}{{\cos B}} = \frac{c}{{\cos C}} = 2R\)

Câu 6 :

Cho các tập hợp A = (-5;3) và B = [-2;7). Tìm \(A \cup B\).

  • A

    [-2;3)

  • B

    (-5;-2)

  • C

    (-5;7)

  • D

    [3;7)

Câu 7 :

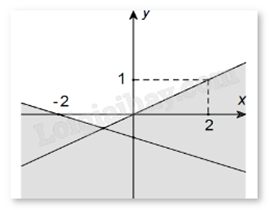
Phần không tô đậm (không kể biên) trong hình vẽ sau biểu diễn miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình cho dưới đây?

  • A

    \(\left\{ {\begin{array}{*{20}{c}}{x - 2y \le 0}\\{x + 3y \ge  - 2}\end{array}} \right.\)

  • B

    \(\left\{ {\begin{array}{*{20}{c}}{x - 2y > 0}\\{x + 3y <  - 2}\end{array}} \right.\)

  • C

    \(\left\{ {\begin{array}{*{20}{c}}{x - 2y \le 0}\\{x + 3y \le  - 2}\end{array}} \right.\)

  • D

    \(\left\{ {\begin{array}{*{20}{c}}{x - 2y < 0}\\{x + 3y >  - 2}\end{array}} \right.\)

Câu 8 :

Trong các đẳng thức sau, đẳng thức nào đúng?

  • A

    \(\sin ({180^o} - \alpha ) =  - \cos \alpha \)

  • B

    \(\sin ({180^o} - \alpha ) =  - \sin \alpha \)

  • C

    \(\sin ({180^o} - \alpha ) = \cos \alpha \)

  • D

    \(\sin ({180^o} - \alpha ) = \sin \alpha \)

Câu 9 :

Với \(x \in \mathbb{R}\), tìm mệnh đề đúng trong các mệnh đề sau.

  • A

    \(\forall x \in [ - 3;2) \Leftrightarrow  - 3 < x < 2\)

  • B

    \(\forall x \in [ - 3;2) \Leftrightarrow  - 3 \le x \le 2\)

  • C

    \(\forall x \in [ - 3;2) \Leftrightarrow  - 3 \le x < 2\)

  • D

    \(\forall x \in [ - 3;2) \Leftrightarrow  - 3 < x \le 2\)

Câu 10 :

Tam giác ABC có AB = 4 cm, AC = 8 cm, \(\widehat {BAC} = {60^o}\). Tính diện tích tam giác ABC.

  • A

    \({S_{\Delta ABC}} = 8\sqrt 3 \)

  • B

    \({S_{\Delta ABC}} = 4\sqrt 3 \)

  • C

    \({S_{\Delta ABC}} = 16\sqrt 3 \)

  • D

    \({S_{\Delta ABC}} = 8\)

Câu 11 :

Cho mệnh đề chứa biến P(x): \(x + 2 > {x^2}\). Mệnh đề nào sau đây đúng?

  • A

    P(3)

  • B

    P(-1)

  • C

    P(1)

  • D

    P(5)

Câu 12 :

Cho tam giác MNP vuông tại M, NP = 16 và \(\widehat {PNM} = {30^o}\). Tính độ dài cạnh MP.

  • A

    \(8\sqrt 3 \)

  • B

    8

  • C

    32

  • D

    16

Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :

Cho \(P(n) = {n^2} - 6n + 10\) với n là số tự nhiên.

P(1) chia hết cho 3.

Đúng
Sai

P(2) là số chẵn.

Đúng
Sai

P(2n) > P(n) – 1 với n = 1.

Đúng
Sai

Tồn tại số tự nhiên n thỏa mãn điều kiện \(\frac{{2P(n) - 1}}{{n - 3}}\) là số nguyên.

Đúng
Sai
Câu 2 :

Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo.

Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu.

Để pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu.

Gọi x, y lần lượt là số lít nước cam, nước táo được tạo thành.

a) Biểu thức biểu diễn số gam đường cần dùng là 30x + 10y.

Đúng
Sai

b) Biểu thức biểu diễn số gam hương liệu cần dùng là x + y.

Đúng
Sai

Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 21}\\{x + y \le 9}\\{x + 4y \le 24}\end{array}} \right.\).

Đúng
Sai

d) Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Để điểm thưởng lớn nhất thì cần pha chế 4 lít nước cam và 5 lít nước táo.

Đúng
Sai
Câu 3 :

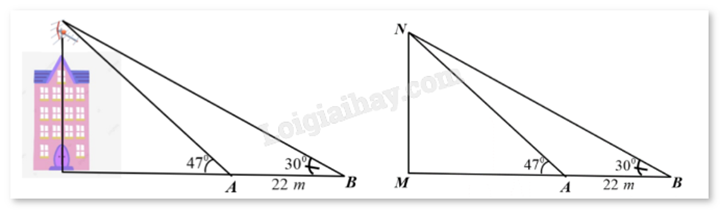
Trên một nóc nhà có một cột ăng-ten cao 5m. Từ hai vị trí quan sát A và B cách nhau 22m, người ta có thể nhìn thấy đỉnh của cột ăng-ten một góc \({47^o}\) và \({30^o}\) so với phương nằm ngang (như hình vẽ). Khi đó

a) \(\widehat {MNA} = {43^o}\).

Đúng
Sai

b) \(\widehat {ANB} = {60^o}\).

Đúng
Sai

c) Khoảng cách từ đỉnh cột ăng-ten đến vị trí B không quá 56m.

Đúng
Sai

d) Chiều cao của ngôi nhà là 25m.

Đúng
Sai
Câu 4 :

Cho các tập hợp \(A = \{ x \in \mathbb{N}|x \le 5\} \), \(B = \{ x \in \mathbb{Z}|{x^2} + x - 2 = 0\} \) và \(C = \{  - 2; - 1;1;4\} \).

a) \(A \cap B = \{  - 2;1\} \).

Đúng
Sai

b) \(A \cup B = \{  - 2;0;1;2;3;4;5\} \).

Đúng
Sai

c) \(B \subset C\).

Đúng
Sai

d) \({C_\mathbb{N}}A = (5; + \infty )\).

Đúng
Sai
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :

Với giá trị nào của x thì “\(x \in \mathbb{N},{x^2} - 4 = 0\)” là mệnh đề đúng?

Đáp án:

Câu 2 :

Cho tam giác ABC có cạnh AC = 14, \(\widehat B = {120^o}\), tổng hai cạnh còn lại là 16. Tính độ dài cạnh BC biết BC > AB.

Đáp án:

Câu 3 :

Cho \(\alpha \) là góc tù và \(\tan \alpha  + \cot \alpha  =  - 2\). Tính giá trị biểu thức \(M = \frac{{\sqrt 2 }}{4}(\sin \alpha  - \cos \alpha )\) (viết kết quả dưới dạng số thập phân).

Đáp án:

Câu 4 :

Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 100 kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 5 triệu đồng, có thể chiết xuất được 20 kg chất A. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng có thể chiết xuất được 1,5 kg chất B. Biết mỗi kg chất A có giá 0,5 triệu đồng, mỗi kg chất B có giá 5 triệu đồng. Hỏi phải dùng bao nhiêu tấn nguyên liệu loại I để lợi nhuận thu về là lớn nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 8 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II.

Đáp án:

Câu 5 :

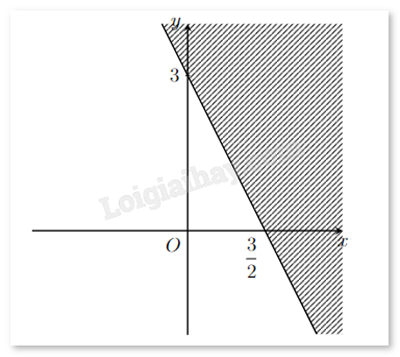
Biểu diễn hình học miền nghiệm (không tô màu) của bất phương trình \(ax + by \le c\) như hình vẽ. Biết rằng \(a,b \in \mathbb{N}*\). Tính a + b.

Đáp án:

Câu 6 :

Một nhóm có 12 học sinh chuẩn bị cho hội diễn văn nghệ. Trong danh sách đăng kí tham gia tiết mục múa và tiết mục hát của nhóm đó, có 5 học sinh tham gia tiết mục múa, 3 học sinh tham gia cả hai tiết mục. Hỏi có bao nhiêu học sinh trong nhóm tham gia tiết mục hát? Biết có 4 học sinh của nhóm không tham gia tiết mục nào.

Đáp án:

Lời giải và đáp án

Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :

Cho mệnh đề A: “32 là số tự nhiên chẵn”. Mệnh đề phủ định của mệnh đề A là

  • A

    32 là số chẵn

  • B

    32 là số tự nhiên

  • C

    32 không là số tự nhiên chẵn

  • D

    32 là số nguyên tố

Đáp án : C

Phương pháp giải :

Cho mệnh đề P. Mệnh đề “Không phải P” được gọi là mệnh đề phủ định của mệnh đề P.

Lời giải chi tiết :

Mệnh đề phủ định của mệnh đề A là “32 không là số tự nhiên chẵn”.

Câu 2 :

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

  • A

    \({x^2} + 4y > 0\)

  • B

    \({x^2} + {y^2} < 3\)

  • C

    \(x + 5{y^2} \ge 0\)

  • D

    \(x + 2y \ge 0\)

Đáp án : D

Phương pháp giải :

Dựa vào định nghĩa bất phương trình bậc nhất hai ẩn.

Lời giải chi tiết :

Các bất phương trình ở đáp án A, B, C đều là bất phương trình bậc hai. Chỉ có bất phương trình ở đáp án D là bất phương trình bậc nhất hai ẩn.

Câu 3 :

Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + 3y - 2 \ge 0}\\{2x + y + 1 \le 0}\end{array}} \right.\). Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình đã cho?

  • A

    M(0;1)

  • B

    N(-1;1)

  • C

    P(1;3)

  • D

    Q(-1;0)

Đáp án : B

Phương pháp giải :

Thay lần lượt tọa độ của các điểm đã cho vào hai bất phương trình có trong hệ, nếu thỏa mãn hai bất phương trình trong hệ thì điểm đó thuộc miền nghiệm của hệ bất phương trình.

Lời giải chi tiết :

Với M(0;1) ta có \(\left\{ {\begin{array}{*{20}{c}}{0 + 3.1 - 2 \ge 0}\\{2.0 + 1 + 1 \le 0}\end{array}} \right.\). Thấy bất phương trình thứ 2 của hệ sai. Vậy A sai.

Với N(-1;1) ta có \(\left\{ {\begin{array}{*{20}{c}}{ - 1 + 3.1 - 2 \ge 0}\\{2.( - 1) + 1 + 1 \le 0}\end{array}} \right.\). Thấy cả hai bất phương trình của hệ đúng. Vậy b đúng.

Với P(1;3) ta có \(\left\{ {\begin{array}{*{20}{c}}{1 + 3.3 - 2 \ge 0}\\{2.1 + 3 + 1 \le 0}\end{array}} \right.\). Thấy bất phương trình thứ 2 của hệ sai. Vậy C sai.

Với Q(-1;0) ta có \(\left\{ {\begin{array}{*{20}{c}}{ - 1 + 3.0 - 2 \ge 0}\\{2.( - 1) + 0 + 1 \le 0}\end{array}} \right.\). Thấy bất phương trình thứ 1 của hệ sai. Vậy D sai.

Câu 4 :

Trong mặt phẳng Oxy, điểm nào trong các điểm sau không thuộc miền nghiệm của bất phương trình x – 4y + 5 > 0?

  • A

    (2;1)

  • B

    (-5;0)

  • C

    (0;0)

  • D

    (1;-3)

Đáp án : B

Phương pháp giải :

Thay lần lượt tọa độ các điểm đã cho vào bất phương trình x – 4y + 5 > 0, nếu thỏa mãn thì điểm đó thuộc miền nghiệm của bất phương trình đã cho.

Lời giải chi tiết :

Với điểm có tọa độ (2;1) ta thấy bất phương trình 2 – 4.1 + 5 > 0 đúng.

Với điểm có tọa độ (-5;0) ta thấy bất phương trình -5 – 4.0 + 5 > 0 sai.

Với điểm có tọa độ (0;0) ta thấy bất phương trình 0 – 4.0 + 5 > 0 đúng.

Với điểm có tọa độ (1;-3) ta thấy bất phương trình 1 – 4.(-3) + 5 > 0 đúng.

Câu 5 :

Trong tam giác ABC với BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp tam giác ABC. Hệ thức nào sau đây đúng?

  • A

    \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = R\)

  • B

    \(\frac{a}{{\cos A}} = \frac{b}{{\cos B}} = \frac{c}{{\cos C}} = R\)

  • C

    \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)

  • D

    \(\frac{a}{{\cos A}} = \frac{b}{{\cos B}} = \frac{c}{{\cos C}} = 2R\)

Đáp án : C

Phương pháp giải :

Dựa vào định lí Sin trong tam giác.

Lời giải chi tiết :

Trong tam giác ABC với BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp tam giác ABC, ta có \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\).

Câu 6 :

Cho các tập hợp A = (-5;3) và B = [-2;7). Tìm \(A \cup B\).

  • A

    [-2;3)

  • B

    (-5;-2)

  • C

    (-5;7)

  • D

    [3;7)

Đáp án : C

Phương pháp giải :

Hợp của hai tập hợp A và B là tập hợp gồm các phần tử thuộc tập hợp A hoặc thuộc tập hợp B.

Lời giải chi tiết :

\(A \cup B = ( - 5;7)\).

Câu 7 :

Phần không tô đậm (không kể biên) trong hình vẽ sau biểu diễn miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình cho dưới đây?

  • A

    \(\left\{ {\begin{array}{*{20}{c}}{x - 2y \le 0}\\{x + 3y \ge  - 2}\end{array}} \right.\)

  • B

    \(\left\{ {\begin{array}{*{20}{c}}{x - 2y > 0}\\{x + 3y <  - 2}\end{array}} \right.\)

  • C

    \(\left\{ {\begin{array}{*{20}{c}}{x - 2y \le 0}\\{x + 3y \le  - 2}\end{array}} \right.\)

  • D

    \(\left\{ {\begin{array}{*{20}{c}}{x - 2y < 0}\\{x + 3y >  - 2}\end{array}} \right.\)

Đáp án : D

Phương pháp giải :

Xét miền nghiệm có chứa biên hay không.

Thay tọa độ của điểm bất kì vào hệ phương trình xem có thỏa mãn không.

Dùng phương pháp loại trừ.

Lời giải chi tiết :

Do miền nghiệm không chứa biên nên ta loại đáp án A và C.

Lấy điểm M(0;1) thuộc miền nghiệm của hệ bất phương trình, thay tọa độ điểm M vào đáp án B, D.

Xét đáp án B, ta thấy \(\left\{ {\begin{array}{*{20}{c}}{0 - 2.1 > 0}\\{0 + 3.1 <  - 2}\end{array}} \right.\) không thỏa mãn. Loại B.

 Xét đáp án D, ta thấy \(\left\{ {\begin{array}{*{20}{c}}{0 - 2.1 < 0}\\{0 + 3.1 >  - 2}\end{array}} \right.\) thỏa mãn. Chọn D.

Câu 8 :

Trong các đẳng thức sau, đẳng thức nào đúng?

  • A

    \(\sin ({180^o} - \alpha ) =  - \cos \alpha \)

  • B

    \(\sin ({180^o} - \alpha ) =  - \sin \alpha \)

  • C

    \(\sin ({180^o} - \alpha ) = \cos \alpha \)

  • D

    \(\sin ({180^o} - \alpha ) = \sin \alpha \)

Đáp án : D

Phương pháp giải :

Dựa vào mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau.

Lời giải chi tiết :

Với hai góc bù nhau \(\alpha \) và \({180^o} - \alpha \), ta có \(\sin ({180^o} - \alpha ) = \sin \alpha \).

Câu 9 :

Với \(x \in \mathbb{R}\), tìm mệnh đề đúng trong các mệnh đề sau.

  • A

    \(\forall x \in [ - 3;2) \Leftrightarrow  - 3 < x < 2\)

  • B

    \(\forall x \in [ - 3;2) \Leftrightarrow  - 3 \le x \le 2\)

  • C

    \(\forall x \in [ - 3;2) \Leftrightarrow  - 3 \le x < 2\)

  • D

    \(\forall x \in [ - 3;2) \Leftrightarrow  - 3 < x \le 2\)

Đáp án : C

Phương pháp giải :

\(\forall x \in [a;b) \Leftrightarrow a \le x < b\).

Lời giải chi tiết :

Với \(x \in \mathbb{R}\) thì \(\forall x \in [ - 3;2) \Leftrightarrow  - 3 \le x < 2\).

Câu 10 :

Tam giác ABC có AB = 4 cm, AC = 8 cm, \(\widehat {BAC} = {60^o}\). Tính diện tích tam giác ABC.

  • A

    \({S_{\Delta ABC}} = 8\sqrt 3 \)

  • B

    \({S_{\Delta ABC}} = 4\sqrt 3 \)

  • C

    \({S_{\Delta ABC}} = 16\sqrt 3 \)

  • D

    \({S_{\Delta ABC}} = 8\)

Đáp án : A

Phương pháp giải :

Áp dụng công thức \({S_{\Delta ABC}} = \frac{1}{2}AB.AC.\sin \widehat {BAC}\).

Lời giải chi tiết :

Ta có \({S_{\Delta ABC}} = \frac{1}{2}AB.AC.\sin \widehat {BAC} = \frac{1}{2}4.8\sin {60^o} = 8\sqrt 3 \).

Câu 11 :

Cho mệnh đề chứa biến P(x): \(x + 2 > {x^2}\). Mệnh đề nào sau đây đúng?

  • A

    P(3)

  • B

    P(-1)

  • C

    P(1)

  • D

    P(5)

Đáp án : C

Phương pháp giải :

Xét từng mệnh đề.

Lời giải chi tiết :

Ta có:

P(3): \(3 + 2 > {3^2}\) là mệnh đề sai. Loại A.

P(-1): \( - 1 + 2 > {( - 1)^2}\) là mệnh đề sai. Loại B.

P(1): \(1 + 2 > {1^2}\) là mệnh đề đúng. Chọn C.

P(3): \(5 + 2 > {5^2}\) là mệnh đề sai. Loại D.

Câu 12 :

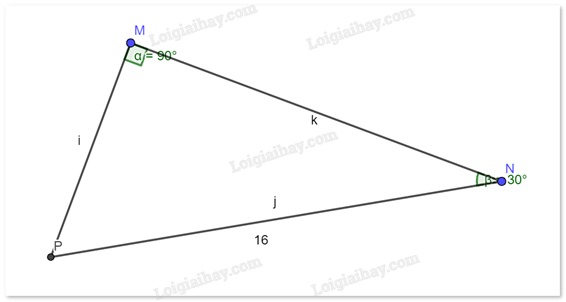
Cho tam giác MNP vuông tại M, NP = 16 và \(\widehat {PNM} = {30^o}\). Tính độ dài cạnh MP.

  • A

    \(8\sqrt 3 \)

  • B

    8

  • C

    32

  • D

    16

Đáp án : B

Phương pháp giải :

Sử dụng hệ thức lượng trong tam giác vuông.

Lời giải chi tiết :

Xét tam giác MNP vuông tại M có \(\sin \widehat {MNP} = \frac{{MP}}{{NP}}\), suy ra \(MP = NP\sin \widehat {MNP} = 16\sin {30^o} = 8\).

Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :

Cho \(P(n) = {n^2} - 6n + 10\) với n là số tự nhiên.

P(1) chia hết cho 3.

Đúng
Sai

P(2) là số chẵn.

Đúng
Sai

P(2n) > P(n) – 1 với n = 1.

Đúng
Sai

Tồn tại số tự nhiên n thỏa mãn điều kiện \(\frac{{2P(n) - 1}}{{n - 3}}\) là số nguyên.

Đúng
Sai
Đáp án

P(1) chia hết cho 3.

Đúng
Sai

P(2) là số chẵn.

Đúng
Sai

P(2n) > P(n) – 1 với n = 1.

Đúng
Sai

Tồn tại số tự nhiên n thỏa mãn điều kiện \(\frac{{2P(n) - 1}}{{n - 3}}\) là số nguyên.

Đúng
Sai
Phương pháp giải :

a) Tính P(1) bằng cách thay n = 1 vào biểu thức P(n) rồi nhận xét.

b) Tính P(2) bằng cách thay n = 2 vào biểu thức P(n) rồi nhận xét.

c) Tính P(2n) và P(n) – 1 bằng cách thay n = 1 vào biểu thức P(n) rồi nhận xét.

d) Viết lại đa thức \(\frac{{2P(n) - 1}}{{n - 3}}\) dưới dạng \(an + b + \frac{c}{{n - 3}}\) rồi tìm n sao cho n – 3 là ước của c.

Lời giải chi tiết :

a) Sai. \(P(1) = {1^2} - 6.1 + 10 = 5\). Vậy P(1) không chia hết cho 3.

b) Đúng. \(P(2) = {2^2} - 6.2 + 10 = 2\). Vậy P(2) là số chẵn.

c) Sai. \(P(2n) = P(2) = 2\), \(P(n) - 1 = P(1) - 1 = 5 - 1 = 4\). Vậy P(2n) < P(n).

d) Sai. \(\frac{{2P(n) - 1}}{{n - 3}} = \frac{{{n^2} - 12n + 19}}{{n - 3}} = 2n - 6 + \frac{1}{{n - 3}}\) là số nguyên khi và chỉ khi n – 3 là ước của 1.

Vì không tồn tại số tự nhiên n thỏa mãn nên mệnh đề sai.

Câu 2 :

Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo.

Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu.

Để pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu.

Gọi x, y lần lượt là số lít nước cam, nước táo được tạo thành.

a) Biểu thức biểu diễn số gam đường cần dùng là 30x + 10y.

Đúng
Sai

b) Biểu thức biểu diễn số gam hương liệu cần dùng là x + y.

Đúng
Sai

Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 21}\\{x + y \le 9}\\{x + 4y \le 24}\end{array}} \right.\).

Đúng
Sai

d) Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Để điểm thưởng lớn nhất thì cần pha chế 4 lít nước cam và 5 lít nước táo.

Đúng
Sai
Đáp án

a) Biểu thức biểu diễn số gam đường cần dùng là 30x + 10y.

Đúng
Sai

b) Biểu thức biểu diễn số gam hương liệu cần dùng là x + y.

Đúng
Sai

Cặp (x; y) thỏa mãn bài toán thuộc miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 21}\\{x + y \le 9}\\{x + 4y \le 24}\end{array}} \right.\).

Đúng
Sai

d) Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Để điểm thưởng lớn nhất thì cần pha chế 4 lít nước cam và 5 lít nước táo.

Đúng
Sai
Phương pháp giải :

Lập hệ bất phương trình.

Lời giải chi tiết :

a) Đúng. Biểu thức biểu diễn số gam đường cần dùng là 30x + 10y.

b) Sai. Biểu thức biểu diễn số gam hương liệu cần dùng là x + 4y.

c) Đúng. Với x, y lần lượt là số lít nước cam, nước táo được tạo thành, ta có:

30x + 10y là số gam đường cần dùng.

x + y là số lít nước cần dùng.

x + 4y là số gam hương liệu cần dùng.

Theo giả thiết ta có  \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{30x + 10y \le 210}\\{x + y \le 9}\\{x + 4y \le 24}\end{array}} \right.\) hay \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{3x + y \le 21}\\{x + y \le 9}\\{x + 4y \le 24}\end{array}} \right.\).

d) Đúng. Vẽ miền nghiệm của hệ:

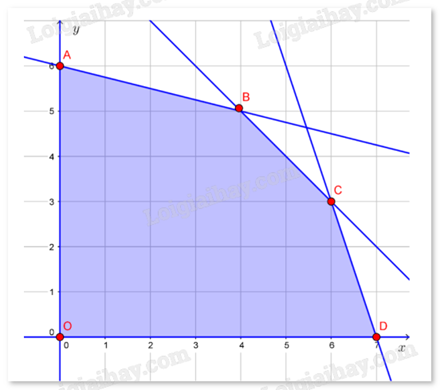
Ta thấy miền nghiệm của hệ là một miền ngũ giác OABCD kể cả biên, trong đó O(0;0), A(0;6), B(4;5), C(6;3) và D(7;0).

Số điểm thưởng nhận được là P = 60x + 80y.

P đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác. Thay tọa độ các điểm trên vào P, thấy P đạt giá trị lớn nhất bằng 640 tại B(4;5).

Vậy, cần pha chế 4 lít nước cam và 5 lít nước táo.

Câu 3 :

Trên một nóc nhà có một cột ăng-ten cao 5m. Từ hai vị trí quan sát A và B cách nhau 22m, người ta có thể nhìn thấy đỉnh của cột ăng-ten một góc \({47^o}\) và \({30^o}\) so với phương nằm ngang (như hình vẽ). Khi đó

a) \(\widehat {MNA} = {43^o}\).

Đúng
Sai

b) \(\widehat {ANB} = {60^o}\).

Đúng
Sai

c) Khoảng cách từ đỉnh cột ăng-ten đến vị trí B không quá 56m.

Đúng
Sai

d) Chiều cao của ngôi nhà là 25m.

Đúng
Sai
Đáp án

a) \(\widehat {MNA} = {43^o}\).

Đúng
Sai

b) \(\widehat {ANB} = {60^o}\).

Đúng
Sai

c) Khoảng cách từ đỉnh cột ăng-ten đến vị trí B không quá 56m.

Đúng
Sai

d) Chiều cao của ngôi nhà là 25m.

Đúng
Sai
Phương pháp giải :

a) Sử dụng tính chất của hai góc phụ nhau trong tam giác vuông.

b) Cộng trừ số đo hai góc kề nhau.

c) Sử dụng định lí Sin trong tam giác.

d) Sử dụng hệ thức lượng trong tam giác vuông.

Lời giải chi tiết :

a) Đúng. Xét tam giác AMN vuông tại M có \(\widehat {MNA} = {90^o} - \widehat {MAN} = {90^o} - {47^o} = {43^o}\).

b) Sai. Xét tam giác BMN vuông tại M có \(\widehat {MNB} = {90^o} - \widehat {MBN} = {90^o} - {30^o} = {60^o}\).

Ta có \(\widehat {ANB} = \widehat {BNM} - \widehat {ANM} = {60^o} - {43^o} = {17^o}\).

c) Đúng. Ta có \(\widehat {NAB} = {180^o} - \widehat {MAN} = {180^o} - {47^o} = {133^o}\).

Xét tam giác NAB có \(\frac{{NB}}{{\sin \widehat {NAB}}} = \frac{{AB}}{{\sin \widehat {ANB}}}\), suy ra \(NB = \frac{{22\sin {{133}^o}}}{{\sin {{17}^o}}} \approx 55\) (m).

d) Sai. Xét tam giác BMN vuông tại M có \(\sin \widehat {MBN} = \frac{{MN}}{{AB}}\), suy ra \(MN = NB\sin \widehat {MBN} = 55\sin {30^o} = 27,5\).

Chiều cao của ngôi nhà là 27,5 – 5 = 22,5 (m).

Câu 4 :

Cho các tập hợp \(A = \{ x \in \mathbb{N}|x \le 5\} \), \(B = \{ x \in \mathbb{Z}|{x^2} + x - 2 = 0\} \) và \(C = \{  - 2; - 1;1;4\} \).

a) \(A \cap B = \{  - 2;1\} \).

Đúng
Sai

b) \(A \cup B = \{  - 2;0;1;2;3;4;5\} \).

Đúng
Sai

c) \(B \subset C\).

Đúng
Sai

d) \({C_\mathbb{N}}A = (5; + \infty )\).

Đúng
Sai
Đáp án

a) \(A \cap B = \{  - 2;1\} \).

Đúng
Sai

b) \(A \cup B = \{  - 2;0;1;2;3;4;5\} \).

Đúng
Sai

c) \(B \subset C\).

Đúng
Sai

d) \({C_\mathbb{N}}A = (5; + \infty )\).

Đúng
Sai
Phương pháp giải :

a) Giao của hai tập hợp là tập hợp gồm các phần tử thuộc cả hai tập hợp.

b) Hợp của hai tập hợp là tập hợp gồm các phần tử thuộc một trong hai tập hợp hoặc thuộc cả hai tập hợp.

c) Tập hợp con của tập hợp A có các phần tử đều thuộc tập hợp A (kể cả tập hợp rỗng và A).

d) \({C_\mathbb{N}}A\) là phần bù của A trong \(\mathbb{N}\).

Lời giải chi tiết :

Ta có: \(A = \{ 0;1;2;3;4;5\} \), \(B = \{  - 2;1\} \), \(C = \{  - 2; - 1;1;4\} \).

a) Sai. \(A \cap B = \{ 1\} \).

b) Đúng. \(A \cup B = \{  - 2;0;1;2;3;4;5\} \).

c) Đúng. \(B \subset C\).

d) Đúng. \({C_\mathbb{N}}A = \mathbb{N}\backslash A = (5; + \infty )\).

Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :

Với giá trị nào của x thì “\(x \in \mathbb{N},{x^2} - 4 = 0\)” là mệnh đề đúng?

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Mệnh đề đúng khi giá trị của x là nghiệm của phương trình \({x^2} - 4 = 0\) và \(x \in \mathbb{N}\).

Lời giải chi tiết :

Ta có: \({x^2} - 4 = 0\)

Suy ra \(x =  \pm 2\).

Mà \(x \in \mathbb{N}\) nên \(x = 2\).

Câu 2 :

Cho tam giác ABC có cạnh AC = 14, \(\widehat B = {120^o}\), tổng hai cạnh còn lại là 16. Tính độ dài cạnh BC biết BC > AB.

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Sử dụng định lí Cosin trong tam giác.

Lời giải chi tiết :

Áp dụng định lí Cosin trong tam giác ABC có:

\(A{C^2} = B{C^2} + A{B^2} - 2BC.AB\cos B\)

\({14^2} = B{C^2} + A{B^2} - 2BC.AB.\cos {120^o}\)

\( 196 = B{C^2} + A{B^2} - 2BC.AB.\left( { - \frac{1}{2}} \right)\)

\( 196 = B{C^2} + A{B^2} + BC.AB\) (*)

Từ giả thiết ta có: \(BC + AB = 16\) suy ra \(AB = 16 - BC\).

Thay AB = 16 - BC vào (*) ta được:

\(B{C^2} + {(16 - BC)^2} + BC(16 - BC) = 196\)

\(B{C^2} - 16BC + 60 = 0\)

Giải phương trình trên ta được BC = 6 hoặc BC = 10.

Với BC = 10 thì AB = 6 (thỏa mãn yêu cầu đề bài BC > AB).

Với BC = 6 thì AB = 10 (loại vì đề bài yêu cầu BC > AB).

Vậy BC = 10.

Câu 3 :

Cho \(\alpha \) là góc tù và \(\tan \alpha  + \cot \alpha  =  - 2\). Tính giá trị biểu thức \(M = \frac{{\sqrt 2 }}{4}(\sin \alpha  - \cos \alpha )\) (viết kết quả dưới dạng số thập phân).

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Dựa vào hệ thức lượng trong tam giác vuông và giá trị lượng giác của góc tù.

Lời giải chi tiết :

Ta có: \(\tan \alpha  + \cot \alpha  =  - 2\)

\(\frac{{\sin \alpha }}{{\cos \alpha }} + \frac{{\cos \alpha }}{{\sin \alpha }} =  - 2\)

\(\frac{1}{{\sin \alpha \cos \alpha }} =  - 2\)

\(\sin \alpha \cos \alpha  =  - \frac{1}{2}\).

Ta lại có \({(\sin \alpha  - \cos \alpha )^2} = 1 - 2\sin \alpha \cos \alpha  = 1 - 2.\left( { - \frac{1}{2}} \right) = 2\).

Suy ra \(\sin \alpha  - \cos \alpha  =  \pm \sqrt 2 \).

Vì \(\alpha \) là góc tù nên \(\sin \alpha  - \cos \alpha  > 0\). Khi đó \(\sin \alpha  - \cos \alpha  = \sqrt 2 \).

Vậy \(M = \frac{{\sqrt 2 }}{4}(\sin \alpha  - \cos \alpha ) = \frac{{\sqrt 2 }}{4}.\sqrt 2  = \frac{1}{2} = 0,5\).

Câu 4 :

Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 100 kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 5 triệu đồng, có thể chiết xuất được 20 kg chất A. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng có thể chiết xuất được 1,5 kg chất B. Biết mỗi kg chất A có giá 0,5 triệu đồng, mỗi kg chất B có giá 5 triệu đồng. Hỏi phải dùng bao nhiêu tấn nguyên liệu loại I để lợi nhuận thu về là lớn nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 8 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II.

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Lập hệ bất phương trình.

Lời giải chi tiết :

Gọi x, y \((0 \le x \le 8,0 \le y \le 9)\) lần lượt là số tấn nguyên liệu loại I và loại II cần dùng.

Từ x tấn nguyên liệu loại I chiết xuất được 20x kg chất A.

Từ y tấn nguyên liệu loại II chiết xuất được 1,5 kg chất B.

Ta có hệ bất phương trình \(\left\{ \begin{array}{l}20x \ge 100\\1,5y \ge 9\\0 \le x \le 8\\0 \le y \le 9\end{array} \right.\) hay \(\left\{ \begin{array}{l}x \ge 5\\y \ge 6\\0 \le x \le 8\\0 \le y \le 9\end{array} \right.\)

Lợi nhuận thu về là \(F(x;y) = 0,5.20x + 5.1,5y - 5x - 3y = 5x + 4,5y\).

Miền nghiệm biểu diễn là miền tứ giác ABCD có A(5;6), B(8;6), C(8;9), D(5;9).

Tính giá trị của F(x;y) tại các đỉnh A, B, C, D tìm được giá trị lớn nhất là F(8;9) = 80,5.

Vậy cần sử dựng 8 tấn nguyên liệu loại I và 9 tấn nguyên liệu loại II.

Câu 5 :

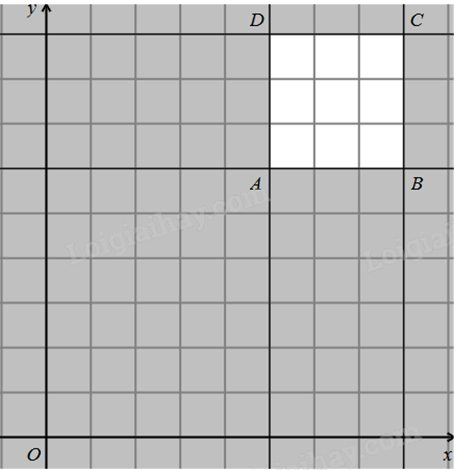
Biểu diễn hình học miền nghiệm (không tô màu) của bất phương trình \(ax + by \le c\) như hình vẽ. Biết rằng \(a,b \in \mathbb{N}*\). Tính a + b.

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Tìm phương trình đường thẳng bờ của miền nghiệm. Thay tọa độ một điểm bất kì vào phương trình đường thẳng vừa tìm để xác định chiều của bất đẳng thức.

Lời giải chi tiết :

Gọi đường thẳng bờ của miền nghiệm là d, có dạng \(y = cx + d\).

Vì điểm (0;3) và \(\left( {\frac{3}{2};0} \right)\) thuộc d nên ta có hệ:

\(\left\{ {\begin{array}{*{20}{c}}{3 = 0c + d}\\{0 = \frac{3}{2}c + d}\end{array}} \right.\) hay \(\left\{ {\begin{array}{*{20}{c}}{d = 3}\\{c =  - 2}\end{array}} \right.\)

Vậy d: \(y =  - 2x + 3\) hay \(2x + y = 3\).

Thay điểm O(0;0) vào phương trình d, ta được: 2.0 + 0 = 0 < 3.

Quan sát hình vẽ thấy O thuộc miền nghiệm nên bất phương trình cần tìm là \(2x + y \le 3\).

Suy ra a = 2, b = 1. Vậy a + b = 2 + 1 = 3.

Câu 6 :

Một nhóm có 12 học sinh chuẩn bị cho hội diễn văn nghệ. Trong danh sách đăng kí tham gia tiết mục múa và tiết mục hát của nhóm đó, có 5 học sinh tham gia tiết mục múa, 3 học sinh tham gia cả hai tiết mục. Hỏi có bao nhiêu học sinh trong nhóm tham gia tiết mục hát? Biết có 4 học sinh của nhóm không tham gia tiết mục nào.

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Sử dụng kiến thức về các phép toán trên tập hợp.

Nếu A và B là hai tập hợp hữu hạn thì \(n(A \cup B) = n(A) + n(B) - n(A \cap B)\).

Lời giải chi tiết :

Cách 1:

Gọi A là tập hợp các học sinh tham gia tiết mục múa, B là tập hợp các học sinh tham gia tiết mục hát.

Khi đó, số phần tử của hai tập hợp A, B là \(n(A) = 5\) và \(n(B)\).

Số học sinh tham gia ít nhất một trong hai tiết mục là \(n(A \cup B) = 12 - 4 = 8\) (vì có 4 học sinh không tham gia tiết mục nào).

Theo đề bài, số học sinh tham gia cả hai tiết mục là \(n(A \cap B) = 5\).

Ta có: \(n(A \cup B) = n(A) + n(B) - n(A \cap B)\)

\(8 = 5 + n(B) - 3\)

\(n(B) = 6\).

Vậy có 6 học sinh tham gia tiết mục hát.

Cách 2:

Vì nhóm có 12 học sinh, trong đó 4 học sinh không tham gia tiết mục nào nên tổng số học sinh tham gia hai tiết mục múa và hát là 12 – 4 = 8 (học sinh).

Trong 5 học sinh tham gia tiết mục múa, có 3 học sinh tham gia cả hai tiết mục nên số học sinh chỉ tham gia tiết mục múa là 5 – 3 = 2 (học sinh).

Do đó, số học sinh tham gia tiết mục hát là 8 – 2 = 6 (học sinh).

Bài liên quan
close