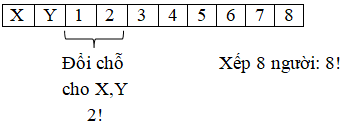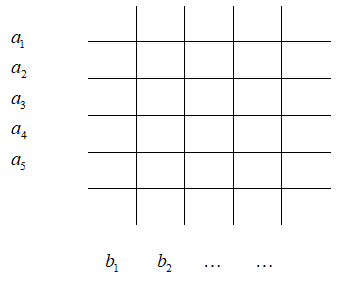Phương pháp giải:

Do ở đây việc tìm trực tiếp sẽ có nhiều trường hợp nên ta sẽ giải quyết bài toán bằng cách gián tiếp, ta sẽ đi tìm bài toán đối. Ta tìm số cách chọn ra $5$ bạn mà trong đó có cả bạn Thùy và Thiện.

Lời giải chi tiết:

Bài toán đối: tìm số cách chọn ra $5$ bạn mà trong đó có cả bạn Thùy và Thiện.

Bước 1: Chọn nhóm $3$ em trong $13$ em ($13$ em này không tính em Thùy và Thiện) có $C_{13}^3 = 286$ cách.

Bước 2: Chọn $2$ em Thùy và Thiện có 1 cách.

Vậy theo quy tắc nhân thì ta có $286$ cách chọn $5$ em mà trong đó có cả $2$ em Thùy và Thiện.

Chọn $5$ em bất kì trong số $15$ em thì ta có: $C_{15}^5 = 3003$ cách.

Vậy theo yêu cầu đề bài thì có tất cả $3003-286 = 2717$ cách chọn mà trong đó có ít nhất một trong hai em Thùy Và Thiện không được chọn.

Chọn C.

Phương pháp giải:

Sử dụng nguyên tắc vách ngăn: Xếp chữ số $5$ trước để tạo ra các vách ngăn sau đó xếp các chữ số $2$ vào các vách ngăn đó

Lời giải chi tiết:

TH1: Có $10$ chữ số $5$: Chỉ có duy nhất $1$ số.

TH2: Có $9$ chữ số $5$ và $1$  chữ số $2$.

Xếp $9$ chữ số $5$  thành 1 hàng ngang có 1 cách. Khi đó ta sẽ tạo nên 10 vách ngăn. Việc còn lại là xếp 1 chữ số 2 vào 10 vách ngăn đó, có 10 cách. Vậy trường hợp này có 10 số.

TH3: Có $8$ chữ số $5$ và $2$  chữ số $2$.

Xếp 8 chữ số 5 thành 1 hàng ngang có 1 cách. Khi đó ta sẽ tạo nên 9 vách ngăn. Việc còn lại là xếp 2 chữ số 2 vào $9$ vách ngăn đó, có

$C_9^2 = 36$  cách.

Vậy trường hợp này có 36 số.

TH4: Có $7$ chữ số $5$  và $3$ chữ số $2$ .

Xếp 7 chữ số 5 thành 1 hàng ngang có 1 cách. Khi đó ta sẽ tạo nên 8 vách ngăn. Việc còn lại là xếp 3 chữ số 2 vào 8 vách ngăn đó, có

$C_8^3 = 56$  cách.

Vậy trường hợp này có 56 số.

TH5: Có $6$ chữ số $5$ và $4$ chữ số $2$ .

Xếp 6 chữ số 5 thành 1 hàng ngang có 1 cách. Khi đó ta sẽ tạo nên 7 vách ngăn. Việc còn lại là xếp 4 chữ số 2 vào 7 vách ngăn đó, có

$C_7^4 = 35$  cách.

Vậy trường hợp này có 35 số.

TH6: Có $5$ chữ số $5$  và $5$ chữ số $2$.

Xếp 5 chữ số 5 thành 1 hàng ngang có 1 cách. Khi đó ta sẽ tạo nên 6 vách ngăn. Việc còn lại là xếp 5 chữ số 2 vào 6 vách ngăn đó, có

$C_6^5 = 6$  cách.

Vậy trường hợp này có 6 số.

Theo quy tắc cộng ta có tất cả:

$1 + 10 + 36 + 56 + 35 + 6 = 144$ số.

Chọn A.

Phương pháp giải:

- Gọi số tạo thành có dạng $x = \overline {abc}$, với $a$, $b$, $c$ đôi một khác nhau và lấy từ $A$.

- Chọn vị trí cho chữ số 3.

- Chọn 2 chữ số còn lại. Áp dụng quy tắc nhân.

Lời giải chi tiết:

Gọi số tạo thành có dạng $x = \overline {abc}$, với $a$, $b$, $c$ đôi một khác nhau và lấy từ $A$.

Chọn một vị trí $a,\,\,b$ hoặc $c$ cho số $3$ có $3$ cách chọn.

Chọn hai chữ số khác $3$ từ $A$ và sắp xếp vào hai vị trí còn lại của $x$ có $A_4^2$ cách chọn

Theo quy tắc nhân có $3.A_4^2 = 36$ cách chọn

Mỗi cách sắp xếp như trên cho ta một số thỏa yêu cầu.

Vậy có $36$ số cần tìm.

Chọn B.

Phương pháp giải:

- Liệt kê các trường hợp có tổng 4 số bằng 7, chia các trường hợp sau:

   + Trong 4 chữ số a, b, c, d có 3 chữ số bằng 0.

   + Trong 4 chữ số a, b, c, d có 2 chữ số bằng 0.

   + Trong 4 chữ số a, b, c, d có 1 chữ số bằng 0.

   + Trong 4 chữ số a, b, c, d có 0 chữ số bằng 0.

- Sử dụng hoán vị sau đó áp dụng quy tắc cộng.

Lời giải chi tiết:

Gọi số cần tìm có dạng $\overline {abcd}$ $\left( {a,\,\,b,\,\,c,\,\,d \in \mathbb{N},\,\,0 \le a,\,\,b,\,\,c,\,\,d \le 9,\,\,a \ne 0} \right)$.

TH1: Trong 4 chữ số a, b, c, d có 3 chữ số bằng 0 $\Rightarrow b = c = d = 0,\,\,a = 7$.

Do đó có 1 số thỏa mãn.

TH2: Trong 4 chữ số a, b, c, d có 2 chữ số bằng 0.

- Chọn vị trí cho 2 chữ số 0 có $C_3^2 = 3$ cách.

- Tổng hai chữ số còn lại là 7, ta có $7 = 6 + 1 = 5 + 2 = 4 + 3 = 3 + 4 = 2 + 5 = 1 + 6$ nên có 6 cách chọn 2 chữ số còn lại.

Do đó trường hợp này có 18 số.

TH3: Trong 4 chữ số a, b, c, d có 1 chữ số bằng 0.

- Chọn vị trí cho 1 chữ số 0 có $C_3^1 = 3$ cách.

- Tổng 3 chữ số còn lại bằng 7, ta có: $7 = 1 + 1 + 5 = 1 + 2 + 4 = 1 + 3 + 3 = 2 + 2 + 3$.

   + Với bộ số (1;2;4) có $3! = 6$ cách chọn 3 chữ số còn lại.

   + Với 3 bộ số còn lại có $\dfrac{{3!}}{{2!}} = 3$ cách chọn 3 chữ số còn lại.

Do đó trường hợp này có $3.\left( {6 + 3.3} \right) = 45$ số.

TH4: Trong 4 chữ số a, b, c, d  không có chữ số nằm bằng 0.

Ta có: $\left\{ \begin{array}{l}7 = 1 + 1 + 1 + 4\\7 = 1 + 1 + 2 + 3\\7 = 1 + 2 + 2 + 2\end{array} \right.$.

   + Với bộ số (1;1;1;4), có $\dfrac{{4!}}{{3!}} = 4$ cách chọn 4 chữ số a, b, c, d.

   + Với bộ số (1;1;2;3), có $\dfrac{{4!}}{{2!}} = 12$ cách chọn 4 chữ số a, b, c, d.

   + Với bộ số (1;2;2;2), có $\dfrac{{4!}}{{3!}} = 4$ cách chọn 4 chữ số a, b, c, d.

Do đó trường hợp này có 4 + 12 + 4 = 20 số thỏa mãn.

Vậy có tất cả:  1 + 18 + 45 + 20 = 84 số.

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

$A_n^3 + C_n^{n - 2} = 14n$$\left\{ \begin{array}{l}n \ge 3\\n \in N\end{array} \right.$

$\Leftrightarrow \dfrac{{n!}}{{\left( {n - 3} \right)!}} + \dfrac{{n!}}{{\left( {n - 2} \right)!.2!}} = 14n$

$\Leftrightarrow \left( {n - 2} \right)\left( {n - 1} \right)n + \dfrac{{\left( {n - 1} \right)n}}{{2!}} = 14n$

$\Leftrightarrow \left( {n - 2} \right)\left( {n - 1} \right) + \dfrac{{n - 1}}{2} = 14$ (Chia 2 vế cho n vì $n \ne 0$)

$\Leftrightarrow 2{n^2} - 5n - 25 = 0$

$\Leftrightarrow \left[ \begin{array}{l}n = 5\,\,\,\,\,\,\,\,\,\,\left( {tm} \right)\\n =  - 2,5\,\,\,\left( {ktm} \right)\end{array} \right.$

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

$C_n^5 < C_n^3$$\left( {n \ge 5;\,\,n \in N} \right)$

$\Leftrightarrow C_n^5 - C_n^3 < 0$

$\Leftrightarrow \dfrac{{n!}}{{5!\left( {n - 5} \right)!}} - \dfrac{{n!}}{{3!\left( {n - 3} \right)!}} < 0$

$\Leftrightarrow \dfrac{{\left( {n - 4} \right)\left( {n - 3} \right)\left( {n - 2} \right)\left( {n - 1} \right)n}}{{120}} - \dfrac{{\left( {n - 2} \right)\left( {n - 1} \right)n}}{6} < 0$

$\Leftrightarrow \dfrac{{\left( {n - 4} \right)\left( {n - 3} \right)\left( {n - 2} \right)\left( {n - 1} \right)n - 20\left( {n - 2} \right)\left( {n - 1} \right)n}}{{120}} < 0$

$\Leftrightarrow \left( {n - 2} \right)\left( {n - 1} \right)n.\left[ {\left( {n - 4} \right)\left( {n - 3} \right) - 20} \right] < 0$

Mà $n \ge 5$$\Rightarrow \left( {n - 2} \right)\left( {n - 1} \right)n > 0$

$\Leftrightarrow \left( {n - 4} \right)\left( {n - 3} \right) - 20 < 0$

$\Leftrightarrow {n^2} - 7n + 12 - 20 < 0$

$\Leftrightarrow {n^2} - 7n - 8 < 0$

$\Leftrightarrow \left\{ \begin{array}{l} - 1 < n < 8\\n \ge 5\end{array} \right. \Rightarrow 5 \le n < 8$

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

ĐK: $n \ge 1$

$C_n^{n - 2} - 2C_n^1 \le 18$

$\Leftrightarrow \dfrac{{n!}}{{\left( {n - 2} \right)!.2!}} - 2\dfrac{{n!}}{{1!\left( {n - 1} \right)!}} \le 18$

$\Leftrightarrow \dfrac{{n\left( {n - 1} \right)}}{2} - 2n \le 18$

$\Leftrightarrow n\left( {n -1 } \right) - 4n \le 36$

$\Leftrightarrow {n^2} - n - 4n - 36 \le 0$

$\Leftrightarrow {n^2} - 5n - 36 \le 0$

$\Leftrightarrow  - 4 \le n \le 9$

Kết hợp $n \ge 1$$\Rightarrow n \in \left[ {1;9} \right]$

Vậy tổng các nghiệm là: $\dfrac{{(1 + 9).9}}{2} = 45$$\Rightarrow S = 45$ .

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

ĐK: $n \ge 6$

$C_n^{n - 3} = 1140$

$\Leftrightarrow \dfrac{{n!}}{{\left( {n - 3} \right)!.3!}} = 1140$

$\Leftrightarrow \dfrac{{n\left( {n - 1} \right)\left( {n - 2} \right)}}{6} = 1140$

$\Rightarrow n = 20$

$+ )\,\,\,A = \dfrac{{A_n^6 + A_n^5}}{{A_n^4}} = \dfrac{{A_{20}^6 + A_{20}^5}}{{A_{20}^4}} = 256$.

Chọn A.

Phương pháp giải:

Sử dụng bài toán chia kẹo Euler.

Lời giải chi tiết:

Xếp 20 chiếc bút chì giống nhau trên thành 1 hàng ngang, khi đó, giữa các chiếc bút có 19 khe. Ta chọn vị trí và đặt 2 vách ngăn vào 2 vị trí khe (2 khe khác nhau). Hai vách ngăn sẽ chia 20 chiếc bút thành 3 phần, ứng với  số bút mà 3 bạn Trung, Việt, Phi tương ứng nhận được.

Số cách chọn đó là: $C_{19}^2 = 171$.

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

$A_x^{10} + A_x^9 = 9A_x^8$  $\left( {x \ge 10;\,\,x \in {N^*}} \right)$

$\Leftrightarrow \dfrac{{x!}}{{\left( {x - 10} \right)!}} + \dfrac{{x!}}{{\left( {x - 9} \right)!}} = 9\dfrac{{x!}}{{\left( {x - 8} \right)!}}$

$\Leftrightarrow x\left( {x - 1} \right)\left( {x - 2} \right)...\left( {x - 9} \right) + x\left( {x - 1} \right)\left( {x - 2} \right)...\left( {x - 8} \right) = 9x\left( {x - 1} \right)\left( {x - 2} \right)...\left( {x - 7} \right)$

$\Leftrightarrow \left( {x - 8} \right)\left( {x - 9} \right) + \left( {x - 8} \right) = 9$

$\Leftrightarrow {x^2} - 9x - 8x + 72 + x - 8 - 9 = 0$

$\Leftrightarrow {x^2} - 16x + 55 = 0$

$\Leftrightarrow \left[ \begin{array}{l}x = 11\,\,\,\,\left( {tm} \right)\\x = 5\,\,\,\,\,\left( {ktm} \right)\end{array} \right.$ .

Chọn B.

Phương pháp giải:

Lời giải chi tiết:

$A_n^2 + C_{n + 1}^{n - 1} = 4n + 6$  $\left( {n \ge 2;\,\,n \in N} \right)$

$\Leftrightarrow \dfrac{{n!}}{{\left( {n - 2} \right)!}} - \dfrac{{\left( {n + 1} \right)!}}{{2\left( {n - 1} \right)!}} = 4n + 6$

$\Leftrightarrow n\left( {n - 1} \right) - \dfrac{{n\left( {n + 1} \right)}}{2} = 4n + 6$

$\Leftrightarrow 2n\left( {n - 1} \right) - n\left( {n + 1} \right) - 8n - 12 = 0$

$\Leftrightarrow 2{n^2} - 2n - {n^2} - n - 8n - 12 = 0$

$\Leftrightarrow {n^2} - 11n - 12 = 0$

$\Leftrightarrow \left[ \begin{array}{l}n = 12\,\,\,\left( {tm} \right)\\n =  - 1\,\,\,\left( {ktm} \right)\end{array} \right.$

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

Số tập con gồm 4 phần tử của A bằng 20 lần số tập con gồm 2 phần tử của A nên

Ta có phương trình:$C_n^4 = 20C_n^2$

$\Leftrightarrow \dfrac{{n!}}{{4!\left( {n - 4} \right)!}} = 20\dfrac{{n!}}{{2!\left( {n - 2} \right)!}}$

$\Leftrightarrow \dfrac{{n\left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right)}}{{24}} = \dfrac{{20n\left( {n - 1} \right)}}{2}$

$\begin{array}{l} \Leftrightarrow \dfrac{{n\left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right)}}{{24}} - \dfrac{{20n\left( {n - 1} \right)}}{2} = 0\\ \Rightarrow n.\left( {n - 1} \right).\left[ {\dfrac{{\left( {n - 2} \right)\left( {n - 3} \right)}}{{24}} - 10} \right] = 0\end{array}$

$\Leftrightarrow \left[ \begin{array}{l}n = 0\\n = 1\\\dfrac{{\left( {n - 2} \right)\left( {n - 3} \right)}}{{24}} = 10\end{array} \right.$ (Vì $n \ge 4$$\Rightarrow n = 0,\,\,n = 1$ loại)

$\Leftrightarrow {n^2} - 2n - 3n + 6 - 240 = 0$

$\Leftrightarrow {n^2} - 5n - 234 = 0$

$\Rightarrow \left[ \begin{array}{l}n = 18\,\,\,\,\,\,\left( {tm} \right)\\n =  - 13\,\,\left( {ktm} \right)\end{array} \right.$

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

$C_{n + 4}^{n + 1} - C_{n + 3}^n = 7\left( {n + 3} \right)$$\left( {n \in N} \right)$

Có tính chất: $C_n^k = C_n^{n - k}$$\Rightarrow \left\{ \begin{array}{l}C_{n + 4}^{n + 1} = C_{n + 4}^3\\C_{n + 3}^n = C_{n + 3}^3\end{array} \right.$

$\Leftrightarrow C_{n + 4}^3 - C_{n + 3}^3 = 7\left( {n + 3} \right)$

$\Leftrightarrow \dfrac{{\left( {n + 4} \right)!}}{{3!.\left( {n + 1} \right)!}} - \dfrac{{\left( {n + 3} \right)!}}{{3!.n!}} = 7\left( {n + 3} \right)$

$\Leftrightarrow \dfrac{{\left( {n + 2} \right)\left( {n + 3} \right)\left( {n + 4} \right)}}{{3!}} - \dfrac{{\left( {n + 1} \right)\left( {n + 2} \right)\left( {n + 3} \right)}}{{3!}} = 7\left( {n + 3} \right)$

$\Leftrightarrow \left[ \begin{array}{l}n + 3 = 0 \Leftrightarrow n =  - 3\,\,(Loai)\\\dfrac{{\left( {n + 2} \right)\left( {n + 4} \right)}}{{3!}} - \dfrac{{\left( {n + 1} \right)\left( {n + 2} \right)}}{{3!}} = 7\end{array} \right.$

$\Leftrightarrow \left( {n + 2} \right)\left( {n + 4} \right) - \left( {n + 1} \right)\left( {n + 2} \right) = 42$

$\Leftrightarrow 3n + 6 = 42$

$\Leftrightarrow n = 12$

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

ĐK: $n \le 5;\,\,n \in N$

$\dfrac{5}{{C_5^n}} - \dfrac{2}{{C_6^n}} = \dfrac{{14}}{{C_7^n}}$

$\Leftrightarrow \dfrac{{5.n!.\left( {5 - n} \right)!}}{{5!}} - \dfrac{{2.n!.\left( {6 - n} \right)!}}{{6!}} = \dfrac{{14.n!.\left( {7 - n} \right)!}}{{7!}}$

$\Leftrightarrow \dfrac{5}{{5!}} - \dfrac{{2\left( {6 - n} \right)}}{{6!}} = \dfrac{{14\left( {6 - n} \right)\left( {7 - n} \right)}}{{7!}}$

$\Leftrightarrow 5 - \dfrac{{6 - n}}{3} = \dfrac{{\left( {6 - n} \right)\left( {7 - n} \right)}}{3}$ (Nhân 2 vế với 5!)

$\Leftrightarrow 15 - \left( {6 - n} \right) = \left( {6 - n} \right).\left( {7 - n} \right)$

$\Leftrightarrow {n^2} - 14n + 33 = 0$

$\Leftrightarrow \left[ \begin{array}{l}n = 3\,\,\,\,\,\,\left( {tm} \right)\\n = 11\,\,\left( {ktm} \right)\end{array} \right.$

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

+ Coi X,Y là 1 vị trí $\Rightarrow$ Có 9 cách xếp vị trí cho X,Y

$\Rightarrow$ Vậy tổng cộng có: $9 \times 2! \times 8! = 2! \times 9!$

Chọn B.

Phương pháp giải:

Lời giải chi tiết:

TH1:

B

G

B

G

B

G

B

G

B

G

               Chọn chỗ cho 5 bạn nam: 5! ( xếp 5 bạn vào 5 vị trí B)

               Chọn chỗ cho 5 bạn nữ: 5!    ( xếp 5 bạn vào 5 vị trí G)

               $\Rightarrow$ $5!\, \times 5!$

TH2:

G

B

G

B

G

B

G

B

G

B

                       Tương tự: $5!\, \times 5!$

               $\Rightarrow$ Có $2 \times {(5!)^2}$ cách xếp.

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

4 cách

Ta thấy HBH được tạo ra khi chọn 2 đường thẳng a và 2 đường thẳng b

Chọn 2 đường a: $C_5^2$

Chọn 2 đường b: $C_7^2$

 $\Rightarrow$ $C_5^2$ $\times$ $C_7^2$ 

Chọn B.

Phương pháp giải:

Lời giải chi tiết:

Xếp 30 tập thành 1 hàng $\Rightarrow 30!$ cách xếp

            + Tập 1 và 2 đứng kề nhau: 2! Cách xếp

            + Coi tập 1 và tập 2 là một vị trí $\Rightarrow$ Có 29 vị trí xếp sao cho tập 1,2 kề nhau

            + Xếp 28 quyển còn lại vào giá ta có: $28!$ cách xếp

Vậy số cách xếp tập 1 và 2 kề nhau là: $2!.29.28! = 2!.29!$

+ Vậy số cách xếp mà tập 1 và 2 không đứng kề nhau = Tổng cách xếp ­$- \,2!\, \times \,29!$= $30!\, - 2!\, \times 29!$= $28 \times 29!$

Chọn B.

Phương pháp giải:

Số chia hết cho 6 là số chia hết cho 2 và cho 3.

Lời giải chi tiết:

Đặt $A = \left\{ {0;1;2;3;4;5;6} \right\}$.

Gọi số tự nhiên có 5 chữ số đôi một khác nhau là $X = \overline {abcde} \,\,\left( {a \ne 0,\,\,a,b,c,d,e \in A} \right)$.

Vì $X\,\, \vdots \,\,6$ nên $X\,\, \vdots \,\,2$ và $X\,\, \vdots \,\,3$.

TH1: $d = 0$. Khi đó $a + b + c + d\,\, \vdots \,\,3$.

$\Rightarrow \left( {a,b,c,d} \right) \in \left\{ {\left( {3;6;1;2} \right);\left( {3;6;1;5} \right);\left( {3;6;4;2} \right);\left( {3;6;4;5} \right);\left( {1;2;4;5} \right)} \right\}$.

$\Rightarrow$ Có $5.4! = 120$ số chia hết cho 6.

TH2: $e = 2 \Rightarrow a + b + c + d$ chia 3 dư 1.

$\Rightarrow \left( {a;b;c;d} \right) \in \left\{ {\left( {0;3;6;1} \right);\left( {0;3;6;4} \right);\left( {0;1;4;5} \right);\left( {1;3;4;5} \right);\left( {1;4;5;6} \right)} \right\}$.

$\Rightarrow$ Có $3\left( {4! - 3!} \right) + 2.4! = 102$ số.

TH3: $e = 4 \Rightarrow a + b + c + d$ chia 3 dư 2.

$\Rightarrow \left( {a;b;c;d} \right) \in \left\{ {\left( {0;3;6;2} \right);\left( {0;3;6;5} \right);\left( {0;1;2;5} \right);\left( {3;1;2;5} \right);\left( {6;1;2;5} \right)} \right\}$.

$\Rightarrow$ Có $3\left( {4! - 3!} \right) + 2.4! = 102$ số.

TH4: $e = 6 \Rightarrow a + b + c + d$ chia 3.

$\Rightarrow \left( {a,b,c,d} \right) \in \left\{ {\left( {0;3;1;2} \right);\left( {0;3;1;5} \right);\left( {0;3;4;2} \right);\left( {0;3;4;5} \right);\left( {1;2;4;5} \right)} \right\}$.

$\Rightarrow$ Có $4\left( {4! - 3!} \right) + 4! = 96$ số.

Vậy có tất cả $120 + 102 + 102 + 96 = 420$ số.

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

+ Gọi số có 3 chữ số khác nhau có dạng: $\overline {abc}$

+ Để số có 3 chữ số chia hết cho 9 $\Rightarrow$ Tổng $a + b + c$ phải chia hết cho 9

+ Tập hợp các số mà tổng của chúng chia hết cho 9 là:

$A = \left\{ {0,5,4} \right\}$$\Rightarrow$ Các số đó là: $540,450,504,405$ $\Rightarrow$ Vậy có 4

$B = \left\{ {2,3,4} \right\}$$\Rightarrow$ Đảo vị trí 3 số ta có: $3!$

$C = \left\{ {1,3,5} \right\}$$\Rightarrow$ Đảo vị trí 3 số ta có: $3!$

Vậy có: $4 + 3! + 3! = 16$ số

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

Ta phân các trường hợp như sau

TH1:

T

T

T

T

T

V

V

V

V

V

+ Xếp 5 quyển toán vào 5 chỗ$\Rightarrow$ Có 5! Cách

+ Xếp 5 quyển văn vào 5 chỗ$\Rightarrow$ Có 5! Cách

$\Rightarrow$ Có: $5!.5!$ cách

TH2:  

V

V

V

V

V

T

T

T

T

T

+ Xếp 5 quyển toán vào 5 chỗ$\Rightarrow$ Có 5! Cách

+ Xếp 5 quyển văn vào 5 chỗ$\Rightarrow$ Có 5! Cách

$\Rightarrow$ Có: $5!.5!$ cách

Vậy có tổng cộng: $2.5!.5!$ cách xếp

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

Tập các số tự nhiên là $0,1,2,3,4,5,6,7,8,9.$

+ Gọi số có 9 chữ số khác nhau cần lập là: $\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}{a_7}{a_8}{a_9}}$

+ Số các số tự nhiên có 9 chữ số khác nhau là $9 \times 9!$
+ Ta sẽ lập ra số có 9 chữ số mà có chữ số 0 hoặc 1 đứng giữa

TH1: Số 0 đứng giữa $\Rightarrow {a_5} = 0$$\Rightarrow$ 1 cách

0

$\Rightarrow$ Lập 8 số còn lại ta có: 9! Cách

TH1: Số 1 đứng giữa $\Rightarrow {a_5} = 1$$\Rightarrow$ 1 cách

1

$\Rightarrow$ Lập 8 số còn lại ta có: 8.8! cách

$\Rightarrow$ Có tổng cộng: $9! + 8.8!$ số

Vậy Số các số tự nhiên có 9 chữ số khác nhau mà số 1 hoặc 0 không đứng giữa là: $9 \times 9!$$- \left( {9! + 8.8!} \right) = {8^2}.8!$

Chọn B

Phương pháp giải:

Sử dụng tổ hợp.

Lời giải chi tiết:

+) Trong 6 học sinh có 5 học sinh nam, 1 học sinh nữ$\Rightarrow \left| {{\Omega _A}} \right| = C_{20}^5.C_{15}^1$

+) Cả 6 học sinh được chọn đều là nam  $\Rightarrow \left| {{\Omega _A}} \right| = C_{20}^6$

Vậy tổng có $C_{20}^6 + C_{20}^5.C_{15}^1 = 271320$ cách chọn thỏa mãn đề bài.

Chọn B.

Phương pháp giải:

- Đếm các số chẵn có $5$ chữ số khác nhau mà có đúng hai chữ số lẻ.

- Đếm các số chẵn có $5$ chữ số khác nhau mà có hai chữ số lẻ đứng cạnh nhau.

- Trừ các kết quả cho nhau ta dược đáp số.

Lời giải chi tiết:

Gọi số có năm chữ số có dạng $\overline {abcde}$.

TH1: $e = 0$ có $1$ cách chọn.

Chọn $2$ chữ số lẻ và $2$ chữ số chẵn và xếp vị trí cho chúng có $C_5^2.C_4^2.4!$ cách chọn.

Do đó có  $C_5^2.C_4^2.4!$ số.

TH2: $e \in \left\{ {2;4;6;8} \right\}$ có $4$ cách chọn.

+) Nếu $a$ chẵn, $a \ne 0,a \ne e$ thì có $3$ cách chọn.

Số cách chọn 3 chữ số còn lại ($1$ chữ số chẵn và $2$ chữ số lẻ) và xếp vị trí cho chúng là $C_3^1.C_5^2.3!$ cách chọn.

Do đó có $3.C_3^1.C_5^2.3!$ số.

+) Nếu $a$ lẻ thì có $5$ cách chọn.

Số cách chọn 3 chữ số còn lại ($2$ chữ số chẵn và $1$ chữ số lẻ) và xếp vị trí cho chúng là $C_4^2.C_4^1.3!$ cách chọn.

Do đó có $5.C_4^2.C_4^1.3!$ số.

Khi đó số các số chẵn có $5$ chữ số khác nhau mà chỉ có đúng $2$ chữ số lẻ là $C_5^2.C_4^2.4! + 4.\left( {3.C_3^1.C_5^2.3! + 5.C_4^2.C_4^1.3!} \right) = 6480$ số.

Ta tính số các số chẵn có $5$ chữ số khác nhau chỉ có $2$ chữ số lẻ mà chúng đứng cạnh nhau.

Coi hai chữ số lẻ đứng cạnh nhau là một chữ số $A$, có $A_5^2$ cách chọn và sắp xếp vị trí của hai chữ số trong $A$.

Số có dạng $\overline {abcd}$ với $a,b,c,d \in \left\{ {A;0;2;4;6;8} \right\}$.

+) Nếu $a = A$ thì có $A_5^3$ cách chọn $b,c,d$.

+) Nếu $a \ne A,a \ne 0$ thì có $4$ cách chọn.

$A$ có thể đứng ở vị trí $b$ hoặc $c$ nên có $2$ cách xếp.

Có $A_4^2$ cách chọn và sắp xếp hai chữ số còn lại.

Do đó có $A_5^2\left( {A_5^3 + 4.2.A_4^2} \right) = 3120$

Vậy có $6480 - 3120 = 3360$ số.

Phương pháp giải:

Xét 2 TH:

TH1: ${a_1} < {a_2} < {a_3} < {a_4} < {a_5}$.

TH2: ${a_1} < {a_2} < {a_3} = {a_4} < {a_5}$

Sử dụng tổ hợp và quy tắc cộng.

Lời giải chi tiết:

TH1: ${a_1} < {a_2} < {a_3} < {a_4} < {a_5}$.

Do ${a_1} \ne 0 \Rightarrow 0 < {a_1} < {a_2} < {a_3} < {a_4} < {a_5}$.

Chọn 5 chữ số từ 9 chữ số $\left\{ {1;2;3;...;9} \right\}$ có $C_9^5 = 126$ cách chọn. Ứng với mỗi cách chọn có duy nhất 1 cách xếp các số đó theo thứ tự tăng dần.

$\Rightarrow$ Có 126 số.

TH2: ${a_1} < {a_2} < {a_3} = {a_4} < {a_5}$

Do ${a_1} \ne 0 \Rightarrow 0 < {a_1} < {a_2} < {a_3} = {a_4} < {a_5}$.

Chọn 4 chữ số từ 9 chữ số $\left\{ {1;2;3;...;9} \right\}$ có $C_9^4 = 126$ cách chọn. Ứng với mỗi cách chọn có duy nhất 1 cách xếp các số đó theo thứ tự tăng dần.

$\Rightarrow$ Có 126 số.

Vậy có tất cả $126 + 126 = 252$ số thỏa mãn.

Chọn A.

Phương pháp giải:

Sử dụng phương pháp vách ngăn.

Lời giải chi tiết:

Xếp 4 số lẻ có $4!$ cách xếp, khi đó tạo ra 5 vách ngăn giữa các số lẻ (Kể cả 2 vách ngăn ở đầu).

VD: _1_3_5_7_ (_ là các vách ngăn).

Chọn 3 trong 5 vách ngăn để xếp 3 số chẵn, có $A_5^3 = 3.4.5$ cách.

Vậy có $4!.3.4.5 = 4!.5.6.2 = 2.6!$ số thỏa mãn.

Chọn B.

Phương pháp giải:

- Để một số chia hết cho 15 thì số đó phải chia hết cho 3 và cho 5.

- Xét các trường hợp sau:

   TH1: $d = 0$, số cần tìm có dạng $\overline {abc0}$.

             + $a,\,\,b,\,\,c \equiv 3\,\,\left( {\bmod 1} \right) \Rightarrow a,\,\,b,\,\,c \in \left\{ {1;4;7} \right\}$.

             + $a,\,\,b,\,\,c \equiv 3\,\,\left( {\bmod 2} \right) \Rightarrow a,\,\,b,\,\,c \in \left\{ {2;5;8} \right\}$.

             + Trong 3 số $a,\,\,b,\,\,c$ có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2.

   TH2: $d = 5$, số cần tìm có dạng $\overline {abc5}$.

             + Trong 3 số $a,\,\,b,\,\,c$ có 2 số chia hết cho 3, 1 số chia 3 dư 1.

             + Trong 3 số $a,\,\,b,\,\,c$ có 1 số chia hết cho 3, 2 số chia 3 dư 3.

             + Trong 3 số $a,\,\,b,\,\,c$ có 1 số chia 3 dư 1, 1 số chia 3 dư 2.

Lời giải chi tiết:

Gọi số tự nhiên có 4 chữ số khác nhau là $\overline {abcd} \,\,\left( {a \ne 0} \right)$.

Để một số chia hết cho 15 thì số đó phải chia hết cho 3 và cho 5.

$\Rightarrow d \in \left\{ {0;5} \right\}$.

TH1: $d = 0$, số cần tìm có dạng $\overline {abc0}$.

Để số cần tìm chia hết cho 3 thì $a + b + c\,\, \vdots \,\,3$.

Ta có các nhóm: $\left\{ \begin{array}{l}9\,\, \equiv \,\,3\left( {\bmod 0} \right)\\\left\{ {1;4;7} \right\} \equiv 3\,\,\left( {\bmod 1} \right)\\\left\{ {2;5;8} \right\} \equiv 3\,\,\left( {\bmod 2} \right)\end{array} \right.$

+ $a,\,\,b,\,\,c \equiv 3\,\,\left( {\bmod 1} \right) \Rightarrow a,\,\,b,\,\,c \in \left\{ {1;4;7} \right\}$.

$\Rightarrow$ Có $3!$ cách chọn.

+ $a,\,\,b,\,\,c \equiv 3\,\,\left( {\bmod 2} \right) \Rightarrow a,\,\,b,\,\,c \in \left\{ {2;5;8} \right\}$.

$\Rightarrow$ Có $3!$ cách chọn.

+ Trong 3 số $a,\,\,b,\,\,c$ có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2.

$\Rightarrow$ Có $1.C_3^1.C_3^1.3!$ cách chọn.

$\Rightarrow$ Có $3! + 3! + 1.C_3^1.C_3^1.3! = 66$ số.

TH2: $d = 5$, số cần tìm có dạng $\overline {abc5}$.

Để số cần tìm chia hết cho 3 thì $a + b + c + 5\,\, \vdots \,\,3$, trong đó $5 \equiv 3\,\,\left( {\bmod 2} \right)$.

Ta có các nhóm: $\left\{ \begin{array}{l}\left\{ {0;9} \right\}\,\, \equiv \,\,3\left( {\bmod 0} \right)\\\left\{ {1;4;7} \right\} \equiv 3\,\,\left( {\bmod 1} \right)\\\left\{ {2;8} \right\} \equiv 3\,\,\left( {\bmod 2} \right)\end{array} \right.$

+ Trong 3 số $a,\,\,b,\,\,c$ có 2 số chia hết cho 3, 1 số chia 3 dư 1.

$\Rightarrow$ Có $C_3^1.3! - C_1^3.2! = 12$ cách chọn.

+ Trong 3 số $a,\,\,b,\,\,c$ có 1 số chia hết cho 3, 2 số chia 3 dư 3.

$\Rightarrow$ Có $C_2^1.3! - 2! = 10$ cách chọn.

+ Trong 3 số $a,\,\,b,\,\,c$ có 1 số chia 3 dư 1, 1 số chia 3 dư 2.

$\Rightarrow$ Có $C_3^2.C_2^1.3! = 36$ cách chọn.

Vậy có tất cả $66 + 12 + 10 + 36 = 124$ số thỏa mãn.

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

TH1: Số 3 và số 4 có mặt 2 lần, số 5 và 6 có mặt 0 lần $\Rightarrow$ Có $C_4^2.C_2^2 = 6$ số.

TH2: Số 3 có mặt 2 lần, số 4 có mặt 1 lần, số 5 có mặt 1 lần, số 6 có mặt 0 lần $\Rightarrow$ Có $C_4^2.C_2^1 = 12$ số.

TH tương tự TH2:

+) Số 3 có mặt 2 lần, số 4 có mặt 1 lần, số 5 có mặt 0 lần, số 6 có mặt 1 lần.

+) Số 4 có mặt 2 lần, số 3 có mặt 1 lần, số 5 có mặt 1 lần, số 6 có mặt 0 lần.

+) Số 4 có mặt 2 lần, số 3 có mặt 1 lần, số 5 có mặt 0 lần, số 6 có mặt 1 lần.

TH3: Số 3 có mặt 0 lần, số 4 có mặt 2 lần, số 5 và 6 có mặt 1 lần $\Rightarrow$ Có $C_4^2.2! = 12$ số.

TH tương tự TH3:

Số 4 có mặt 0 lần, số 3 có mặt 2 lần, số 5 và 6 có mặt 1 lần.

TH4: Số 3 có mặt 1 lần, số 4 có mặt 1 lần, số 5 và 6 có mặt 1 lần $\Rightarrow$ Có $4! = 24$ số.

Vậy có $6 + 12.4 + 12.2 + 24 = 102$ số.

Chọn C.

Phương pháp giải:

Liệt kê và đếm số cách chọn $2$ bạn thỏa mãn có $1$ bạn nam và $1$ bạn nữ tổ khác.

Các trường hợp: nam tổ $I$ và nữ hai tổ còn lại; nam tổ $II$ và nữ hai tổ còn lại; nam tổ $III$ và nữ hai tổ còn lại

Lời giải chi tiết:

Số cách chọn $1$ bạn nam tổ $I$ và $1$ bạn nữ hai tổ còn lại là $C_3^1.C_9^1 = 27$ cách chọn.

Số cách chọn $1$ bạn nam tổ $II$ và $1$ bạn nữ hai tổ còn lại là $C_5^1.C_{11}^1 = 55$ cách chọn.

Số cách chọn $1$ bạn nam tổ $III$ và $1$ bạn nữ hai tổ còn lại là $C_6^1.C_{12}^1 = 72$ cách chọn.

Vậy có $27 + 55 + 72 = 154$ cách chọn.

Chọn A