30 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ thông hiểuLàm bàiQuảng cáo
Câu hỏi 1 : Tìm giá trị lớn nhất của hàm số \(y = 1 - 2\cos x - {\cos ^2}x\).
Đáp án: A Phương pháp giải: Lời giải chi tiết: Phương pháp: Tìm GTLN, GTNN của hàm số dạng \(y = f(g(x))\) + Đặt ẩn phụ \(t = g(x)\), tìm tập giá trị \(T\) của \(g(x)\) + Xét hàm số \(y = f(t)\) trên \(T\) + Từ đó suy ra GTLN , GTNN của hàm số đã cho. Cách giải Đặt \(t = \cos x\), ta có \(t \in [–1;1]\) Xét \(f\left( t \right) = 1-2t-{t^2}\) \(f'\left( t \right) = -2-2t < 0,\forall t \in \left( {-1;1} \right)\) \( \Rightarrow f\left( t \right) \leqslant f\left( {-1} \right) = 2,\forall t \in \left[ {-1;1} \right]\) Vậy GTLN của hàm số đã cho là \(2\) Chọn A Câu hỏi 2 : Gọi \(m,\,\,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = \dfrac{1}{2}x - \sqrt {x + 2} \) trên đoạn \(\left[ { - 1;34} \right]\). Tính tổng \(S = 3m + M\).
Đáp án: A Phương pháp giải: - Tính đạo hàm \(y'\) và tìm nghiệm của phương trình \(y' = 0\) thuộc \(\left[ { - 1;34} \right]\). - Tính giá trị của hàm số tại các điểm đầu mút và tại điểm là nghiệm của phương trình \(y' = 0\) thuộc \(\left[ { - 1;34} \right]\). - So sánh các giá trị này và kết luận GTNN, GTLN. Lời giải chi tiết: TXĐ : \(D = \left[ { - 2; + \infty } \right)\). Ta có : \(y' = \dfrac{1}{2} - \dfrac{1}{{2\sqrt {x + 2} }} = \dfrac{{\sqrt {x + 2} - 1}}{{2\sqrt {x + 2} }}\). Cho \(y' = 0 \Leftrightarrow \sqrt {x + 2} - 1 = 0\)\( \Leftrightarrow \sqrt {x + 2} = 1 \Leftrightarrow x = - 1 \in \left[ { - 1;34} \right]\). Lại có : \(y\left( { - 1} \right) = - \dfrac{3}{2},y\left( {34} \right) = 11\) nên \(m = \mathop {\min }\limits_{\left[ { - 1;34} \right]} y = y\left( { - 1} \right) = - \dfrac{3}{2};\,\,M = \mathop {\max }\limits_{\left[ { - 1;34} \right]} y = y\left( {34} \right) = 11\). Vậy \(3m + M = 3.\left( { - \dfrac{3}{2}} \right) + 11 = \dfrac{{13}}{2}\). Chọn A. Câu hỏi 3 : Giá trị lớn nhất của hàm số \(y = \dfrac{{{x^2} - 2x + 1}}{{x + 2}}\) trên đoạn\(\left[ {0;3} \right]\) bằng
Đáp án: D Phương pháp giải: Để tìm GTNN, GTLN của hàm số \(f\) trên đoạn \(\left[ {a;b} \right]\), ta làm như sau: - Tìm các điểm \({x_1};{x_2};...;{x_n}\) thuộc khoảng \(\left( {a;b} \right)\) mà tại đó hàm số \(f\) có đạo hàm bằng 0 hoặc không có đạo hàm. - Tính \(f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right);\,\,f\left( a \right);\,f\left( b \right)\) - So sánh các giá trị vừa tìm được. Số lớn nhất trong các giá trị đó chính là GTLN của \(f\) trên \(\left[ {a;b} \right]\); số nhỏ nhất trong các giá trị đó chính là GTNN của \(f\) trên \(\left[ {a;b} \right]\). Lời giải chi tiết: \(y = \dfrac{{{x^2} - 2x + 1}}{{x + 2}}\), \(x \in \left[ {0;3} \right]\) Ta có: \(y' = \dfrac{{\left( {2x - 2} \right)\left( {x + 2} \right) - \left( {{x^2} - 2x + 1} \right)}}{{{{\left( {x + 2} \right)}^2}}} = \dfrac{{{x^2} + 4x - 5}}{{{{\left( {x + 2} \right)}^2}}}\) \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left[ {0;3} \right]\\x = - 5 \notin \left[ {0;3} \right]\end{array} \right.\) Hàm số đã cho liên tục trên \(\left[ {0;3} \right]\), có: \(y\left( 0 \right) = \dfrac{1}{2},y\left( 1 \right) = 0,\,y\left( 3 \right) = \dfrac{4}{5}\,\,.\) Vậy \(\mathop {\max }\limits_{\left[ {0;3} \right]} y = y\left( 3 \right) = \dfrac{4}{5}\). Chọn D. Câu hỏi 4 : Tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^2} + \dfrac{2}{x}\) trên đoạn \(\left[ {\dfrac{1}{2};2} \right]\) bằng:
Đáp án: B Phương pháp giải: - Tính \(f'\left( x \right)\), giải phương trình \(f'\left( x \right) = 0\) và xác định các nghiệm \({x_i} \in \left[ {\dfrac{1}{2};2} \right]\). - Tính \(f\left( {\dfrac{1}{2}} \right),\,\,f\left( 2 \right),\,\,f\left( {{x_i}} \right)\). - Kết luận: \(\mathop {\max }\limits_{\left[ {\dfrac{1}{2};2} \right]} f\left( x \right) = \max \left\{ {f\left( {\dfrac{1}{2}} \right);\,\,f\left( 2 \right);\,\,f\left( {{x_i}} \right)} \right\}\), \(\mathop {\min }\limits_{\left[ {\dfrac{1}{2};2} \right]} f\left( x \right) = \min \left\{ {f\left( {\dfrac{1}{2}} \right);\,\,f\left( 2 \right);\,\,f\left( {{x_i}} \right)} \right\}\). Lời giải chi tiết: Hàm số đã cho xác định trên \(\left[ {\dfrac{1}{2};2} \right]\). Ta có \(y' = 2x - \dfrac{2}{{{x^2}}} = \dfrac{{2\left( {{x^3} - 1} \right)}}{{{x^2}}}\), \(y' = 0 \Leftrightarrow {x^3} - 1 = 0 \Leftrightarrow x = 1 \in \left[ {\dfrac{1}{2};2} \right]\). Ta có \(y\left( {\dfrac{1}{2}} \right) = \dfrac{{17}}{4};\,\,y\left( 2 \right) = 5,\,\,y\left( 1 \right) = 3\). Suy ra \(\mathop {\max }\limits_{\left[ {\dfrac{1}{2};2} \right]} y = y\left( 2 \right) = 5,\,\,\mathop {\min }\limits_{\left[ {\dfrac{1}{2};2} \right]} y = y\left( 1 \right) = 3\). Vậy \(\mathop {\max }\limits_{\left[ {\dfrac{1}{2};2} \right]} y.\mathop {\min }\limits_{\left[ {\dfrac{1}{2};2} \right]} y = 5.3 = 15\). Chọn B. Câu hỏi 5 : Giá trị lớn nhất của hàm số \(f\left( x \right) = - 2{x^4} + 4{x^2} + 10\) trên đoạn \(\left[ {0;\,\,2} \right]\) bằng:
Đáp án: C Phương pháp giải: Cách 1: +) Tìm GTLN và GTNN của hàm số \(y = f\left( x \right)\) trên \(\left[ {a;\;b} \right]\) bằng cách: +) Giải phương trình \(y' = 0\) tìm các nghiệm \({x_i}.\) +) Tính các giá trị \(f\left( a \right),\;f\left( b \right),\;\;f\left( {{x_i}} \right)\;\;\left( {{x_i} \in \left[ {a;\;b} \right]} \right).\) Khi đó: \(\mathop {\min }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \min \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\},\;\;\mathop {\max }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \max \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\}.\) Cách 2: Sử dụng chức năng MODE 7 để tìm GTLN, GTNN của hàm số trên \(\left[ {a;\;b} \right].\) Lời giải chi tiết: Xét hàm số \(f\left( x \right) = - 2{x^4} + 4{x^2} + 10\) trên \(\left[ {0;\,\,2} \right]\) ta có: \(f'\left( x \right) = - 8{x^3} + 8x\) \( \Rightarrow f'\left( x \right) = - 8{x^3} + 8x = 0\) \( \Leftrightarrow 8x\left( {{x^2} - 1} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = 1\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\, \in \left[ {0;\,\,2} \right]\\x = 1\,\, \in \left[ {0;\,\,2} \right]\\x = - 1\,\, \notin \left[ {0;\,\,2} \right]\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}f\left( 0 \right) = 10\\f\left( 1 \right) = 12\\f\left( 2 \right) = - 6\end{array} \right.\) \( \Rightarrow \mathop {Max}\limits_{\left[ {0;\,\,2} \right]} f\left( x \right) = f\left( 1 \right) = 12.\) Chọn C. Câu hỏi 6 : Giá trị nhỏ nhất của hàm số \(y = \dfrac{{x - 1}}{{x + 1}}\) trên đoạn \(\left[ {0;\,\,3} \right]\) bằng:
Đáp án: A Phương pháp giải: Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left[ {a;\,\,b} \right]\,\,\,\left( {a < b} \right)\) thì \(\mathop {Min}\limits_{\left[ {a;\,\,b} \right]} f\left( x \right) = f\left( a \right).\) Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left[ {a;\,\,b} \right]\,\,\,\left( {a < b} \right)\) thì \(\mathop {Min}\limits_{\left[ {a;\,\,b} \right]} f\left( x \right) = f\left( b \right).\) Lời giải chi tiết: Xét hàm số \(y = \dfrac{{x - 1}}{{x + 1}}\) trên đoạn \(\left[ {0;\,\,3} \right]\) ta có: \(y' = \dfrac{{1 + 1}}{{{{\left( {x + 1} \right)}^2}}} = \dfrac{2}{{{{\left( {x + 1} \right)}^2}}} > 0\,\,\forall x \in \left[ {0;\,\,3} \right]\) \( \Rightarrow \) Hàm số đã cho đồng biến trên \(\left[ {0;\,\,3} \right].\) \( \Rightarrow \mathop {Min}\limits_{\left[ {0;\,\,3} \right]} \dfrac{{x - 1}}{{x + 1}} = y\left( 0 \right) = - 1.\) Vậy \(\mathop {\min }\limits_{\left[ {0;\,\,3} \right]} y = - 1.\) Chọn A. Câu hỏi 7 : Xét các khẳng định sau: i. Nếu giá trị nhỏ nhất của hàm đa thức bậc bốn \(y = f\left( x \right)\) trên \(\mathbb{R}\) bằng \(m\) thì có số thực \({x_1}\) thỏa mãn \(f\left( {{x_1}} \right) = m,\,\,f\left( x \right) > m\,\,\forall x \in \left( { - \infty ; + \infty } \right)\backslash \left\{ {{x_1}} \right\}\). ii. Nếu giá trị nhỏ nhất của hàm đa thức bậc bốn \(y = f\left( x \right)\) trên \(\mathbb{R}\) bằng \(m\) thì có số thực \({x_1}\) thỏa mãn \(f\left( {{x_1}} \right) = m,\,\,f\left( x \right) \ge m\,\,\forall x \in \left( { - \infty ; + \infty } \right)\backslash \left\{ {{x_1}} \right\}\). iii. Nếu giá trị lớn nhất của hàm đa thức bậc bốn \(y = f\left( x \right)\) trên \(\mathbb{R}\) bằng \(M\) thì có số thực \({x_2}\) thỏa mãn \(f\left( {{x_2}} \right) = M,\,\,f\left( x \right) < M\,\,\forall x \in \left( { - \infty ; + \infty } \right)\backslash \left\{ {{x_2}} \right\}\). iv. Nếu giá trị lớn nhất của hàm đa thức bậc bốn \(y = f\left( x \right)\) trên \(\mathbb{R}\) bằng \(M\) thì có số thực \({x_2}\) thỏa mãn \(f\left( {{x_2}} \right) = M,\,\,f\left( x \right) \le M\,\,\forall x \in \left( { - \infty ; + \infty } \right)\backslash \left\{ {{x_2}} \right\}\). Số khẳng định đúng là:
Đáp án: D Phương pháp giải: Dựa vào khái niệm GTLN, GTNN của hàm số. Lời giải chi tiết: Có hai khẳng định đúng là: ii. Nếu giá trị nhỏ nhất của hàm đa thức bậc bốn \(y = f\left( x \right)\) trên \(\mathbb{R}\) bằng \(m\) thì có số thực \({x_1}\) thỏa mãn \(f\left( {{x_1}} \right) = m,\,\,f\left( x \right) \ge m\,\,\forall x \in \left( { - \infty ; + \infty } \right)\backslash \left\{ {{x_1}} \right\}\). iv. Nếu giá trị lớn nhất của hàm đa thức bậc bốn \(y = f\left( x \right)\) trên \(\mathbb{R}\) bằng \(M\) thì có số thực \({x_2}\) thỏa mãn \(f\left( {{x_2}} \right) = M,\,\,f\left( x \right) \le M\,\,\forall x \in \left( { - \infty ; + \infty } \right)\backslash \left\{ {{x_2}} \right\}\). Chọn D. Câu hỏi 8 : Gọi \(M,\,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \dfrac{{{x^2} + x + 3}}{{x - 2}}\) trên \(\left[ { - 2;\,\,1} \right].\) Giá trị của \(M + m\) bằng:
Đáp án: C Phương pháp giải: Cách 1: +) Tìm GTLN và GTNN của hàm số \(y = f\left( x \right)\) trên \(\left[ {a;\;b} \right]\) bằng cách: +) Giải phương trình \(y' = 0\) tìm các nghiệm \({x_i}.\) +) Tính các giá trị \(f\left( a \right),\;f\left( b \right),\;\;f\left( {{x_i}} \right)\;\;\left( {{x_i} \in \left[ {a;\;b} \right]} \right).\) Khi đó: \(\mathop {\min }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \min \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\},\;\;\mathop {\max }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \max \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\}.\) Cách 2: Sử dụng chức năng MODE 7 để tìm GTLN, GTNN của hàm số trên \(\left[ {a;\;b} \right].\) Lời giải chi tiết: Xét hàm số: \(y = \dfrac{{{x^2} + x + 3}}{{x - 2}}\) trên \(\left[ { - 2;\,\,1} \right]\) ta có: \(y' = \dfrac{{\left( {2x + 1} \right)\left( {x - 2} \right) - {x^2} - x - 3}}{{{{\left( {x - 2} \right)}^2}}}\) \( = \dfrac{{2{x^2} - 3x - 2 - {x^2} - x - 3}}{{{{\left( {x - 2} \right)}^2}}}\)\( = \dfrac{{{x^2} - 4x - 5}}{{{{\left( {x - 2} \right)}^2}}}\) \( \Rightarrow y' = 0 \Leftrightarrow {x^2} - 4x - 5 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = - 1 \in \left[ { - 2;\,\,1} \right]\\x = 5\,\, \notin \left[ { - 2;\,\,1} \right]\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}y\left( { - 2} \right) = - \dfrac{5}{4}\\y\left( { - 1} \right) = - 1\\y\left( 1 \right) = - 5\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}m = \mathop {Min}\limits_{\left[ { - 2;\,\,1} \right]} y = - 5\\M = \mathop {Max}\limits_{\left[ { - 2;\,\,1} \right]} y = - 1\end{array} \right.\) \( \Rightarrow M + m = - 1 - 5 = - 6.\) Chọn C. Câu hỏi 9 : Giá trị lớn nhất của hàm số \(f\left( x \right) = x + \sqrt {8 - {x^2}} \) bằng:
Đáp án: D Phương pháp giải: Cách 1: +) Tìm GTLN và GTNN của hàm số \(y = f\left( x \right)\) trên \(\left[ {a;\;b} \right]\) bằng cách: +) Giải phương trình \(y' = 0\) tìm các nghiệm \({x_i}.\) +) Tính các giá trị \(f\left( a \right),\;f\left( b \right),\;\;f\left( {{x_i}} \right)\;\;\left( {{x_i} \in \left[ {a;\;b} \right]} \right).\) Khi đó: \(\mathop {\min }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \min \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\},\;\;\mathop {\max }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \max \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\}.\) Cách 2: Sử dụng chức năng MODE 7 để tìm GTLN, GTNN của hàm số trên \(\left[ {a;\;b} \right].\) Lời giải chi tiết: Xét hàm số: \(f\left( x \right) = x + \sqrt {8 - {x^2}} \) ta có: TXĐ: \(D = \left[ { - 2\sqrt 2 ;\,\,2\sqrt 2 } \right]\) \(f'\left( x \right) = 1 - \dfrac{x}{{\sqrt {8 - {x^2}} }}\) \( \Rightarrow f'\left( x \right) = 0\)\( \Leftrightarrow 1 - \dfrac{x}{{\sqrt {8 - {x^2}} }} = 0\) \(\begin{array}{l} \Leftrightarrow \sqrt {8 - {x^2}} - x = 0 \Leftrightarrow \sqrt {8 - {x^2}} = x\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\8 - {x^2} = {x^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\2{x^2} = 8\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\\left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\end{array} \right.\\ \Leftrightarrow x = 2 \in \left[ { - 2\sqrt 2 ;\,\,2\sqrt 2 } \right]\\ \Rightarrow \left\{ \begin{array}{l}f\left( { - 2\sqrt 2 } \right) = - 2\sqrt 2 \\f\left( 2 \right) = 4\\f\left( {2\sqrt 2 } \right) = 2\sqrt 2 \end{array} \right.\\ \Rightarrow \mathop {Max}\limits_{\left[ { - 2\sqrt 2 ;\,\,\,2\sqrt 2 } \right]} f\left( x \right) = f\left( 2 \right) = 4.\end{array}\) Chọn D. Câu hỏi 10 : Tìm giá trị lớn nhất của hàm số \(y = f\left( x \right) = \sqrt {x - 1} + \sqrt {5 - x} \) trên đoạn \(\left[ {1;5} \right]\).
Đáp án: C Phương pháp giải: - Tìm TXĐ của hàm số. - Giải phương trình \(f'\left( x \right) = 0\), tìm các nghiệm \({x_i} \in \left[ {1;5} \right]\). - Tính các giá trị \(f\left( 1 \right),\,\,f\left( 5 \right),\,\,f\left( {{x_i}} \right)\). - Kết luận: \(\mathop {max}\limits_{\left[ {1;5} \right]} f\left( x \right) = \max \left\{ {f\left( 1 \right);f\left( 5 \right);f\left( {{x_i}} \right)} \right\}\). Lời giải chi tiết: TXĐ: \(\left\{ \begin{array}{l}x - 1 \ge 0\\5 - x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x \le 5\end{array} \right. \Rightarrow D = \left[ {1;5} \right]\). Ta có \(f'\left( x \right) = \dfrac{1}{{2\sqrt {x - 1} }} - \dfrac{1}{{2\sqrt {5 - x} }} = \dfrac{{\sqrt {5 - x} - \sqrt {x - 1} }}{{2\sqrt {x - 1} .\sqrt {5 - x} }}\). Cho \(f'\left( x \right) = 0 \Leftrightarrow \sqrt {5 - x} = \sqrt {x - 1} \) \( \Leftrightarrow 5 - x = x - 1\) \( \Leftrightarrow 2x = 6\) \( \Leftrightarrow x = 3 \in \left[ {1;5} \right]\). Mặt khác \(f\left( 1 \right) = 2,\,\,f\left( 3 \right) = 2\sqrt 2 ,\,\,f\left( 5 \right) = 2\). Vậy \(\mathop {max}\limits_{\left[ {1;5} \right]} f\left( x \right) = f\left( 3 \right) = 2\sqrt 2 \). Chọn C. Câu hỏi 11 : Gọi \(M,\,\,N\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right) = \left| {x - 3} \right|\sqrt {x + 1} \) trên đoạn \(\left[ {0;4} \right]\). Tính\(M + 2N\).
Đáp án: A Phương pháp giải: - Tìm TXĐ của hàm số. - Giải phương trình \(f'\left( x \right) = 0\), tìm các nghiệm \({x_i} \in \left[ {0;4} \right]\). - Tính các giá trị \(f\left( 0 \right),\,\,f\left( 4 \right),\,\,f\left( {{x_i}} \right)\). - Kết luận: \(\mathop {max}\limits_{\left[ {0;4} \right]} f\left( x \right) = \max \left\{ {f\left( 0 \right),\,\,f\left( 4 \right),\,\,f\left( {{x_i}} \right)} \right\},\,\,\mathop {min}\limits_{\left[ {0;4} \right]} f\left( x \right) = \min \left\{ {f\left( 0 \right),\,\,f\left( 4 \right),\,\,f\left( {{x_i}} \right)} \right\}\). Lời giải chi tiết: Hàm số xác định trên \(\left[ {0;4} \right]\). Ta có: \(f\left( x \right) = \left| {x - 3} \right|\sqrt {x + 1} = \sqrt {\left( {x + 1} \right){{\left( {x - 3} \right)}^2}} \). Xét hàm số \(g\left( x \right) = \left( {x + 1} \right){\left( {x - 3} \right)^2}\) trên đoạn \(\left[ {0;4} \right]\) ta có: \(\begin{array}{l}g'\left( x \right) = {\left( {x - 3} \right)^2} + \left( {x + 1} \right).2\left( {x - 3} \right)\\g'\left( x \right) = \left( {x - 3} \right)\left( {x - 3 + 2x + 2} \right)\\g'\left( x \right) = \left( {x - 3} \right)\left( {3x - 1} \right)\\g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3 \in \left[ {0;4} \right]\\x = \dfrac{1}{3} \in \left[ {0;4} \right]\end{array} \right.\end{array}\) Ta có: \(g\left( 0 \right) = 9,\,\,g\left( {\dfrac{1}{3}} \right) = \dfrac{{256}}{{27}},\,\,g\left( 3 \right) = 0,\,\,f\left( 4 \right) = 5\). Vậy \(\left\{ \begin{array}{l}M = \mathop {\max }\limits_{\left[ {0;4} \right]} f\left( x \right) = \sqrt {g\left( {\dfrac{1}{3}} \right)} = \dfrac{{16\sqrt 3 }}{9}\\N = \mathop {\min }\limits_{\left[ {0;4} \right]} f\left( x \right) = \sqrt {g\left( 0 \right)} = 0\end{array} \right.\)\( \Rightarrow M + 2N = \dfrac{{16\sqrt 3 }}{9}\). Chọn A. Câu hỏi 12 : Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \dfrac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) trên đoạn \(\left[ { - 4;0} \right]\) lần lượt là \(M\) và \(m\). Giá trị của tổng \(M + m\) bằng bao nhiêu?
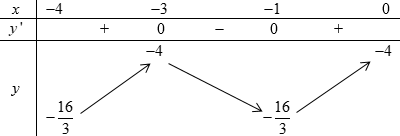
Đáp án: C Phương pháp giải: - Tìm đạo hàm của hàm số và tìm nghiệm \(y' = 0\). - Lập bảng biến thiên của hàm số trong khoảng yêu cầu. - Dựa vào bảng biến thiên để kết luận GTLN, GTNN của hàm số. Lời giải chi tiết: Hàm số \(y = \dfrac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) có TXĐ \(D = \mathbb{R}\). Ta có: \(y' = {x^2} + 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 3\end{array} \right.\) Bảng biến thiên trên đoạn \(\left[ { - 4;0} \right]\):
Dựa vào bảng biến thiên ta thấy trên đoạn \(\left[ { - 4;0} \right]\); hàm số có: Giá trị lớn nhất \(M = - 4\); giá trị nhỏ nhất \(m = - \dfrac{{16}}{3}\). Vậy \(M + m = - 4 - \dfrac{{16}}{3} = - \dfrac{{28}}{3}.\) Chọn C. Câu hỏi 13 : Kí hiệu \(m,\,\,M\) là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = \dfrac{{{x^2} + 3}}{{x + 1}}\) trên đoạn \(\left[ {0;2} \right]\). Giá trị của \(m + M\) bằng:
Đáp án: D Phương pháp giải: - Tính đạo hàm của hàm số, sử dụng công thức \(\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\). - Giải phương trình \(y' = 0\), xác định các nghiệm \({x_i} \in \left[ {0;2} \right]\). - Tính các giá trị \(y\left( 0 \right),\,\,y\left( 2 \right),\,\,y\left( {{x_i}} \right)\). - Kết luận: \(\mathop {\min }\limits_{\left[ {0;2} \right]} y = \min \left\{ {y\left( 0 \right),\,\,y\left( 2 \right),\,\,y\left( {{x_i}} \right)} \right\}\), \(\mathop {\max }\limits_{\left[ {0;2} \right]} y = \max \left\{ {y\left( 0 \right),\,\,y\left( 2 \right),\,\,y\left( {{x_i}} \right)} \right\}\). Lời giải chi tiết: ĐKXĐ: \(x + 1 \ne 0 \Leftrightarrow x \ne - 1\), do đó hàm số xác định trên \(\left[ {0;2} \right]\). \(\begin{array}{l}y' = \dfrac{{2x\left( {x + 1} \right) - \left( {{x^2} + 3} \right)}}{{{{\left( {x + 1} \right)}^2}}}\\y' = \dfrac{{{x^2} + 2x - 3}}{{{{\left( {x + 1} \right)}^2}}}\\y' = 0 \Leftrightarrow {x^2} + 2x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left[ {0;2} \right]\\x = - 3 \notin \left[ {0;2} \right]\end{array} \right.\end{array}\) Ta có: \(y\left( 0 \right) = 3,\,\,y\left( 2 \right) = \dfrac{7}{3},\,\,y\left( 1 \right) = 2\). \(\begin{array}{l} \Rightarrow m = \mathop {min}\limits_{\left[ {0;2} \right]} y = y\left( 1 \right) = 2\\\,\,\,\,\,M = \mathop {max}\limits_{\left[ {0;2} \right]} y = y\left( 0 \right) = 3\end{array}\) Vậy \(m + M = 2 + 3 = 5\). Chọn D. Câu hỏi 14 : Cho hàm số \(f\left( x \right) = {x^3} + \left( {{m^2} + 1} \right)x + {m^2} - 2\) với \(m\) là tham số thực. Tìm tất cả các giá trị của \(m\) để hàm số có giá trị nhỏ nhất trên đoạn \(\left[ {0;\,\,2} \right]\) bằng \(7.\)
Đáp án: D Phương pháp giải: Xét hàm số \(f\left( x \right) = {x^3} + \left( {{m^2} + 1} \right)x + {m^2} - 2\) trên \(\left[ {0;\,\,2} \right]\) ta có: \(f'\left( x \right) = 3{x^2} + {m^2} + 1 > 0\,\,\,\forall m\) \( \Rightarrow \) Hàm số đống biến trên \(\mathbb{R}\) \( \Rightarrow \mathop {Min}\limits_{\left[ {0;\,\,2} \right]} f\left( x \right) = f\left( 0 \right) = 7\) Lời giải chi tiết: Xét hàm số \(f\left( x \right) = {x^3} + \left( {{m^2} + 1} \right)x + {m^2} - 2\) trên \(\left[ {0;\,\,2} \right]\) ta có: \(f'\left( x \right) = 3{x^2} + {m^2} + 1 > 0\,\,\,\forall m\) \( \Rightarrow \) Hàm số đống biến trên \(\mathbb{R}.\) \(\begin{array}{l} \Rightarrow \mathop {Min}\limits_{\left[ {0;\,\,2} \right]} f\left( x \right) = f\left( 0 \right) = 7\\ \Leftrightarrow {m^2} - 2 = 7\\ \Leftrightarrow {m^2} = 9\\ \Leftrightarrow m = \pm 3.\end{array}\) Chọn D. Câu hỏi 15 : Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên bên dưới. Gọi \(M,\,\,m\) lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số \(y = f\left( x \right)\) khi \(x \in \left[ { - 3;3} \right]\). Giá trị \(M - 2m\) bằng:
Đáp án: B Phương pháp giải: Dựa vào BBT để tìm giá trị lớn nhất và nhỏ nhất của hàm số. Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left[ {a;\,\,b} \right]\,\,\,\left( {a < b} \right)\) thì \(\mathop {Min}\limits_{\left[ {a;\,\,b} \right]} f\left( x \right) = f\left( a \right).\) Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left[ {a;\,\,b} \right]\,\,\,\left( {a < b} \right)\) thì \(\mathop {Min}\limits_{\left[ {a;\,\,b} \right]} f\left( x \right) = f\left( b \right).\) Lời giải chi tiết: Dựa vào BBT ta thấy: \(\left\{ \begin{array}{l}\mathop {Max}\limits_{\left[ { - 3;\,\,3} \right]} f\left( x \right) = 4\,\,\,khi\,\,\,x = 3\\\mathop {Min}\limits_{\left[ { - 3;\,\,3} \right]} f\left( x \right) = - 3\,\,\,khi\,\,\,x = - 3\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}M = 4\\m = - 3\end{array} \right. \Rightarrow M - 2m = 4 - 2.\left( { - 3} \right) = 10.\) Chọn B. Câu hỏi 16 : Giá trị nhỏ nhất của hàm số \(y = \dfrac{1}{{x + 1}} + x\) trên nửa khoảng \(\left[ {0; + \infty } \right)\) bằng?
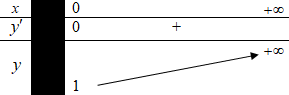
Đáp án: C Phương pháp giải: - Khảo sát hàm số trên nửa khoảng \(\left[ {0; + \infty } \right)\) và lập BBT của hàm số. - Dựa vào BBT xác định GTNN của hàm số. Lời giải chi tiết: Hàm số \(y = \dfrac{1}{{x + 1}} + x\)xác định trên nửa khoảng \(\left[ {0; + \infty } \right)\). Ta có : \(y' = - \dfrac{1}{{{{\left( {x + 1} \right)}^2}}} + 1 = \dfrac{{{{\left( {x + 1} \right)}^2} - 1}}{{{{\left( {x + 1} \right)}^2}}} \ge 0,\,\,\forall x \in \)\(\left[ {0; + \infty } \right)\) BBT:
Dựa vào BBT ta có: \(\mathop {\min }\limits_{\left[ {0; + \infty } \right)} y = y\left( 0 \right) = 1\). Chọn C. Câu hỏi 17 : Đợt xuất khẩu gạo của tỉnh A thường kéo dài trong 2 tháng (60 ngày). Người ta nhận thấy số lượng xuất khẩu gạo tính theo ngày thứ t được xác định bởi công thức \(S\left( t \right) = {t^3} - 72{t^2} + 405t + 3100\,\,\left( {1 \le t \le 60} \right)\). Hỏi trong mấy ngày đó thì ngày thứ mấy có số lượng xuất khẩu gạo cao nhất?
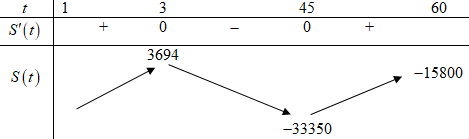
Đáp án: C Phương pháp giải: Sử dụng phương pháp hàm số để tìm GTLN của hàm số trên một đoạn. Lời giải chi tiết: Ta có: \(S'\left( t \right) = 3{t^2} - 144t + 405\), \(S'\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = 45\end{array} \right.\) BBT:
Như vậy, ngày thứ 3 có số lượng xuất khẩu gạo cao nhất. Chọn: C Câu hỏi 18 : Hàm số nào dưới đây có giá trị nhỏ nhất trên tập xác định?
Đáp án: C Phương pháp giải: Nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - \infty \) hoặc \(\mathop {\lim }\limits_{x \to - \infty } = - \infty \) hoặc \(\mathop {\lim }\limits_{x \to a} f\left( x \right) = - \infty \) thì hàm số \(y = f\left( x \right)\) không có giá trị nhỏ nhất trên tập xác định. Lời giải chi tiết: Các hàm số đã cho đều có TXĐ:\(D = \mathbb{R}\) Ta có: \(\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } \left( {{x^3} - 3x + 2} \right) = - \infty \\\mathop {\lim }\limits_{x \to + \infty } \left( { - 2{x^3} + 3{x^2} - 1} \right) = - \infty \\\mathop {\lim }\limits_{x \to \pm \infty } \left( {{x^4} - 2{x^2} - 1} \right) = + \infty \\\mathop {\lim }\limits_{x \to \pm \infty } \left( { - {x^4} + 4{x^2}} \right) = - \infty \end{array}\) Do đó, hàm số có giá trị nhỏ nhất trên tập xác định là \(y = {x^4} - 2{x^2} - 1\). Chọn C. Câu hỏi 19 : Gọi \(M\) và \(m\) là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 2{\sin ^2}x - \cos x + 1\). Khi đó, giá trị của tổng \(M + m\) bằng:
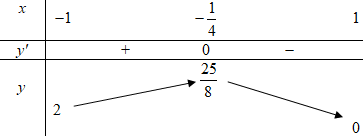
Đáp án: A Phương pháp giải: - Sử dụng công thức \({\sin ^2}x = 1 - {\cos ^2}x\). - Đặt ẩn phụ \(t = \cos x\), điều kiện \(t \in \left[ { - 1;1} \right]\). - Đưa hàm số về hàm số ẩn \(t\), tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { - 1;1} \right]\). - Giải phương trình \(y' = 0\), xác định các nghiệm \({x_i} \in \left[ { - 1;1} \right]\). - Tính các giá trị \(y\left( { - 1} \right),\,\,y\left( 1 \right),\,\,y\left( {{x_i}} \right)\). - Kết luận: \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = \min \left\{ {y\left( { - 1} \right);y\left( 1 \right);y\left( {{x_i}} \right)} \right\}\), \(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = \max \left\{ {y\left( { - 1} \right);y\left( 1 \right);y\left( {{x_i}} \right)} \right\}\). Lời giải chi tiết: \(\begin{array}{l}\,\,\,\,\,\,\,y = 2{\sin ^2}x - \cos x + 1\\ \Rightarrow y = 2\left( {1 - {{\cos }^2}x} \right) - \cos x + 1\\ \Rightarrow y = - 2{\cos ^2}x - \cos x + 3\end{array}\) Đặt \(\cos x = t\,\,\,\,\left( { - 1 \le t \le 1} \right)\), hàm số trở thành: \(y = - 2{t^2} - t + 3.\) Ta có: \(y' = - 4t - 1 = 0 \Rightarrow t = - \dfrac{1}{4}\,\,\,\left( {tm} \right)\). Bảng biến thiên:
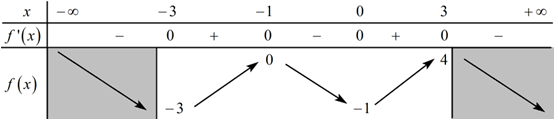
Từ BBT ta suy ra \(M = \dfrac{{25}}{8},\,\,m = 0\). Vậy \(M + m = \dfrac{{25}}{8}\). Chọn A. Câu hỏi 20 : Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên các khoảng \(\left( {\infty ;1} \right)\) và \(\left( {1; + \infty } \right)\). Đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ dưới. Mệnh đề nào sau đây là đúng?
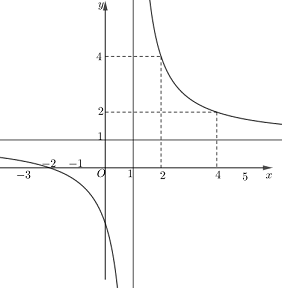
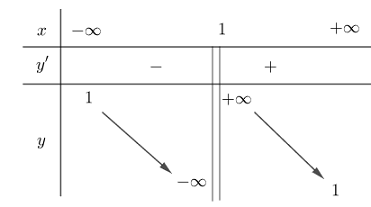
Đáp án: D Phương pháp giải: Lập BBT của hàm số từ đồ thị hàm số đã cho Từ BBT, tìm các giá trị lớn nhất, nhỏ nhất trên đoạn. Lời giải chi tiết: Từ đồ thị của hàm số đã cho ta có bảng biến thiên của hàm số như sau :
Từ BBT ta thấy hàm số đã cho nghịch biến trên từng khoảng xác định \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\). Suy ra \(\mathop {\min }\limits_{\left[ { - 3;0} \right]} f\left( x \right) = f\left( 0 \right);\,\,\mathop {\min }\limits_{\left[ {2;5} \right]} f\left( x \right) = f\left( 5 \right)\). Chọn D. Câu hỏi 21 : Tìm tất cả các giá trị thực của tham số \(m\) để giá trị lớn nhất của hàm số \(y = \dfrac{{x + {m^2}}}{{x - 1}}\) trên đoạn \(\left[ {2;3} \right]\) bằng \(11\).
Đáp án: C Phương pháp giải: Xét tính đồng biến, nghịch biến của hàm số trên \(\left[ {2;3} \right]\) để tìm giá trị lớn nhất của hàm số. Thay giá trị lớn nhất của hàm số để tìm \(m\). Lời giải chi tiết: TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\). Suy ra hàm số đã cho xác định là liên tục trên đoạn \(\left[ {2;3} \right]\). Ta có : \(\begin{array}{l}y = f\left( x \right) = \dfrac{{x + {m^2}}}{{x - 1}}\\ \Rightarrow f'\left( x \right) = \dfrac{{1\left( {x - 1} \right) - 1.\left( {x + {m^2}} \right)}}{{{{\left( {x - 1} \right)}^2}}} = \dfrac{{ - \left( {{m^2} + 1} \right)}}{{{{\left( {x - 1} \right)}^2}}} < 0,\forall x \in D\end{array}\) Suy ra hàm số đã cho nghịch biến trên từng khoảng xác định hay hàm số nghịch biến trên đoạn \(\left[ {2;3} \right]\). Do đó \(\mathop {\max }\limits_{\left[ {2;3} \right]} f\left( x \right) = f\left( 2 \right) \Leftrightarrow 11 = \dfrac{{2 + {m^2}}}{{2 - 1}} \Leftrightarrow {m^2} = 9 \Leftrightarrow m = \pm 3\). Chọn C. Câu hỏi 22 : Hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 1;3} \right]\) và có bảng biến thiên như sau
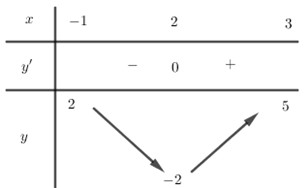
Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 1;3} \right]\) là
Đáp án: D Phương pháp giải: Dựa vào BBT để xác định giá trị nhỏ nhất của hàm số đã cho. Lời giải chi tiết: Từ BBT ta thấy GTNN của hàm số \(y = f\left( x \right)\) trên \(\left[ { - 1;3} \right]\) là \( - 2 \Leftrightarrow x = 2.\) Chọn D. Câu hỏi 23 : Nếu hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( x \right) < f\left( 0 \right)\,\,\,\forall x \in \left( { - 2;2} \right)\backslash \left\{ 0 \right\}\) thì:
Đáp án: B Phương pháp giải: Khái niệm cực trị của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên khoảng \(\left( {a;\,\,b} \right)\) và điểm \({x_0} \in \left( {a;\,\,b} \right).\) +) Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) < f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;\,\,{x_0} + h} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số \(f\left( x \right)\) đạt cực đại tại \({x_0}.\) +) Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) > f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;\,\,{x_0} + h} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số \(f\left( x \right)\) đạt cực tiểu tại \({x_0}.\) Lời giải chi tiết: Ta có: \(f\left( x \right) < f\left( 0 \right)\,\,\forall x \in \left( { - 2;\,\,2} \right)\backslash \left\{ 0 \right\} \Rightarrow x = 0\) là điểm cực đại của hàm số \(y = f\left( x \right).\) Chọn B. Câu hỏi 24 : Tính giá trị nhỏ nhất của hàm số \(y = \sqrt {4 - {x^2}} \) trên đoạn \(\left[ { - 1;1} \right].\)
Đáp án: A Phương pháp giải: Cách 1: +) Tìm GTLN và GTNN của hàm số \(y = f\left( x \right)\) trên \(\left[ {a;\;b} \right]\) bằng cách: +) Giải phương trình \(y' = 0\) tìm các nghiệm \({x_i}.\) +) Tính các giá trị \(f\left( a \right),\;f\left( b \right),\;\;f\left( {{x_i}} \right)\;\;\left( {{x_i} \in \left[ {a;\;b} \right]} \right).\) Khi đó: \(\mathop {\min }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \min \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\},\;\;\mathop {\max }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \max \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\}.\) Cách 2: Sử dụng chức năng MODE 7 để tìm GTLN, GTNN của hàm số trên \(\left[ {a;\;b} \right].\) Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left[ {a;\,\,b} \right]\,\,\,\left( {a < b} \right)\) thì \(\mathop {Min}\limits_{\left[ {a;\,\,b} \right]} f\left( x \right) = f\left( a \right).\) Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left[ {a;\,\,b} \right]\,\,\,\left( {a < b} \right)\) thì \(\mathop {Min}\limits_{\left[ {a;\,\,b} \right]} f\left( x \right) = f\left( b \right).\) Lời giải chi tiết: Xét hàm số \(y = \sqrt {4 - {x^2}} \) trên \(\left[ { - 1;\,\,1} \right].\) Ta có: \(y' = \dfrac{{ - 2x}}{{2\sqrt {4 - {x^2}} }} = \dfrac{{ - x}}{{\sqrt {4 - {x^2}} }}\) \(\begin{array}{l} \Rightarrow y' = 0 \Leftrightarrow x = 0 \in \left[ { - 1;\,\,1} \right]\\ \Rightarrow \left\{ \begin{array}{l}y\left( { - 1} \right) = \sqrt 3 \\y\left( 0 \right) = 4\\y\left( 1 \right) = \sqrt 3 \end{array} \right. \Rightarrow \mathop {Min}\limits_{\left[ { - 1;\,\,1} \right]} y = \sqrt 3 \,\,\,\,khi\,\,\,\,\left[ \begin{array}{l}x = - 1\\x = 1\end{array} \right..\end{array}\) Chọn A. Câu hỏi 25 : Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(f'\left( x \right) > 0\,\,\forall x \in \mathbb{R}.\) Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ {0;10} \right]\) bằng
Đáp án: A Phương pháp giải: Hàm số y = f (x) đồng biến trên [a; b] thì \(\mathop {Min}\limits_{\left[ {a;\,\,b} \right]} f\left( x \right) = f\left( a \right);\,\,\mathop {Max}\limits_{\left[ {a;\,\,b} \right]} f\left( x \right) = f\left( b \right).\) Lời giải chi tiết: Ta có: \(f'\left( x \right) > 0\,\,\forall x \in \mathbb{R} \Rightarrow \) hàm số đồng biến trên R. \( \Rightarrow \mathop {Max}\limits_{\left[ {0;\,\,10} \right]} f\left( x \right) = f\left( {10} \right).\) Đáp án A. Câu hỏi 26 : Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = - 3{x^2} - 2019.\) Với các số thực \(a,\,\,b\) thỏa mãn \(a < b,\) giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {a;\,\,b} \right]\) bằng:
Đáp án: C Phương pháp giải: Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left[ {a;\,\,b} \right]\,\,\,\left( {a < b} \right)\) thì \(\mathop {Min}\limits_{\left[ {a;\,\,b} \right]} f\left( x \right) = f\left( a \right).\) Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left[ {a;\,\,b} \right]\,\,\,\left( {a < b} \right)\) thì \(\mathop {Min}\limits_{\left[ {a;\,\,b} \right]} f\left( x \right) = f\left( b \right).\) Lời giải chi tiết: Ta có: \(f'\left( x \right) = - 3{x^2} - 2019 \le 0\,\,\,\forall x \Rightarrow \) hàm số \(y = f\left( x \right)\) nghịch biến trên tập xác định. \( \Rightarrow y = f\left( x \right)\) nghịch biến trên \(\left[ {a;\,\,b} \right] \Rightarrow \mathop {Min}\limits_{\left[ {a;\,\,b} \right]} f\left( x \right) = f\left( b \right).\) Chọn C. Câu hỏi 27 : Cho hàm số \(y = \dfrac{{x + 1}}{{x - {m^2}}}\)(\(m\) là tham số thực) thoả mãn \(\mathop {\min }\limits_{[ - 3; - 2]} = \dfrac{1}{2}\). Mệnh đề nào dưới đây đúng?
Đáp án: B Phương pháp giải: Lời giải chi tiết: Ta có: \(y' = \dfrac{{ - {m^2} - 1}}{{{{\left( {x - {m^2}} \right)}^2}}} = \dfrac{{ - \left( {{m^2} + 1} \right)}}{{{{\left( {x - {m^2}} \right)}^2}}} < 0\,\,\,\forall x \ne {m^2}\). Vì hàm số nghịch biến nên \(\mathop {\min }\limits_{\left[ { - 3; - 2} \right]} y = y\left( { - 2} \right) = \dfrac{1}{2}\). \( \Leftrightarrow \dfrac{{ - 2 + 1}}{{ - 2 - {m^2}}} = \dfrac{1}{2} \Leftrightarrow - 2 - {m^2} = - 2 \Leftrightarrow {m^2} = 0 \Leftrightarrow m = 0\). Chọn B Câu hỏi 28 : Một chất điểm chuyển động theo phương trình \(S\left( t \right) = - 2{t^3} + 18{t^2} + 2t + 1,\) trong đó \(t\) tính bằng giây \(\left( s \right)\) và \(S\left( t \right)\) tính bằng mét \(m\). Thời gian vận tốc chất điểm đạt giá trị lớn nhất là:
Đáp án: C Phương pháp giải: Lời giải chi tiết: + Ta có \(S\left( t \right) = - 2{t^3} + 18{t^2} + 2t + 1 \Rightarrow v\left( t \right) = S'\left( t \right) = - 6{t^2} + 36t + 2\). + \(v\left( t \right)\,\,\max \Leftrightarrow - 6{t^2} + 36t + 2\,\,\,\max \Leftrightarrow t = - \dfrac{b}{{2a}} = - \dfrac{{36}}{{2.\left( { - 6} \right)}} = 3\,\,\left( s \right)\). Chọn C Câu hỏi 29 : Hàm số \(y = \dfrac{{{x^3}}}{3} + \dfrac{{{x^2}}}{2} - 2x - 1\)đạt giá trị nhỏ nhấttrên [0;2] là:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Ta có \(y' = {x^2} + x - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\,\,\,\,\,\,\,\,\left( {tm} \right)\\x = - 2\,\,\,\left( {loai} \right)\end{array} \right.\). Ta có \(y\left( 1 \right) = - \dfrac{{13}}{6};\,\,\,y\left( 0 \right) = - 1;\,\,y\left( 2 \right) = - \dfrac{1}{3}\). \( \Rightarrow {y_{\min }} = y\left( 1 \right) = - \dfrac{{13}}{6}\). Chọn B Câu hỏi 30 : Giá trị lớn nhất của hàm số \(f\left( x \right) = {x^3} - 3x + 2\) trên đoạn \(\left[ { - 3;\,\,3} \right]\) bằng:
Đáp án: B Phương pháp giải: Cách 1: +) Tìm GTLN và GTNN của hàm số \(y = f\left( x \right)\) trên \(\left[ {a;\;b} \right]\) bằng cách: +) Giải phương trình \(y' = 0\) tìm các nghiệm \({x_i}.\) +) Tính các giá trị \(f\left( a \right),\;f\left( b \right),\;\;f\left( {{x_i}} \right)\;\;\left( {{x_i} \in \left[ {a;\;b} \right]} \right).\) Khi đó: \(\mathop {\min }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \min \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\},\;\;\mathop {\max }\limits_{\left[ {a;\;b} \right]} f\left( x \right) = \max \left\{ {f\left( a \right);\;f\left( b \right);\;f\left( {{x_i}} \right)} \right\}.\) Cách 2: Sử dụng chức năng MODE 7 để tìm GTLN, GTNN của hàm số trên \(\left[ {a;\;b} \right].\) Lời giải chi tiết: Ta có: \(f'\left( x \right) = 3{x^2} - 3\) \( \Rightarrow f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 3 = 0 \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right..\) Ta có: \(f\left( { - 3} \right) = - 16;\,\,\,f\left( { - 1} \right) = 4;\,\,f\left( 1 \right) = 0;\,\,\,f\left( 3 \right) = 20.\) \( \Rightarrow \mathop {\max }\limits_{\left[ { - 3;\,\,3} \right]} f\left( x \right) = f\left( 3 \right) = 20.\) Chọn B. Quảng cáo
|