30 bài tập trắc nghiệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số mức độ nhận biếtLàm bàiQuảng cáo
Câu hỏi 1 : Giá trị nhỏ nhất của hàm số \(y=2{{x}^{3}}+3{{x}^{2}}-12x+2\) trên đoạn \(\left[ -\,1;2 \right]\) đạt tại \(x={{x}_{0}}.\) Giá trị \({{x}_{0}}\) bằng bao nhiêu ?
Đáp án: B Phương pháp giải: Khảo sát hàm số trên đoạn để tìm giá trị nhỏ nhất – giá trị lớn nhất Lời giải chi tiết: Xét hàm số \(f\left( x \right)=2{{x}^{3}}+3{{x}^{2}}-12x+2\) trên \(\left[ -\,1;2 \right],\) có \({f}'\left( x \right)=6{{x}^{2}}+6x-12;\,\,\forall x\in \mathbb{R}.\) Phương trình \({f}'\left( x \right)=0\Leftrightarrow 6{{x}^{2}}+6x-12=0\Leftrightarrow \ \left[ \begin{align} & x=1\ \ \ \in \left[ -1;\ 2 \right] \\ & x=-2\ \ \notin \left[ -1;\ 2 \right] \\ \end{align} \right..\) Tính \(f\left( -\,1 \right)=15;\,\,f\left( 1 \right)=-\,5;\,\,f\left( 2 \right)=6.\) Do đó, hàm số đạt giá trị nhỏ nhất là \(-\,5.\) Xảy ra khi \(x=1.\) Chọn B Câu hỏi 2 : Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=2-\sin x.\) Khẳng định nào dưới đây là đúng?
Đáp án: D Phương pháp giải: Sử dụng tập giá trị của hàm \(y=\sin x:\ \ -1\le \operatorname{sinx}\le 1\) để đánh giá hàm số bài cho. Lời giải chi tiết: Ta có: \(-1\le \sin x\le 1\Rightarrow -1\le -\sin x\le 1\) \(\begin{align} \Rightarrow 2-1\le 2-\sin x\le 2+1\Leftrightarrow 1\le 2-\sin x\le 3. \\ \Rightarrow M=3;m=1. \\ \end{align}\) Chọn D. Câu hỏi 3 : Tìm giá trị nhỏ nhất của hàm số \(y=\frac{x-2}{x+1}\) trên đoạn \(\left[ 0;2 \right].\)
Đáp án: B Phương pháp giải: Hàm bậc nhất trên bậc nhất đơn điệu trên các khoảng xác định của nó. Lời giải chi tiết: TXĐ: \(D=R\backslash \left\{ -1 \right\}\) Ta có \(y'=\frac{3}{{{\left( x+1 \right)}^{2}}}>0\,\,\forall x\in \left[ 0;2 \right]\Rightarrow \) hàm số đồng biến trên [0;2] \(\Rightarrow \underset{\left[ 0;2 \right]}{\mathop{\min }}\,f\left( x \right)=f\left( 0 \right)=-2\) Chọn B. Câu hỏi 4 : Giá trị lớn nhất của \(y=-{{x}^{4}}+4{{x}^{2}}\) trên đoạn \(\left[ -1;2 \right]\) bằng:
Đáp án: B Phương pháp giải: Phương pháp tìm GTLN, GTNN của hàm số \(y=f\left( x \right)\) trên \(\left[ a;b \right]\). +) Giải phương trình \(y'=0\Rightarrow \) các nghiệm \({{x}_{i}}\in \left[ a;b \right]\). +) Tính các giá trị \(f\left( a \right);f\left( b \right);f\left( {{x}_{i}} \right)\). +) So sánh và kết luận: \(\underset{\left[ a;b \right]}{\mathop{\max }}\,f\left( x \right)=\max \left\{ f\left( a \right);f\left( b \right);f\left( {{x}_{i}} \right) \right\};\underset{\left[ a;b \right]}{\mathop{\min }}\,f\left( x \right)=\min \left\{ f\left( a \right);f\left( b \right);f\left( {{x}_{i}} \right) \right\}\) Lời giải chi tiết: TXĐ: \(D=R\). Ta có \(\begin{array}{l}y' = - 4{x^3} + 8x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \in \left[ { - 1;2} \right]\\x = \sqrt 2 \in \left[ { - 1;2} \right]\\x = - \sqrt 2 \notin \left[ { - 1;2} \right]\end{array} \right.\\y\left( 0 \right) = 0;y\left( {\sqrt 2 } \right) = 4;y\left( { - 1} \right) = 3;y\left( 2 \right) = 0 \Rightarrow \mathop {\max }\limits_{\left[ {a;b} \right]} y = 4\end{array}\) Chọn B. Câu hỏi 5 : Tìm GTNN của hàm số \(y={{x}^{4}}-{{x}^{2}}+13\) trên đoạn \(\left[ -2;3 \right]\).
Đáp án: A Phương pháp giải: Khảo sát sự biến thiên, đánh giá GTNN. Lời giải chi tiết: \(y={{x}^{4}}-{{x}^{2}}+13\Rightarrow y'=4{{x}^{3}}-2x\) \(\begin{array}{l}y' = 0 \Leftrightarrow 4{x^3} - 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \in \left[ { - 2;3} \right]\\x = \pm \frac{1}{{\sqrt 2 }} \in \left[ { - 2;3} \right]\end{array} \right.\\y\left( { - 1} \right) = 13;y\left( 3 \right) = 85;y\left( 0 \right) = 13;y\left( { \pm \frac{1}{{\sqrt 2 }}} \right) = \frac{{51}}{4}\end{array}\) Vậy, \(\underset{\left[ -1;3 \right]}{\mathop{Min}}\,y=y\left( \pm \frac{1}{\sqrt{2}} \right)=\frac{51}{4}\). Chọn: A Câu hỏi 6 : Giá trị nhỏ nhất của hàm số \(y={{x}^{3}}+3{{x}^{2}}-9x+1\) trên đoạn \(\left[ -\,4;4 \right]\) là
Đáp án: A Phương pháp giải: Cách 1 : Khảo sát hàm số, lập bảng biến thiên để tìm giá trị nhỏ nhất. Cách 2 : Giải phương trình \(y'=0\) tìm các nghiệm \({{x}_{i}}.\) +) Tính các giá trị \(y\left( {{x}_{i}} \right);\ \ y\left( a \right);\ \ y\left( b \right).\) +) So sánh các giá trị trên và kết luận giá trị nhỏ nhất của hàm số. Lời giải chi tiết:
Xét hàm số \(y={{x}^{3}}+3{{x}^{2}}-9x+1\) trên \(\left[ -\,4;4 \right],\) có \(y' = 0 \Leftrightarrow \left\{ \begin{array}{l} Tính giá trị \(y\left( -\,4 \right)=21;\,\,y\left( -\,3 \right)=28;\,\,y\left( 1 \right)=-\,4;\,\,y\left( 4 \right)=77.\) Vậy \(\underset{\left[ -\,4;4 \right]}{\mathop{\min }}\,y=-\,4.\) Chọn A Câu hỏi 7 : Cho hàm số \(y=f\left( x \right)\) có đạo hàm \({f}'\left( x \right)=-\,{{x}^{2}}-1.\) Với các số thực dương \(a,\,\,b\) thỏa mãn \(a<b.\) Giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ a;b \right]\) bằng
Đáp án: A Phương pháp giải: Hàm số đơn điệu trên đoạn nên giá trị nhỏ nhất – lớn nhất sẽ đạt tại đầu mút của đoạn Lời giải chi tiết: Ta có \({f}'\left( x \right)=-\,{{x}^{2}}-1<0;\,\,\forall x\in \left( a;b \right)\) suy ra \(f\left( x \right)\) là hàm số nghịch biến trên \(\left[ a;b \right].\) Mà \(a<b\)\(\Rightarrow \,\,f\left( a \right)>f\left( b \right).\) Vậy \(\underset{\left[ a;b \right]}{\mathop{\min }}\,f\left( x \right)=f\left( b \right).\) Chọn A Câu hỏi 8 : Giá trị nhỏ nhất của hàm số \(y=1+x+\frac{4}{x}\) trên đoạn \(\left[ -3;\,\,-1 \right]\) bằng
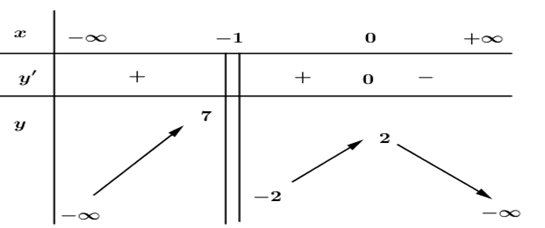
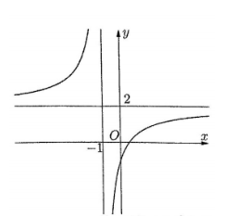
Đáp án: C Phương pháp giải: +) Giải phương trình \(y'=0\) để tìm các nghiệm \(x={{x}_{i}}.\) +) Ta tính các giá trị \(y\left( a \right);\ \ y\left( {{x}_{i}} \right);\ \ y\left( b \right)\) và kết luận giá trị nhỏ nhất của hàm số trên đoạn \(\left[ a;\ b \right].\) Lời giải chi tiết: Hàm số đã xác định và liên tục trên \(\left[ -3;-1 \right]\). Ta có : \(y'=1-\frac{4}{{{x}^{2}}}\Rightarrow y'=0\Leftrightarrow {{x}^{2}}=4\Leftrightarrow \left[ \begin{align} & x=-2\ \ \left( \in \left[ -3;\ -1 \right] \right) \\ & x=2\ \ \left( \notin \left[ -3;\ -1 \right] \right) \\ \end{align} \right..\) Tính \(y\left( -3 \right)=-\frac{10}{3}\text{; }y\left( -1 \right)=-4;\text{ }y\left( -2 \right)=-3\Rightarrow \underset{\left[ -3;-1 \right]}{\mathop{\min }}\,y=-4.\) Chọn C. Câu hỏi 9 : Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y={{x}^{3}}-3{{x}^{2}}-9x+35\) trên đoạn \(\left[ -\,4;4 \right].\) Giá trị của \(M\) và \(m\) lần lượt là
Đáp án: B Phương pháp giải: Khảo sát hàm số để tìm giá trị lớn nhất – giá trị nhỏ nhất trên đoạn. Lời giải chi tiết: Xét hàm số \(y={{x}^{3}}-3{{x}^{2}}-9x+35\) trên đoạn \(\left[ -\,4;4 \right],\) có \({y}'=3{{x}^{2}}-6x-9.\) Phương trình \(y' = 0 \Leftrightarrow \left\{ \begin{array}{l} Tính các giá trị \(f\left( -\,4 \right)=-\,41;\,\,f\left( -\,1 \right)=40;\,\,f\left( 3 \right)=8;\,\,f\left( 4 \right)=15.\) Vậy giá trị lớn nhất và nhỏ nhất của hàm số lần lượt là \(M=40;\,\,m=-\,41.\) Chọn B Câu hỏi 10 : Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau: Mệnh đền nào dưới đây sai?
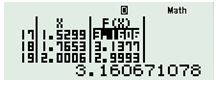
Đáp án: B Phương pháp giải: +) Dựa vào bảng biến thiên để đưa ra các nhận xét đúng. +) Hoành độ các điểm cực trị của hàm số là nghiệm của phương trình \(y'=0.\) Lời giải chi tiết: +) Ta có: \(\underset{x\to \pm \infty }{\mathop{\lim }}\,f\left( x \right)=-\infty \Rightarrow \) hàm số không có giá trị nhỏ nhất \(\Rightarrow \) A đúng. +) \(\underset{x\to -1}{\mathop{\lim }}\,f\left( x \right)=7\) và tại \(x=-1\) hàm số không xác định nên \(y=7\) không là giá trị lớn nhất của hàm số \(\Rightarrow \) B sai. +) Dựa vào đồ thị ta thấy hàm số đồng biến trên \(\left( -1;\,\,0 \right)\) và có 1 điểm cực đại \(\left( 0;2 \right)\). Chọn B. Câu hỏi 11 : Giá trị nhỏ nhất của hàm số \(y=2{{x}^{2}}-1\) trên đoạn \(\left[ -2;3 \right]\) là:
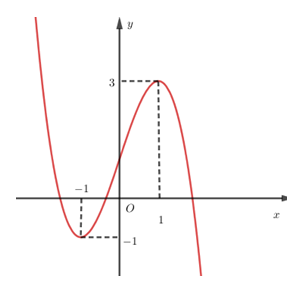
Đáp án: A Phương pháp giải: - Bước 1: Tính \(y'\), giải phương trình \(y'=0\) tìm các nghiệm \({{x}_{1}},{{x}_{2}},...{{x}_{n}}\) thỏa mãn \(a\le {{x}_{1}}<{{x}_{2}}<...<{{x}_{n}}\le b\). - Bước 2: Tính các giá trị \(f\left( a \right),f\left( {{x}_{1}} \right),...,f\left( {{x}_{n}} \right),f\left( b \right)\). - Bước 3: So sánh các giá trị tính được ở trên và kết luận: + Giá trị lớn nhất tìm được trong số các giá trị ở trên là GTLN \(M\) của hàm số trên \(\left[ a;b \right]\). + Giá trị nhỏ nhất tìm được trong số các giá trị ở trên là GTNN \(m\) của hàm số trên \(\left[ a;b \right]\). Lời giải chi tiết: Ta có: \(y'=4x=0\Leftrightarrow x=0\in \left[ -2;3 \right]\). \(y\left( 0 \right)=-1;y\left( -2 \right)=7;y\left( 3 \right)=17\). Do đó GTNN của \(y\) là \(-1\). Chọn A. Câu hỏi 12 : Giá trị lớn nhất của hàm số \(y=\sqrt{5-{{x}^{2}}}+x\) là:
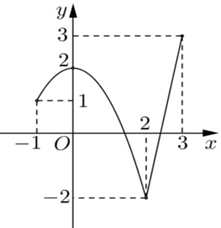
Đáp án: C Phương pháp giải: Tìm tập xác định của hàm số, sử dụng MTCT tìm GTLN của hàm số. Lời giải chi tiết: TXĐ : \(D=\left[ -\sqrt{5};\sqrt{5} \right]\) Sử dụng MTCT, ấn [MODE] [7], nhập hàm số \(y=\sqrt{5-{{x}^{2}}}+x\), \( Start=-\sqrt{5}\), \(End=\sqrt{5}\), \(Step=\frac{\sqrt{5}-\left( -\sqrt{5} \right)}{19}\) ta được : \(\Rightarrow \underset{\left[ -\sqrt{5};\sqrt{5} \right]}{\mathop{\max }}\,y\approx 3,16\approx \sqrt{10}\) Chọn C. Câu hỏi 13 : Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên, trong các khẳng định sau khẳng định nào là đúng?
Đáp án: D Phương pháp giải: Quan sát đồ thị và nhận xét.
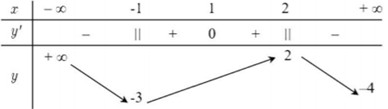
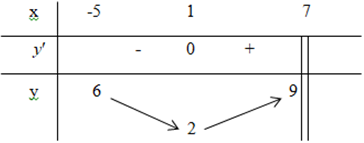
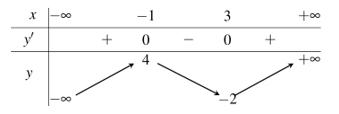
Lời giải chi tiết: Đáp án A sai vì hàm số bậc ba không có GTLN, GTNN trên \(R\). Đáp án B sai vì hàm số có giá trị cực đại \({y_{CD}} = 3\). Đáp án C sai vì hàm số đạt cực tiểu tại \({x_{CT}} = - 1\) và đạt cực đại tại \({x_{CD}} = 1\). Đáp án D đúng. Chọn D. Câu hỏi 14 : Cho hàm số liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có đồ thị như hình vẽ bên. Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 1;3} \right]\). Giá trị của \(M - m\) bằng:
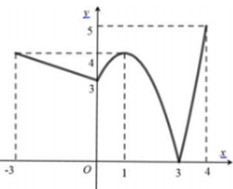
Đáp án: D Phương pháp giải: Lời giải chi tiết: Chọn D Câu hỏi 15 : Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 3;4} \right]\) và có đồ thị như hình vẽ bên. Gọi \(M\) và \(m\) lần lượt là các giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 3;4} \right]\). Tính \(M + m\).
Đáp án: A Phương pháp giải: GTLN, GTNN của hàm số \(y = f\left( x \right)\) trên \(\left[ { - 3;4} \right]\) lần lượt là giá trị của điểm cao nhất và điểm thấp nhất của đồ thị hàm số trên \(\left[ { - 3;4} \right]\). Lời giải chi tiết: Dựa vào đồ thị hàm số ta dễ dàng suy ra được \(M = \mathop {\max }\limits_{\left[ { - 3;4} \right]} f\left( x \right) = 5;\,\,m = \mathop {\min }\limits_{\left[ { - 3;4} \right]} f\left( x \right) = 0\). Vậy \(M + m = 5 + 0 = 5\). Chọn A. Câu hỏi 16 : Cho hàm số \(y = f\left( x \right)\) và có bảng biến thiên trên \({\rm{[}} - 5;7)\) như sau:
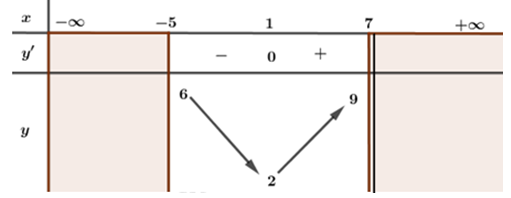
Mệnh đề nào sau đây đúng?
Đáp án: A Phương pháp giải: Dựa vào BBT để nhận xét các GTLN và GTNN của hàm số trên khoảng cần xét. Lời giải chi tiết: Dựa vào BBT ta thấy: \(\mathop {\min }\limits_{\left[ { - 5;\;7} \right)} f\left( x \right) = 2\;\;khi\;\;x = 1\) và hàm số không tồn tại GTLN trên \(\left[ { - 5;\;7} \right).\) Chọn A. Câu hỏi 17 : Tìm giá trị nhỏ nhất của hàm số \(y = \frac{{2x - 1}}{{ - x + 1}}\) trên đoạn \(\left[ {2;3} \right]\).
Đáp án: C Phương pháp giải: Hàm số bậc nhất trên bậc nhất đơn điệu trên từng khoảng xác định của nó. Lời giải chi tiết: TXĐ: \(D = R\backslash \left\{ 1 \right\}\). Ta có: \(y' = \frac{3}{{{{\left( { - x + 1} \right)}^2}}} > 0\,\,\forall x \in R\backslash \left\{ 1 \right\} \Rightarrow \) Hàm số đồng biến trên \(\left[ {2;3} \right]\). \( \Rightarrow \mathop {\min }\limits_{\left[ {2;3} \right]} y = y\left( 2 \right) = \frac{{2.2 + 1}}{{ - 2 + 1}} = - 5\). Chọn C. Câu hỏi 18 : Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây là mệnh đề đúng?
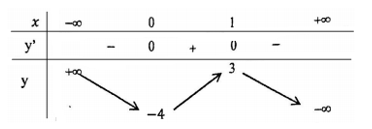
Đáp án: B Phương pháp giải: Dựa vào BBT của hàm số. Lời giải chi tiết:
Ta có \({y_{CD}} = 3\). Chọn đáp án B. Câu hỏi 19 : Cho bảng biến thiên của hàm số \(y = f\left( x \right)\) như sau: Gọi \(M = \mathop {\max }\limits_{\left[ { - 2;3} \right]} f\left( x \right)\) và \(m = \mathop {\min }\limits_{\left[ { - 2;3} \right]} f\left( x \right)\). Tìm giá trị của M và m?
Đáp án: C Phương pháp giải: Dựa vào BBT của đồ thị hàm số. Lời giải chi tiết:
\(\left\{ \begin{array}{l}M = \mathop {\max }\limits_{\left[ { - 2;3} \right]} f\left( x \right) = 2\\m = \mathop {\min }\limits_{\left[ { - 2;3} \right]} f\left( x \right) = - 1\end{array} \right.\) Chọn C. Câu hỏi 20 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R},\) có bảng biến thiên như hình sau:
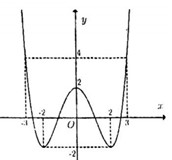
Trong các mệnh đề sau, mệnh đề nào sai?
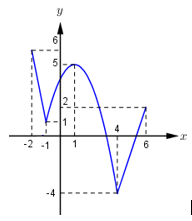
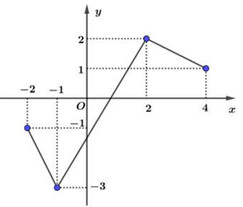
Đáp án: B Phương pháp giải: Lời giải chi tiết: Chọn B. Câu hỏi 21 : Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2;\,6} \right],\) có đồ thị hàm số như hình vẽ. Gọi \(M,\,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của \(f\left( x \right)\) trên miền \(\left[ { - 2;\,6} \right].\) Tính giá trị của biểu thức \(T = 2M + 3m.\)
Đáp án: B Phương pháp giải: Dựa vào đồ thị hàm số để kết luận giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Từ đó tính giá trị biểu thức cần tính. Lời giải chi tiết: Dựa vào đồ thị hàm số ta thấy hàm số có giá trị lớn nhất và giá trị nhỏ nhất trên \(\left[ { - 2;\,6} \right]\) lần lượt là: \(M = \mathop {\max }\limits_{\left[ { - 2;\,6} \right]} f\left( x \right) = 6;\,\,m = \mathop {\min }\limits_{\left[ { - 2;\,6} \right]} f\left( x \right) = - 4.\) \( \Rightarrow T = 2M + 3m = 2.6 + 3.\left( { - 4} \right) = 0.\) Chọn B. Câu hỏi 22 : Giá trị nhỏ nhất của hàm số \(y = {x^3} - 7{x^2} + 11x - 2\) trên đoạn \({\rm{[}}0;2]\) bằng
Đáp án: D Phương pháp giải: - Tính \(y'\), tìm các nghiệm của \(y' = 0\) nằm trong đoạn \(\left[ {0;2} \right]\). - Tính giá trị của hàm số tại các điểm trên (cả hai đầu mút) và so sánh. Lời giải chi tiết: Ta có: \(y' = 3{x^2} - 14x + 11 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left[ {0;2} \right]\\x = \dfrac{{11}}{3} \notin \left[ {0;2} \right]\end{array} \right.\). Lại có \(y\left( 0 \right) = - 2,y\left( 2 \right) = 0,y\left( 1 \right) = 3\) nên GTNN của hàm số là \( - 2\) đạt được tại \(x = 0\). Chọn D. Câu hỏi 23 : Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên trên \(\left[ { - 5;7} \right]\) như sau Mệnh đề bào dưới đây đúng?
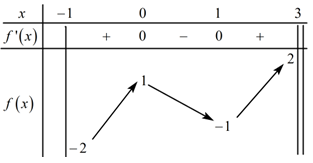
Đáp án: B Phương pháp giải: Dựa vào BBT, nhận xét các giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên khoảng xác định của nó. Lời giải chi tiết: Dựa vào BBT ta thấy: \(\mathop {\min }\limits_{\left[ { - 5;\,\,7} \right)} f\left( x \right) = 2\) khi \(x = 1,\) hàm số không đạt giá trị lớn nhất trên \(\left[ { - 5;\,7} \right).\) Chọn B. Câu hỏi 24 : Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 2;3} \right]\) bằng:
Đáp án: B Phương pháp giải: Dựa vào đồ thị hàm số, xác định điểm cao nhất của đồ thị hàm số trên \(\left[ { - 2;3} \right]\). Lời giải chi tiết: Giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 2;3} \right]\) bằng 4 đạt được khi \(x = 3\). Chọn: B Câu hỏi 25 : Cho hàm số \(y = f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình sau:
Mệnh đề nào sau đây đúng về hàm số \(y = f(x)\)?
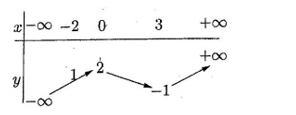
Đáp án: D Phương pháp giải: Dựa vào BBT nhận xét các đáp án và kết luận. Lời giải chi tiết: Dựa vào BBT ta thấy Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất trên \(\mathbb{R}.\) Chọn D. Câu hỏi 26 : Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên đoạn \(\left[ { - 2;2} \right]\) và có đồ thị là đường cong trong hình vẽ sau:
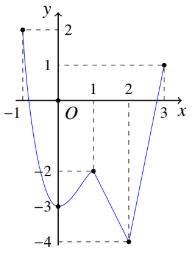
Đáp án: A Phương pháp giải: Dựa vào đồ thị hàm số để nhận xét giá trị nhỏ nhất của hàm số trên \(\left[ { - 2;2} \right].\) Lời giải chi tiết: Quan sát đồ thị hàm số, ta thấy: \(\mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = - 4\). Chọn: A Câu hỏi 27 : Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có đồ thị như hình vẽ. Gọi \(M,\,\,m\) lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn \(\left[ { - 1;3} \right]\). Giá trị của \(M + m\) là:
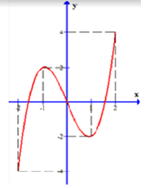
Đáp án: D Phương pháp giải: Dựa vào đồ thị hàm số, xác định GTLN, GTNN của hàm số trên đoạn \(\left[ { - 1;3} \right]\). Lời giải chi tiết: Trên đoạn \(\left[ { - 1;3} \right]\), ta có: \(\left\{ \begin{array}{l}M = \mathop {\max }\limits_{\left[ { - 1;3} \right]} y = y\left( { - 1} \right) = 2\\m = \mathop {\min }\limits_{\left[ { - 1;3} \right]} y = y\left( 2 \right) = - 4\end{array} \right. \Rightarrow M + m = 2 - 4 = - 2\).
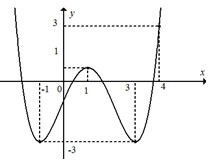
Chọn D Câu hỏi 28 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 1;4} \right]\) và có đồ thị như hình vẽ dưới đây.
Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên \(\left[ { - 1;4} \right]\). Giá trị của \(M + 2m\) bằng
Đáp án: B Phương pháp giải: Dựa vào đồ thị hàm số xác định điểm cao nhất (GTLN) và điểm thấp nhất (GTNN) của hàm số trên \(\left[ { - 1;4} \right]\). Lời giải chi tiết: Quan sát đồ thị hàm số ta thấy trên \(\left[ { - 1;4} \right] \Rightarrow \left\{ \begin{array}{l}M = \mathop {\max }\limits_{\left[ { - 1;4} \right]} f\left( x \right) = 3\\m = \mathop {\min }\limits_{\left[ { - 1;4} \right]} f\left( x \right) = - 3\end{array} \right. \Rightarrow M + 2m = 3 + 2.\left( { - 3} \right) = - 3\). Chọn B. Câu hỏi 29 : Cho hàm số \(y = f\left( x \right)\) có đồ thị trên đoạn \(\left[ { - 2;4} \right]\) như hình vẽ dưới . Giá trị \(\mathop {\min }\limits_{\left[ { - 2;4} \right]} f\left( x \right)\) bằng:
Đáp án: A Phương pháp giải: Dựa vào đồ thị hàm số xác định GTLN (điểm cao nhất) và GTNN (điểm thấp nhất) của đồ thị hàm số. Lời giải chi tiết: Dựa vào đồ thị hàm số ta thấy: \(\mathop {\min }\limits_{\left[ { - 2;4} \right]} f\left( x \right) = f\left( { - 1} \right) = - 3\). Chọn A. Câu hỏi 30 : Cho hàm số \(y = f\left( x \right)\) xác định trên nửa khoảng \(\left[ { - 1;\,\,3} \right)\) và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây đúng?
Đáp án: B Phương pháp giải: Dựa vào BBT để nhận xét GTLN và GTNN của hàm số. Lời giải chi tiết: Dựa vào BBT ta thấy: \(\mathop {\min }\limits_{\left[ { - 1;\,\,3} \right)} f\left( x \right) = - 2\) khi \(x = - 1.\) Chọn B. Quảng cáo
|