Đề thi tốt nghiệp THPT môn Lí

Đề tham khảo thi THPT môn Vật lí - Đề số 1 (hay, chi tiết)

Tải về

Làm đề thi

Nội năng của vật phụ thuộc vào

Đề bài

PHẦN I. CÂU TRẮC NGHIỆM PHƯƠNG ÁN NHIỀU LỰA CHỌN.

Câu 1 :

Nội năng của vật phụ thuộc vào

A

nhiệt độ và thể tích của vật.
B

khối lượng và nhiệt độ của vật.
C

khối lượng và thể tích của vật.
D

khối lượng của vật.

Câu 2 :

Nhiệt độ không tuyệt đối là nhiệt độ tại đó

A

nước đông đặc thành đá.
B

tất cả các chất khí hóa lỏng.
C

chuyển động nhiệt của phân tử hầu như dừng lại.
D

tất cả các chất khí hóa rắn.

Câu 3 :

Sự chuyển thể nào sau đây xảy ra tại nhiệt độ xác định?

A

Sự ngưng tụ.
B

Sự sôi.
C

Sự hóa hơi.
D

Sự bay hơi.

Câu 4 :

Tính chất không phải là của phân tử của vật chất ở thể khí là

A

chuyển động hỗn loạn.
B

chuyển động không ngừng.
C

chuyển động hỗn loạn và không ngừng.
D

chuyển động hỗn loạn xung quanh các vị trí cân bằng cố định.

Câu 5 :

Cần một áp suất rất lớn để nén một chất lỏng. Trong khi một chất khí được nén lại dễ dàng. Ý nào sau đây giải thích điều này?

A

Các phân tử chất lỏng ở gần nhau hơn và có lực tương tác phân tử mạnh hơn.
B

Các phân tử chất lỏng luôn chuyển động ngẫu nhiên.
C

Các phân tử chất khí ở xa nhau hơn và không tương tác với nhau.
D

Các phân tử chất khí thường xuyên va chạm với nhau và va chạm với thành bình chứa.

Câu 6 :

Trong quá trình đẳng áp của một lượng khí nhất định thì

A

thể tích tỉ lệ nghịch với nhiệt độ tuyệt đối
B

thể tích tỉ lệ nghịch với áp suất.
C

thể tích tỉ lệ thuận với nhiệt độ tuyệt đối.
D

thể tích tỉ lệ thuận với áp suất.

Câu 7 :

Quá trình đẳng nhiệt là quá trình biến đổi trạng thái của khối khí lí tưởng trong đó

A

nhiệt độ được giữ cố định.
B

áp suất được giữ cố định.
C

thể tích được giữ cố định.
D

khối lượng được thay đổi.

Câu 8 :

Các thông số nào sau đây xác định trạng thái của một khối lượng khí xác định?

A

Áp suất, thể tích, trọng lượng.
B

Áp suất, nhiệt độ, khối lượng.
C

Thể tích, khối lượng, nhiệt độ.
D

Áp suất, nhiệt độ, thể tích.

Câu 9 :

Với p là áp suất, V là thể tích, T là nhiệt độ tuyệt đối, m là khối lượng mol, m là khối lượng của khối khí, R là hằng số khí. Phương trình nào sau đây là phương trình Clayperon?

A

\(\frac{{pV}}{T} = R\).
B

\(\frac{{pV}}{T} = \mu R\).
C

\(\frac{{pV}}{R} = \frac{{mT}}{\mu }\).
D

\(\frac{{pV}}{T} = \frac{{\mu R}}{m}\).

Câu 10 :

Theo phương trình trạng thái của khí lí tưởng, tích của áp suất p và thể tích V của một khối lượng khí lí tưởng xác định

A

không phụ thuộc vào nhiệt độ.
B

tỉ lệ thuận với nhiệt độ tuyệt đối.
C

tỉ lệ thuận với nhiệt độ Xenxiut.
D

tỉ lệ nghịch với nhiệt độ tuyệt đối.

Câu 11 :

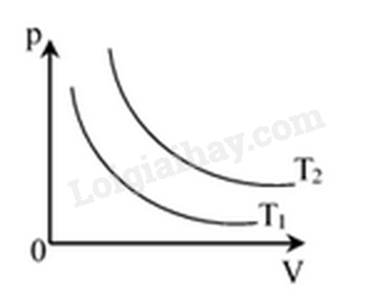
Đồ thị biểu diễn hai đường đẳng nhiệt của cùng một lượng khí lí tưởng biểu diễn như hình vẽ. Mối quan hệ về nhiệt độ của hai đường đẳng nhiệt này là

A

T₂ > T₁
B

T₂ = T₁
C

T₂ < T₁
D

T₂ ≤ T₁

Câu 12 :

Khi giãn nở khí đẳng nhiệt thì

A

áp suất khí tăng lên.
B

số phân tử khí trong một đơn vị thể tích tăng.
C

số phân tử khí trong một đơn vị thể tích giảm.
D

khối lượng riêng của khí tăng lên.

Câu 13 :

Các đường sức từ là các đường cong vẽ trong không gian có từ trường sao cho

A

pháp tuyến tại mọi điểm trùng với hướng của từ trường tại điểm đó.
B

tiếp tuyến tại mọi điểm trùng với hướng của từ trường tại điểm đó.
C

pháp tuyến tại mỗi điểm tạo với hướng của từ trường một góc không đổi.
D

tiếp tuyến tại mọi điểm tạo với hướng của từ trường một góc không đổi.

Câu 14 :

Trong hạt nhân nguyên tử \({}_{84}^{210}Po\) có

A

84 proton và 210 neutron.
B

126 proton và 84 neutron.
C

210 proton và 84 neutron.
D

84 proton và 126 neutron.

Câu 15 :

Đơn vị của cảm ứng từ là

A

T
B

N.A
C

kg.A
D

N/A

Câu 16 :

So sánh giữa hai phản ứng hạt nhân toả năng lượng phân hạch và nhiệt hạch. Chọn kết luận đúng:

A

Một phản ứng nhiệt hạch toả năng lượng nhiều hơn phản ứng phân hạch.
B

Cùng khối lượng, thì phản ứng nhiệt hạch toả năng lượng nhiều hơn phản ứng phân hạch.
C

Phản ứng phân hạch sạch hơn phản ứng nhiệt hạch.
D

Phản ứng nhiệt hạch có thể điều khiển được còn phản ứng phân hạch thì không.

Câu 17 :

Trong không khí thì tia nào chuyển động chậm nhất?

A

Tia γ.
B

Tia X.
C

Tia α.
D

Tia β.

Câu 18 :

Khi sét đánh, có dòng điện tích âm chuyển động từ đám mây xuống mặt đất. Từ trường của Trái Đất hướng về phía Bắc. Tia sét bị từ trường Trái Đất làm chệch hướng theo hướng nào?

A

Bắc.
B

Nam.
C

Đông
D

Tây.

PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI.

Câu 1 :

Một lượng nước và một lượng rượu có thể tích bằng nhau được cung cấp các nhiệt lượng tương ứng là Q₁ và Q₂. Biết khối lượng riêng của nước là 1000 kg/m³ và của rượu là 800 kg/m³, nhiệt dung riêng của nước là 4200 J/kg.K và của rượu là 2500 J/kg.K.

a) Nhiệt lượng để làm tăng nhiệt độ của 1 kg nước lên 1 K là 2500 J.

Đúng

Sai

b) Nhiệt lượng để làm tăng nhiệt độ của 1 kg rượu lên 1 K là 4200 J.

Đúng

Sai

c) Truyền cho 1 kg nước nhiệt lượng 42000 J thì nhiệt độ của nước tăng 10 °C.

Đúng

Sai

d) Để tăng nhiệt độ của lượng nước và lượng rượu nói trên lên 10⁰C thì Q₁=2,1Q₂.

Đúng

Sai

Câu 2 :

Một lượng khí xác định có thể tích V = 100 cm³, nhiệt độ 27 °C và áp suất 10⁵ Pa. Hằng số khí là R = 8,31 J/mol.K.

a) Nếu kết quả được làm tròn đến chữ số thứ ba sau dấu phẩy thập phân thì số mol của khối khí bằng 0,004 mol.

Đúng

Sai

b) Giữ nhiệt độ không đổi, tăng áp suất tới 1,25.10⁵ Pa thì thể tích khí khi đó bằng 80 cm³.

Đúng

Sai

c) Từ trạng thái ban đầu, nén khí để thể tích giảm đi 20 cm³, nhiệt độ khí tăng lên đến 39° thì áp suất khí lúc này bằng 5,2.10⁵ Pa

Đúng

Sai

d) Nếu thể tích giảm bằng \(\frac{1}{3}\) thể tích ban đầu và áp suất tăng 20% so với áp suất ban đầu thì nhiệt độ của khối khí sau khi nén bằng 120 °C.

Đúng

Sai

Câu 3 :

Một đoạn dây dẫn nằm ngang được giữ cố định ở vùng từ trường đều trong khoảng không gian giữa hai cực của nam châm. Nam châm này được đặt trên một cái cân như hình. Phần nằm trong từ trường của đoạn dây dẫn có chiều dài là 1,0 cm. Khi không có dòng điện chạy trong đoạn dây, số chỉ của cân là 500,68 g. Khi có dòng điện cường độ 0,34 A chạy trong đoạn dây, số chỉ của cân là 500,12 g. Lấy g = 9,80 m/s². Trong các phát biểu sau đây, phát biểu nào là đúng, phát biểu nào là sai?

a) Số chỉ của cân giảm đi chứng tỏ có một lực tác dụng vào cân theo chiều thẳng đứng lên trên.

Đúng

Sai

b) Lực tác dụng làm cho số chỉ của cân giảm là lực từ tác dụng lên đoạn dây và có chiều hướng lên.

Đúng

Sai

c) Lực từ tác dụng có thể làm thay đổi số chỉ trên cân ngay cả khi không có dòng điện chạy qua dây dẫn.

Đúng

Sai

d) Véc tơ cảm ứng từ \(\vec B\) có phương vuông góc với đoạn dây dẫn.

Đúng

Sai

Câu 4 :

Để điều trị ung thư tuyến giáp, một bệnh nhân đã nhân một liều lượng chất phóng xạ chứa 25mg \({}_{53}^{131}I\). Biết rằng \({}_{53}^{131}I\)là chất phóng xạ \({\beta ^ - }\)có chu kì bán rã là 8,02 ngày.

a) Phương trình phóng xạ của \({}_{53}^{131}I\)là \({}_{53}^{131}I \to {}_{54}^{131}Xe + {}_{ - 1}^0e + {}_0^0\tilde v\)

Đúng

Sai

b) Độ phóng xạ của liều thuốc tại thời điểm bệnh nhân sử dụng là 1,15.10¹⁴ Bq.

Đúng

Sai

c) Độ phóng xạ của liều thuốc sau khi sử dụng 7 ngày là 6,28.10¹³ Bq.

Đúng

Sai

d) Số hạt \({\beta ^ - }\)phát ra từ liều thuốc trong 7 ngày đó là \(5,{21.10^{20}}\)hạt.

Đúng

Sai

PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN.

Câu 1 :

Người ta thực hiện công 120 J để nén khí trong một xilanh. Tính độ biến thiên nội năng của khí theo đơn vị Jun, biết khí truyền ra môi trường xung quanh nhiệt lượng 80 J?

Đáp án:

Câu 2 :

Một miếng nhôm khối lượng 100 g ở nhiệt độ 20 °C. Biết Nhôm có nhiệt dung riêng là 896 J/kg.K, nhiệt nóng chảy riêng là 3,9.10⁵ J/kg. Nhiệt lượng cần cung cấp cho miếng Nhôm này để hoá lỏng ở nhiệt độ 658 °C là bao nhiêu kJ (Kết quả được làm tròn và lấy đến phần nguyên).

Đáp án:

Câu 3 :

Thể tích của một lượng khí xác định tăng thêm 10 % khi nhiệt độ của khí được tăng tới 47 °C. Xác định nhiệt độ ban đầu của lượng khí theo đơn vị Kelvin, biết quá trình trên là đẳng áp. (Kết quả được làm tròn đến phần nguyên)

Đáp án:

Câu 4 :

Một lò phản ứng phân hạch có công suất 200 MW. Cho rằng toàn bộ năng lượng mà lò phản ứng này sinh ra đều do sự phân hạch của ²³⁵U và đồng vị này chì bị tiêu hao bởi quá trình phân hạch. Coi mỗi năm có 365 ngày; mỗi phân hạch sinh ra 200 MeV; số Avôgađro N_A = 6,023.10²³ mol⁻¹. Khối lượng ²³⁵U mà lò phản ứng tiêu thụ trong 3 năm là bao nhiêu gam?

Đáp án:

Câu 5 :

Biết khối lượng của hạt nhân \(_{92}^{238}U\) là 238,00028 amu, khối lượng của proton và neutron là m_p=1.007276 amu; m_n = 1,008665 amu; 1 amu = 931 MeV/ c². Năng lượng liên kết của \(_{92}^{238}U\) là bao nhiêu? (Kết quả làm tròn đến phần nguyên)

Đáp án:

Câu 6 :

Một khung dây hình chữ nhật kín gồm N = 10 vòng dây, diện tích mỗi vòng s = 20 cm² đặt trong một từ trường đều có Vectơ cảm ứng từ hợp với pháp tuyến của mặt phang khung dây góc α = 60°, điện trở khung dây R = 0,2 Ω. Nếu trong thời gian Δt = 0,01 s, độ lớn cảm ứng từ giảm đều từ 0,04 T đến 0 thì cường độ dòng cảm ứng có độ lớn i₁; còn nếu độ lớn cảm ứng từ tăng đều từ 0 đến 0,02 T thì cường độ dòng cảm ứng có độ lớn i₂. Khi đó, i₁ + i₂ bằng bao nhiêu ampe?

Đáp án:

Lời giải và đáp án

PHẦN I. CÂU TRẮC NGHIỆM PHƯƠNG ÁN NHIỀU LỰA CHỌN.

Câu 1 :

Nội năng của vật phụ thuộc vào

A

nhiệt độ và thể tích của vật.
B

khối lượng và nhiệt độ của vật.
C

khối lượng và thể tích của vật.
D

khối lượng của vật.

Đáp án : A

Phương pháp giải :

Phân tích nội năng dựa vào khái niệm, xác định các yếu tố ảnh hưởng.

Lời giải chi tiết :

Nội năng của một vật là tổng động năng và thế năng của các phân tử cấu tạo nên vật. Nội năng phụ thuộc vào nhiệt độ (tức động năng của phân tử) và thể tích của vật (ảnh hưởng đến thế năng của phân tử do tương tác phân tử).

Đáp án: A

Câu 2 :

Nhiệt độ không tuyệt đối là nhiệt độ tại đó

A

nước đông đặc thành đá.
B

tất cả các chất khí hóa lỏng.
C

chuyển động nhiệt của phân tử hầu như dừng lại.
D

tất cả các chất khí hóa rắn.

Đáp án : C

Phương pháp giải :

Xem xét định nghĩa về nhiệt độ không tuyệt đối.

Lời giải chi tiết :

Nhiệt độ không tuyệt đối (0 K) là nhiệt độ mà tại đó chuyển động nhiệt của các phân tử gần như dừng lại hoàn toàn.

Đáp án: C

Câu 3 :

Sự chuyển thể nào sau đây xảy ra tại nhiệt độ xác định?

A

Sự ngưng tụ.
B

Sự sôi.
C

Sự hóa hơi.
D

Sự bay hơi.

Đáp án : B

Phương pháp giải :

Xem xét tính chất đặc trưng của các quá trình chuyển thể.

Lời giải chi tiết :

Trong các quá trình chuyển thể, chỉ có sự sôi xảy ra tại một nhiệt độ xác định (nhiệt độ sôi) đối với từng chất.

Đáp án: B

Câu 4 :

Tính chất không phải là của phân tử của vật chất ở thể khí là

A

chuyển động hỗn loạn.
B

chuyển động không ngừng.
C

chuyển động hỗn loạn và không ngừng.
D

chuyển động hỗn loạn xung quanh các vị trí cân bằng cố định.

Đáp án : D

Phương pháp giải :

Phân tích đặc điểm chuyển động của phân tử ở thể khí.

Lời giải chi tiết :

Phân tử ở thể khí chuyển động hỗn loạn và không ngừng. Chúng không chuyển động quanh các vị trí cân bằng cố định như ở thể rắn.

Đáp án: D

Câu 5 :

Cần một áp suất rất lớn để nén một chất lỏng. Trong khi một chất khí được nén lại dễ dàng. Ý nào sau đây giải thích điều này?

A

Các phân tử chất lỏng ở gần nhau hơn và có lực tương tác phân tử mạnh hơn.
B

Các phân tử chất lỏng luôn chuyển động ngẫu nhiên.
C

Các phân tử chất khí ở xa nhau hơn và không tương tác với nhau.
D

Các phân tử chất khí thường xuyên va chạm với nhau và va chạm với thành bình chứa.

Đáp án : A

Phương pháp giải :

So sánh đặc điểm cấu trúc phân tử của chất lỏng và chất khí.

Lời giải chi tiết :

Chất lỏng có các phân tử gần nhau hơn chất khí, tạo ra lực tương tác phân tử mạnh, khiến chất lỏng khó bị nén.

Đáp án: A

Câu 6 :

Trong quá trình đẳng áp của một lượng khí nhất định thì

A

thể tích tỉ lệ nghịch với nhiệt độ tuyệt đối
B

thể tích tỉ lệ nghịch với áp suất.
C

thể tích tỉ lệ thuận với nhiệt độ tuyệt đối.
D

thể tích tỉ lệ thuận với áp suất.

Đáp án : C

Phương pháp giải :

Dựa vào định luật Charles.

Lời giải chi tiết :

Sử dụng định luật Charles (quá trình đẳng áp): V~T thể tích tỉ lệ thuận với nhiệt độ tuyệt đối.

Đáp án: C

Câu 7 :

Quá trình đẳng nhiệt là quá trình biến đổi trạng thái của khối khí lí tưởng trong đó

A

nhiệt độ được giữ cố định.
B

áp suất được giữ cố định.
C

thể tích được giữ cố định.
D

khối lượng được thay đổi.

Đáp án : A

Phương pháp giải :

Dựa vào định nghĩa của quá trình đẳng nhiệt.

Lời giải chi tiết :

Quá trình đẳng nhiệt là quá trình giữ nhiệt độ không đổi, trong khi áp suất và thể tích thay đổi.

Đáp án: A

Câu 8 :

Các thông số nào sau đây xác định trạng thái của một khối lượng khí xác định?

A

Áp suất, thể tích, trọng lượng.
B

Áp suất, nhiệt độ, khối lượng.
C

Thể tích, khối lượng, nhiệt độ.
D

Áp suất, nhiệt độ, thể tích.

Đáp án : D

Phương pháp giải :

Liên hệ với phương trình trạng thái khí lý tưởng PV=nRT

Lời giải chi tiết :

Theo phương trình trạng thái khí lý tưởng PV=nRT, trạng thái của một khối khí xác định được xác định bởi áp suất, nhiệt độ và thể tích.

Đáp án: D

Câu 9 :

A

\(\frac{{pV}}{T} = R\).
B

\(\frac{{pV}}{T} = \mu R\).
C

\(\frac{{pV}}{R} = \frac{{mT}}{\mu }\).
D

\(\frac{{pV}}{T} = \frac{{\mu R}}{m}\).

Đáp án : C

Phương pháp giải :

Dạng cơ bản của phương trình Clausius-Clapeyron: \(pV = \frac{m}{\mu }RT\)

Lời giải chi tiết :

Phương trình trạng thái của khí lý tưởng là: \(pV = \frac{m}{\mu }RT\)

\(\begin{array}{l} \Rightarrow \frac{{pV}}{T} = \frac{m}{\mu }R\\ \Rightarrow \frac{{pV}}{R} = \frac{m}{\mu }T\end{array}\)

Đáp án: C

Câu 10 :

Theo phương trình trạng thái của khí lí tưởng, tích của áp suất p và thể tích V của một khối lượng khí lí tưởng xác định

A

không phụ thuộc vào nhiệt độ.
B

tỉ lệ thuận với nhiệt độ tuyệt đối.
C

tỉ lệ thuận với nhiệt độ Xenxiut.
D

tỉ lệ nghịch với nhiệt độ tuyệt đối.

Đáp án : B

Phương pháp giải :

Xác định mối quan hệ giữa pV và nhiệt độ từ phương trình trạng thái.

Lời giải chi tiết :

Từ phương trình trạng thái pV = nRT, tích pV tỉ lệ thuận với T

Đáp án: B

Câu 11 :

A

T₂ > T₁
B

T₂ = T₁
C

T₂ < T₁
D

T₂ ≤ T₁

Đáp án : A

Phương pháp giải :

So sánh vị trí của hai đường đẳng nhiệt.

Lời giải chi tiết :

Đường đẳng nhiệt có nhiệt độ cao hơn sẽ nằm phía trên vì áp suất cao hơn tại cùng một thể tích.

Đáp án: A

Câu 12 :

Khi giãn nở khí đẳng nhiệt thì

A

áp suất khí tăng lên.
B

số phân tử khí trong một đơn vị thể tích tăng.
C

số phân tử khí trong một đơn vị thể tích giảm.
D

khối lượng riêng của khí tăng lên.

Đáp án : C

Phương pháp giải :

Dựa vào định luật đẳng nhiệt khí lý tưởng (Boyle) và tính chất phân tử.

Lời giải chi tiết :

Quá trình đẳng nhiệt: pV = hằng số. Khi thể tích tăng, áp suất giảm và số phân tử trên một đơn vị thể tích giảm.

Đáp án: C

Câu 13 :

Các đường sức từ là các đường cong vẽ trong không gian có từ trường sao cho

A

pháp tuyến tại mọi điểm trùng với hướng của từ trường tại điểm đó.
B

tiếp tuyến tại mọi điểm trùng với hướng của từ trường tại điểm đó.
C

pháp tuyến tại mỗi điểm tạo với hướng của từ trường một góc không đổi.
D

tiếp tuyến tại mọi điểm tạo với hướng của từ trường một góc không đổi.

Đáp án : B

Phương pháp giải :

Phân tích định nghĩa đường sức từ.

Lời giải chi tiết :

Đường sức từ là đường mà tiếp tuyến tại mọi điểm của nó cho hướng của từ trường tại điểm đó.

Đáp án: B

Câu 14 :

Trong hạt nhân nguyên tử \({}_{84}^{210}Po\) có

A

84 proton và 210 neutron.
B

126 proton và 84 neutron.
C

210 proton và 84 neutron.
D

84 proton và 126 neutron.

Đáp án : D

Phương pháp giải :

Số proton bằng số hiệu nguyên tử, số neutron = số khối - số proton.

Lời giải chi tiết :

Z = 84, N = A – Z = 210 – 84 = 126

Vậy trong hạt nhân nguyên tử \({}_{84}^{210}Po\) có 84 proton và 126 neutron

Đáp án: D

Câu 15 :

Đơn vị của cảm ứng từ là

A

T
B

N.A
C

kg.A
D

N/A

Đáp án : A

Phương pháp giải :

Xác định đơn vị của cảm ứng từ từ công thức lực.

Lời giải chi tiết :

Đơn vị của cảm ứng từ là Tesla (T)

Đáp án: A

Câu 16 :

So sánh giữa hai phản ứng hạt nhân toả năng lượng phân hạch và nhiệt hạch. Chọn kết luận đúng:

A

Một phản ứng nhiệt hạch toả năng lượng nhiều hơn phản ứng phân hạch.
B

Cùng khối lượng, thì phản ứng nhiệt hạch toả năng lượng nhiều hơn phản ứng phân hạch.
C

Phản ứng phân hạch sạch hơn phản ứng nhiệt hạch.
D

Phản ứng nhiệt hạch có thể điều khiển được còn phản ứng phân hạch thì không.

Đáp án : B

Phương pháp giải :

Dựa vào đặc tính của hai loại phản ứng.

Lời giải chi tiết :

Phản ứng nhiệt hạch tạo ra năng lượng lớn hơn so với phân hạch trên cùng một khối lượng.

Đáp án: B

Câu 17 :

Trong không khí thì tia nào chuyển động chậm nhất?

A

Tia γ.
B

Tia X.
C

Tia α.
D

Tia β.

Đáp án : C

Phương pháp giải :

Dựa vào khối lượng và năng lượng của các tia.

Lời giải chi tiết :

Vận tốc của các loại tia: \({v_\alpha } < {v_\beta } < {v_{\rm{X}}} < {v_\gamma }\)

Đáp án: C

Câu 18 :

A

Bắc.
B

Nam.
C

Đông
D

Tây.

Đáp án : D

Phương pháp giải :

Áp dụng quy tắc bàn tay trái cho lực từ: \(\vec F = q(\vec v \times \vec B)\)

Lời giải chi tiết :

Với \(\vec v\) hướng xuống, \(\vec B\) hướng Bắc, lực từ sẽ hướng Tây.

Đáp án: D

PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI.

Câu 1 :

a) Nhiệt lượng để làm tăng nhiệt độ của 1 kg nước lên 1 K là 2500 J.

Đúng

Sai

b) Nhiệt lượng để làm tăng nhiệt độ của 1 kg rượu lên 1 K là 4200 J.

Đúng

Sai

c) Truyền cho 1 kg nước nhiệt lượng 42000 J thì nhiệt độ của nước tăng 10 °C.

Đúng

Sai

d) Để tăng nhiệt độ của lượng nước và lượng rượu nói trên lên 10⁰C thì Q₁=2,1Q₂.

Đúng

Sai

Đáp án

a) Nhiệt lượng để làm tăng nhiệt độ của 1 kg nước lên 1 K là 2500 J.

Đúng

Sai

b) Nhiệt lượng để làm tăng nhiệt độ của 1 kg rượu lên 1 K là 4200 J.

Đúng

Sai

c) Truyền cho 1 kg nước nhiệt lượng 42000 J thì nhiệt độ của nước tăng 10 °C.

Đúng

Sai

d) Để tăng nhiệt độ của lượng nước và lượng rượu nói trên lên 10⁰C thì Q₁=2,1Q₂.

Đúng

Sai

Phương pháp giải :

Sử dụng công thức tính nhiệt lượng: \(Q = mc{\rm{\Delta }}T\)

Lời giải chi tiết :

a) Nhiệt lượng để làm tăng nhiệt độ của 1 kg nước lên 1 K được tính bằng:

\(Q = mc{\rm{\Delta }}T = {c_1}.1.1 = 4200\;J\)

→Sai

b) Nhiệt lượng để làm tăng nhiệt độ của 1 kg rượu lên 1 K được tính bằng:

\(Q = mc{\rm{\Delta }}T = {c_2}.1.1 = 2500\;J\)

→Sai

c) Nhiệt lượng để làm tăng nhiệt độ của 1 kg nước lên 1 °C là \({c_1} = 4200{\rm{\;J/kg}}{\rm{.K}}\)

Truyền nhiệt lượng Q = 42000 J cho 1 kg nước: \({\rm{\Delta }}t = \frac{Q}{{mc}} = \frac{{42000}}{{1.4200}} = 10{\rm{\;^\circ C}}\)

→Đúng

d) Nhiệt lượng để làm tăng nhiệt độ của lượng nước lên ∆t = 10℃

Khối lượng của nước: \({m_1} = {\rho _1}V = 1000V\)

Nhiệt lượng: \({Q_1} = {m_1}{c_1}{\rm{\Delta }}t = (1000V).4200.10 = {42.10^6}.V{\rm{J}}\)

Nhiệt lượng để làm tăng nhiệt độ của lượng rượu lên ∆t = 10℃

Khối lượng của rượu: \({m_2} = {\rho _2}V = 800V\)

Nhiệt lượng: \({Q_2} = {m_2}{c_2}{\rm{\Delta }}t = (800V).2500.10 = {20.10^6}.V{\rm{J}}\)

\(\frac{{{Q_1}}}{{{Q_2}}} = \frac{{{{42.10}^6}}}{{{{20.10}^6}}} = 2,1\)

→Đúng

Câu 2 :

Một lượng khí xác định có thể tích V = 100 cm³, nhiệt độ 27 °C và áp suất 10⁵ Pa. Hằng số khí là R = 8,31 J/mol.K.

a) Nếu kết quả được làm tròn đến chữ số thứ ba sau dấu phẩy thập phân thì số mol của khối khí bằng 0,004 mol.

Đúng

Sai

b) Giữ nhiệt độ không đổi, tăng áp suất tới 1,25.10⁵ Pa thì thể tích khí khi đó bằng 80 cm³.

Đúng

Sai

c) Từ trạng thái ban đầu, nén khí để thể tích giảm đi 20 cm³, nhiệt độ khí tăng lên đến 39° thì áp suất khí lúc này bằng 5,2.10⁵ Pa

Đúng

Sai

d) Nếu thể tích giảm bằng \(\frac{1}{3}\) thể tích ban đầu và áp suất tăng 20% so với áp suất ban đầu thì nhiệt độ của khối khí sau khi nén bằng 120 °C.

Đúng

Sai

Đáp án

a) Nếu kết quả được làm tròn đến chữ số thứ ba sau dấu phẩy thập phân thì số mol của khối khí bằng 0,004 mol.

Đúng

Sai

b) Giữ nhiệt độ không đổi, tăng áp suất tới 1,25.10⁵ Pa thì thể tích khí khi đó bằng 80 cm³.

Đúng

Sai

c) Từ trạng thái ban đầu, nén khí để thể tích giảm đi 20 cm³, nhiệt độ khí tăng lên đến 39° thì áp suất khí lúc này bằng 5,2.10⁵ Pa

Đúng

Sai

d) Nếu thể tích giảm bằng \(\frac{1}{3}\) thể tích ban đầu và áp suất tăng 20% so với áp suất ban đầu thì nhiệt độ của khối khí sau khi nén bằng 120 °C.

Đúng

Sai

Phương pháp giải :

a) Sử dụng phương trình trạng thái khí lý tưởng: pV = nRT

b) Sử dụng định luật Boyle: pV = hằng số

c) Sử dụng phương trình trạng thái khí lý tưởng: pV = nRT

d) Sử dụng phương trình trạng thái khí lý tưởng: pV = nRT

Lời giải chi tiết :

a) Đúng.

Ta có: V = 100 cm³ = 10^-4 m³.

\(n = \frac{{PV}}{{RT}} = \frac{{{{10}^5}{{.10}^{ - 4}}}}{{8,31.300}} = 0,004{\rm{mol}}\)

b) Đúng.

Áp dụng định luật Boyle, ta có: \(PV = P'V' \Rightarrow V' = \frac{{PV}}{{P'}} = \frac{{{{10}^5}.100}}{{1,{{25.10}^5}}} = 80{\rm{c}}{{\rm{m}}^3}\)

c) Đúng.

Ta có: V’ = V – 20 = 100 – 20 = 80 cm³ = 8.10^-5 m³.

\(P' = \frac{{nRT'}}{{V'}} = \frac{{0,004.8,31.312}}{{{{8.10}^{ - 5}}}} = 5,{2.10^5}{\rm{Pa}}\)

d) Đúng.

Thể tích sau khi nén: \(V' = \frac{1}{3}.V = \frac{{100}}{3}{\rm{c}}{{\rm{m}}^3} = \frac{1}{3}{.10^{ - 4}}{{\rm{m}}^3}\)

Áp suất sau nén: \(P' = 1,2.P = 1,{2.10^5} = 1,{2.10^5}{\rm{Pa}}\)

Áp dụng phương trình trạng thái của khí lí tưởng, ta có:

\(T' = \frac{{P'V'}}{{nR}} = \frac{{1,{{2.10}^5}.\frac{{{{10}^{ - 4}}}}{3}}}{{0,004.8,31}} = 393{\rm{K}}\)

Nhiệt độ T’ = 393 K – 273 = 120 °C

Câu 3 :

a) Số chỉ của cân giảm đi chứng tỏ có một lực tác dụng vào cân theo chiều thẳng đứng lên trên.

Đúng

Sai

b) Lực tác dụng làm cho số chỉ của cân giảm là lực từ tác dụng lên đoạn dây và có chiều hướng lên.

Đúng

Sai

c) Lực từ tác dụng có thể làm thay đổi số chỉ trên cân ngay cả khi không có dòng điện chạy qua dây dẫn.

Đúng

Sai

d) Véc tơ cảm ứng từ \(\vec B\) có phương vuông góc với đoạn dây dẫn.

Đúng

Sai

Đáp án

a) Số chỉ của cân giảm đi chứng tỏ có một lực tác dụng vào cân theo chiều thẳng đứng lên trên.

Đúng

Sai

b) Lực tác dụng làm cho số chỉ của cân giảm là lực từ tác dụng lên đoạn dây và có chiều hướng lên.

Đúng

Sai

c) Lực từ tác dụng có thể làm thay đổi số chỉ trên cân ngay cả khi không có dòng điện chạy qua dây dẫn.

Đúng

Sai

d) Véc tơ cảm ứng từ \(\vec B\) có phương vuông góc với đoạn dây dẫn.

Đúng

Sai

Phương pháp giải :

Lực từ tác dụng lên dây dẫn: F = BIL

Sự thay đổi trọng lượng trên cân: \({\rm{\Delta }}F = {m_1}g - {m_2}g \Rightarrow F = {\rm{\Delta }}m.g\)

Lời giải chi tiết :

a) Đúng.

Trọng lượng thay đổi: \({\rm{\Delta }}m = {m_1} - {m_2} = 500,68 - 500,12 = 0,56\,{\rm{g}} = 0,00056\,{\rm{kg}}\)

Lực từ tác dụng: \(F = {\rm{\Delta }}m.g = 0,00056.9,8 = 0,005488\,{\rm{N}}\)

b) Đúng. Lực tác dụng làm giảm số chỉ cân là lực từ và có chiều hướng lên?

Phát biểu này đúng theo phân tích ở trên.

c) Sai. Không có dòng điện, lực từ F = BIL = 0

d) Đúng. Để tạo lực từ \(\vec F = \vec I \times \vec B\), \(\vec B\)phải vuông góc với dây dẫn.

Câu 4 :

a) Phương trình phóng xạ của \({}_{53}^{131}I\)là \({}_{53}^{131}I \to {}_{54}^{131}Xe + {}_{ - 1}^0e + {}_0^0\tilde v\)

Đúng

Sai

b) Độ phóng xạ của liều thuốc tại thời điểm bệnh nhân sử dụng là 1,15.10¹⁴ Bq.

Đúng

Sai

c) Độ phóng xạ của liều thuốc sau khi sử dụng 7 ngày là 6,28.10¹³ Bq.

Đúng

Sai

d) Số hạt \({\beta ^ - }\)phát ra từ liều thuốc trong 7 ngày đó là \(5,{21.10^{20}}\)hạt.

Đúng

Sai

Đáp án

a) Phương trình phóng xạ của \({}_{53}^{131}I\)là \({}_{53}^{131}I \to {}_{54}^{131}Xe + {}_{ - 1}^0e + {}_0^0\tilde v\)

Đúng

Sai

b) Độ phóng xạ của liều thuốc tại thời điểm bệnh nhân sử dụng là 1,15.10¹⁴ Bq.

Đúng

Sai

c) Độ phóng xạ của liều thuốc sau khi sử dụng 7 ngày là 6,28.10¹³ Bq.

Đúng

Sai

d) Số hạt \({\beta ^ - }\)phát ra từ liều thuốc trong 7 ngày đó là \(5,{21.10^{20}}\)hạt.

Đúng

Sai

Phương pháp giải :

Vận dụng kiến thức về phương trình phân rã \({\beta ^ - }\) của \({}_{53}^{131}I\)

Công thức tính độ phóng xạ: \(H = \lambda .N\)

Công thức tính lượng phóng xạ còn lại sau thời gian t: \({H_t} = {H_0}{.2^{\frac{{ - t}}{T}}}\)

Lời giải chi tiết :

a) Đúng. Phương trình phân rã đúng là: \({}_{53}^{131}I \to {}_{54}^{131}Xe + {}_{ - 1}^0e + {}_0^0\tilde v\)

b) Đúng.

\(\lambda = \frac{{\ln (2)}}{T} = \frac{{\ln (2)}}{{8,02.24.3600}} = 1,{00.10^{ - 6}}\,{{\rm{s}}^{ - 1}}\)

Số hạt ban đầu là: \(N = \frac{m}{M} \cdot {N_A} = \frac{{{{25.10}^{ - 3}}}}{{131}}.6,{022.10^{23}} = 1,{15.10^{20}}\)hạt

Độ phóng xạ: \(H = \lambda .N = 1,{00.10^{ - 6}}.1,{15.10^{20}} = 1,{15.10^{14}}{\rm{Bq}}\)

c) Đúng.

Độ phóng xạ còn lại sau 7 ngày là: \({H_t} = {H_0}{.2^{\frac{{ - t}}{T}}} \Rightarrow {H_t} = 1,{15.10^{14}}{.2^{ - \frac{7}{{8,02}}}} = 6,{28.10^{13}}{\rm{Bq}}\)

d) Đúng.

Số hạt phân rã trong 7 ngày: \({\rm{\Delta }}N = {N_0} - {N_t} \Rightarrow {\rm{\Delta }}N = {N_0}.\left( {1 - {2^{\frac{{ - t}}{T}}}} \right) \Rightarrow {\rm{\Delta }}N = 1,{15.10^{20}}.\left( {1 - {2^{ - \frac{7}{{8,02}}}}} \right) = 4,{87.10^{19}}\)

PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN.

Câu 1 :

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Áp dụng nguyên lý I của nhiệt động lực học: \({\rm{\Delta }}U = Q + A\)

Lời giải chi tiết :

Công thực hiện: A = 120 J

Nhiệt lượng truyền ra môi trường: Q = −80 J

Thay vào phương trình: \({\rm{\Delta }}U = Q + A = - 80 + 120 = 40\,{\rm{J}}\)

Đáp án: 40

Câu 2 :

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Nhiệt lượng cần cung cấp để làm nóng và làm tan chảy miếng nhôm bao gồm:

\(\begin{array}{l}Q = {Q_1} + {Q_2}\\{Q_1} = mc{\rm{\Delta }}T\\{Q_2} = m.\lambda \end{array}\)

Lời giải chi tiết :

\(\begin{array}{l}{Q_1} = mc{\rm{\Delta }}T \Rightarrow {Q_1} = 0,1.896.638 = 57228,8\,{\rm{J}}\\{Q_2} = m.\lambda \Rightarrow {Q_2} = 0,1.3,{9.10^5} = 39000\,{\rm{J}}\\ \Rightarrow Q = {Q_1} + {Q_2} = 57228,8 + 39000 = 96228,8\,{\rm{J}} \approx 96,2\,{\rm{kJ}}\end{array}\)

Đáp án: 96,2

Câu 3 :

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Áp dụng phương trình trạng thái của khí lý tưởng trong quá trình đẳng áp (Định luật Charles):

\(\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}} \Rightarrow {T_1} = \frac{{{T_2}.{V_1}}}{{{V_2}}}\)

Lời giải chi tiết :

\(\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}} \Rightarrow {T_1} = \frac{{{T_2}.{V_1}}}{{{V_2}}} \Rightarrow {T_1} = \frac{{320}}{{1,1}} = 290,9\,{\rm{K}} \approx 291\,{\rm{K}}\)

Đáp án: 291

Câu 4 :

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Công suất năng lượng sinh ra mỗi ngày: E = Pt => Tổng số phân hạch: N = E : E_{phân hạch} => Tính số hạt nhân ²³⁵U

Lời giải chi tiết :

Ta có: \(t = 3.365.24.3600 = 94608000\,{\rm{s}}\)

\(E = Pt = {200.10^6}.94608000 = 1,{892.10^{16}}\,{\rm{J}}\)

\(N = \frac{E}{{{E_{phanhach}}}} = \frac{{1,{{892.10}^{16}}}}{{200.1,{{6.10}^{ - 13}}}} = 5,{915.10^{28}}\)

\(N = \frac{m}{M}.{N_A} \Rightarrow m = \frac{{N.M}}{{{N_A}}} \Rightarrow m = \frac{{5,{{915.10}^{28}}.235}}{{6,{{023.10}^{23}}}} = 230,5\,{\rm{kg}} \approx 231\,{\rm{g}}\)

Đáp án: 231

Câu 5 :

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Năng lượng liên kết được tính từ độ hụt khối theo công thức: \({E_{{\rm{lk}}}} = {\rm{\Delta }}m.{c^2}\)

Lời giải chi tiết :

Độ hụt khối: \({\rm{\Delta }}m = Z.{m_p} + (A - Z).{m_n} - {m_U} \Rightarrow {\rm{\Delta }}m = 92.1,007276 + (238 - 92).1,008665 - 238,00028 = 0,928052amu\)

Năng lượng liên kết: \({E_{{\rm{lk}}}} = {\rm{\Delta }}m.{c^2} = 0,928052.931 = 864,0\,{\rm{MeV}}\)

Đáp án: 864

Câu 6 :

Đáp án:

Đáp án

Đáp án:

Phương pháp giải :

Áp dụng định luật Faraday về cảm ứng điện từ
Suất điện động cảm ứng trong khung dây: \(\mathcal{E} = - N.\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}\)

Dòng điện cảm ứng: \(i = \frac{\mathcal{E}}{R}\)

Lời giải chi tiết :

Trường hợp 1: Độ lớn cảm ứng từ giảm từ 0,04 T xuống 0

\(\begin{array}{l}{\rm{\Delta }}{B_1} = 0 - 0,04 = - 0,04\,{\rm{T}}\\{\rm{\Delta }}{{\rm{\Phi }}_1} = {\rm{\Delta }}{B_1}.s.\cos \alpha = - 0,{04.20.10^{ - 4}}.\frac{1}{2} = - {4.10^{ - 4}}\,{\rm{Wb}}\\{\mathcal{E}_1} = - N.\frac{{{\rm{\Delta }}{{\rm{\Phi }}_1}}}{{{\rm{\Delta }}t}} = - 10.\frac{{ - {{4.10}^{ - 4}}}}{{0,01}} = 0,4\,{\rm{V}}\\ \to {i_1} = \frac{{{\mathcal{E}_1}}}{R} = \frac{{0,4}}{{0,2}} = 2\,{\rm{A}}\end{array}\)

Trường hợp 2: Độ lớn cảm ứng từ tăng từ 0 lên 0,02 T

\(\begin{array}{l}{\rm{\Delta }}{B_2} = 0,02 - 0 = 0,02\,{\rm{T}}\\{\rm{\Delta }}{{\rm{\Phi }}_2} = {\rm{\Delta }}{B_2}.s.\cos \alpha = 0,{02.20.10^{ - 4}}.\frac{1}{2} = {2.10^{ - 4}}\,{\rm{Wb}}\\{\mathcal{E}_2} = - N.\frac{{{\rm{\Delta }}{{\rm{\Phi }}_2}}}{{{\rm{\Delta }}t}} = - 10.\frac{{{{2.10}^{ - 4}}}}{{0,01}} = - 0,2\,{\rm{V}}\\ \to {i_2} = \frac{{{\mathcal{E}_2}}}{R} = \frac{{0,2}}{{0,2}} = 1\,{\rm{A}}\end{array}\)

Tổng dòng cảm ứng: \({i_1} + {i_2} = 2 + 1 = 3\,{\rm{A}}\)

Đáp án: 3

Bài liên quan