Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương 1 - Hình học 7

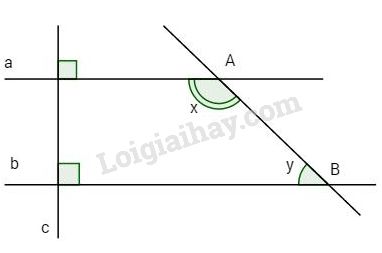
Đề bài

Bài 1.Cho hình vẽ, biết \(a \bot c,\,\,b \bot c\) và \({x \over y} = {3 \over 2}\). Tìm số đo góc x và y.

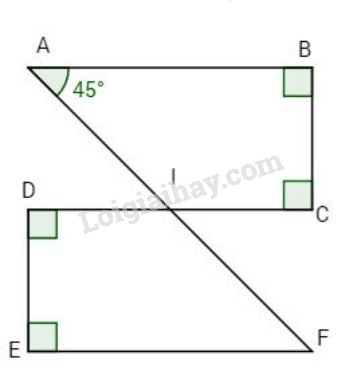
Bài 2. Cho hình vẽ.

a) Tính \(\widehat {AIC}\).

b) Chứng minh AB // EF.

c) Tính \(\widehat {IFE}\).

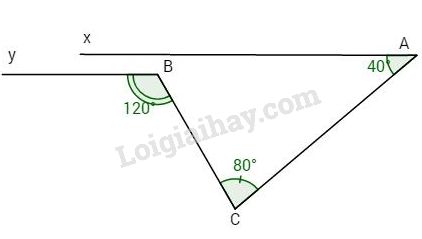
Bài 3. Cho hình vẽ, biết \(\widehat {yBC} = {120^o};\,\,\widehat {BCA} = {80^o};\)\(\,\widehat {xAC} = {40^o}.\)

Chứng minh Ax // By.

Phương pháp giải:

+\(\left\{ \matrix{ a \bot c \hfill \cr b \bot c \hfill \cr}  \right. \Rightarrow a//b\)

+\(\left\{ {\begin{array}{*{20}{c}}{a//b}\\{b//c}\end{array}} \right. \Rightarrow a//c\)

+Nếu một đường thẳng cắt hai đường thẳng trong các cặp góc tạo thành có 1 cặp góc so le trong bằng nhau thì chúng hai đường thẳng đó song song với nhau

+Tính chất dãy tỉ số bằng nhau

LG bài 1

Lời giải chi tiết:

Bài 1. Ta có \(a \bot c\) (giả thiết)

\(b \bot c\) (giả thiết)

\( \Rightarrow a//b \Rightarrow x + y = {180^o}\) (cặp góc trong cùng phía)

Lại có \(\dfrac{x}{y} = \dfrac{3}{2} \)

\(\Rightarrow \dfrac{x}{3} = \dfrac{y}{2} = \dfrac{{x + y}}{{3 + 2}} = \dfrac{{{{180}^o}}}{5} = {36^o}\)

\( \Rightarrow \dfrac{x}{ 3} = {36^o} \Rightarrow x = {108^o}\) và \(y = {72^o}.\)

LG bài 2

Lời giải chi tiết:

Bài 2.a) Ta có \(AB \bot BC\) (giả thiết)

\(IC \bot BC\) (giả thiết)

\( \Rightarrow AB//IC\,(1)\, \Rightarrow \widehat A + \widehat {AIC} + {180^o}\) (trong cùng phía)

\(\, \Rightarrow {45^o} + \widehat {AIC} + {180^o}\)

\(\Rightarrow \widehat {AIC} = {180^o} - {45^o} = {135^o}.\)

Vậy \({\widehat {AIC}^o} = {135^o}\).

b) Ta có \(\left. \matrix{ IC \bot DE \hfill \cr DE \bot {\rm{EF}} \hfill \cr}  \right\} \)

\(\Rightarrow IC//EF\,(2).\)

Từ (1) và (2) \( \Rightarrow AB//EF\) (hai đường thẳng phân biệt cùng vuông góc với đường thứ ba thì chúng song song).

c) Ta có \(\widehat {DIF} = \widehat {AIC} = {135^o}\) (đối đỉnh), mà \(\widehat {DIF}\) và \(\widehat {IEF}\) là hai góc trong cùng phía, lại có IC // EF (chứng minh trên)

\(\widehat {DIF} + \widehat {IEF} = {180^o} \)

\(\Rightarrow {135^o} + \widehat {IEF} = {180^o}\)

\(\Rightarrow \widehat {IEF} = {180^o} - {135^o} = {45^o}.\)

LG bài 3

Lời giải chi tiết:

Bài 3. Kẻ tia Ct so cho CA nằm trong góc \(\widehat {BCt}\)và Ct//By khi đó \(\widehat B\) và \(\widehat {BCt}\) là hai góc so le trong \(\widehat B = \widehat {BCt} = {120^o}\).

Vì tia CA nằm giữa hai tia CB và Ct nên \(\widehat {BAC} + \widehat {ACt} = \widehat {BCt} \)

\(\Rightarrow {80^o} + \widehat {ACt} = {120^o} \)

\(\Rightarrow \widehat {ACt} = {120^o} - {80^o} = {40^o}.\)

Ta có \(\widehat {ACt}\) và \(\widehat A\) là hai góc so le trong, mà \(\widehat {ACt} = \widehat A = {140^o} \Rightarrow \) Ct//Ax.

Lại có Ct // By (cách vẽ) \( \Rightarrow \) Ax // By (hai đường thẳng phân biệt cùng song song với đường thứ ba thì chúng song song).

Loigiaihay.com