Đề kiểm tra 45 phút ( 1 tiết) - Đề số 2 - Chương 1 - Đại số 8Giải Đề kiểm tra 45 phút ( 1 tiết) - Đề số 2 - Chương 1 - Đại số 8 Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài Bài 1. Rút gọn biểu thức: a) \(A = \left( {2x + 3} \right)\left( {4{x^2} - 6x + 9} \right) \)\(- 2\left( {4{x^3} - 1} \right).\) b) \(B = {\left( {x - 1} \right)^3} - 4x\left( {x + 1} \right)\left( {x - 1} \right)\)\( + 3\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)\). Bài 2. Phân tích các đa thức sau thành nhân tử: a) \({x^2} - {y^2} - 3x + 3y\) b) \({\left( {b - a} \right)^2} + \left( {a - b} \right)\left( {3a - 2b} \right)\)\( - {a^2} + {b^2}.\) Bài 3. Tìm x, biết: \({\left( {2x - 1} \right)^2} - {\left( {3x + 4} \right)^2} = 0.\) Bài 4. Tìm m để đa thức \(A\left( x \right) = {x^4} - {x^3} + 6{x^2} - x + m\) chia cho đa thức \(B(x) = {x^2} - x + 5\) có số dư bằng 2. Bài 5. Tìm giá trị lớn nhất của biểu thức: \(P(x) = - {x^2} + 2x + 5.\) LG bài 1 Phương pháp giải: Sử dụng qui tắc nhân đơn thức với đa thức, đa thức với đa thức và các hằng đẳng thức: \(\begin{array}{l} Lời giải chi tiết: a) \(A = \left( {2x + 3} \right)\left( {4{x^2} - 6x + 9} \right) \)\(- 2\left( {4{x^3} - 1} \right)\) \(=\left( {8{x^3} + 27} \right) - 2\left( {4{x^3} - 1} \right) \) \(= 8{x^3} + 27 - 8{x^3} + 2 = 29.\) b) \(B = {\left( {x - 1} \right)^3} - 4x\left( {x + 1} \right)\left( {x - 1} \right)\)\( + 3\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)\). \(= {x^3} - 3{x^2} + 3x - 1 - 4x\left( {{x^2} - 1} \right) + 3\left( {{x^3} - 1} \right)\) \( = {x^3} - 3{x^2} + 3x - 1 - 4{x^3} + 4x + 3{x^3} - 3 \) \(= - 3{x^2} + 7x - 4.\) LG bài 2 Phương pháp giải: Phối hợp nhiều phương pháp để phân tích đa thức thành nhân tử. Lời giải chi tiết: a) \({x^2} - {y^2} - 3x + 3y \) \(= \left( {{x^2} - {y^2}} \right) - 3\left( {x - y} \right)\) \(= \left( {x - y} \right)\left( {x + y - 3} \right).\) b) \({\left( {b - a} \right)^2} + \left( {a - b} \right)\left( {3a - 2b} \right) \)\(- {a^2} + {b^2}\) \(={\left( {a - b} \right)^2} + \left( {a - b} \right)\left( {3a - 2b} \right) \)\(- \left( {{a^2} - {b^2}} \right)\) \(=\left( {a - b} \right)\left( {a - b + 3a - 2b - a - b} \right) \) \(= \left( {a - b} \right)\left( {3a - 4b} \right).\) LG bài 3 Phương pháp giải: Biến đổi về dạng \(A\left( x \right).B\left( x \right) = 0 \)\(\Rightarrow A\left( x \right) = 0\) hoặc \(B(x)=0\) Lời giải chi tiết: Ta có: \({\left( {2x - 1} \right)^2} - {\left( {3x + 4} \right)^2} =0\) \(\Rightarrow \left( {2x - 1 + 3x + 4} \right)\left( {2x - 1 - 3x - 4} \right)=0\) \(\Rightarrow \left( {5x + 3} \right)\left( { - x - 5} \right)=0\) \(\Rightarrow 5x + 3 = 0\) hoặc \(-x-5 = 0\) \( \Rightarrow x = - {3 \over 5}\) hoặc \(x = - 5.\) LG bài 4 Phương pháp giải: Đặt phép tính theo hàng dọc và cho phần dư bằng 2 để tìm m. Lời giải chi tiết:
Từ phép chia trên ta thấy A(x) chia cho B(x) có dư bằng \(m-5\) Theo đề bài, ta có: \(m - 5 = 2 \Rightarrow m = 7.\) LG bài 5 Phương pháp giải: Sử dụng: \(m - {\left( {x - a} \right)^2} \le m\) với mọi \(x\) Lời giải chi tiết: Ta có: \(P(x) = - {x^2} + 2x + 5.\) \(= - {x^2} + 2x - 1 + 6 \) \(= 6 - \left( {{x^2} - 2x + 1} \right)\) \(= 6 - {\left( {x - 1} \right)^2} \le 6\) vì \({\left( {x - 1} \right)^2} \ge 0,\) với mọi x. Vậy giá trị lớn nhất của P(x) bằng 6. Dấu “=” xảy ra khi \(x - 1 = 0\) hay \(x = 1.\) Loigiaihay.com
|














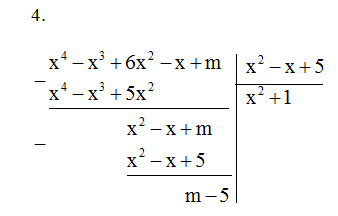






Danh sách bình luận