Đề kiểm tra 15 phút - Đề số 5 - Bài 5 - Chương 3 - Hình học 9

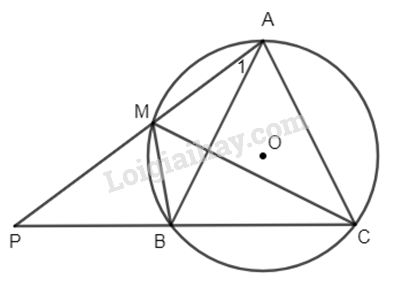
Đề bài

Tam giác ABC cân tại A nội tiếp trong đường tròn (O). Lấy M thuộc cung nhỏ AB. Gọi P là giao điểm của AM với CB.

a) Chứng minh : \(\widehat {APC} = \widehat {ACM}.\)

b) Chứng minh \(∆AMB\) và \(∆ABP\) đồng dạng.

Lời giải chi tiết

a) \(\widehat {APC} = \dfrac{{sd\overparen{AC} -sd\overparen{MB}} }{ 2}\) ( góc có đỉnh bên ngoài đường tròn)

\(\widehat {ACM} = \dfrac{{sd\overparen{AM}} }{ 2} = \dfrac{{sd\overparen{AB} - sd\overparen{MB}}}{ 2}\) ( góc nội tiếp)

Mà \(\overparen{AB} = \overparen{AC}\) (gt) \(\Rightarrow \widehat {APC} = \widehat {ACM}.\)

b) \(∆AMB\) và \(∆ABP\) có

+) \(\widehat {{A_1}}\) chung,

+) \(\widehat {MBA} = \widehat P\) ( cùng bằng \(\widehat {ACM}\) )

Vậy \(∆AMB\) và \(∆ABP\) đồng dạng (g.g).

 Loigiaihay.com