Đề kiểm tra 15 phút - Đề số 5 - Bài 10 - Chương 3 - Hình học 9

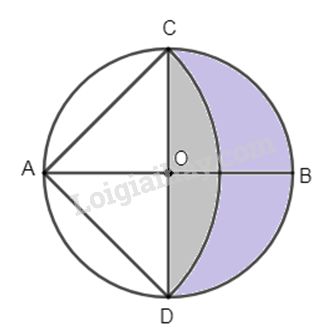
Đề bài

Cho hình tròn (O; R) hai đường kính AB và CD vuông góc với nhau. Dựng cung tròn tâm A bán kính AC. Tính diện tích hình quạt ACD và hình “ trăng khuyết” ( tô đậm).

Lời giải chi tiết

Ta có ∆AOC vuông cân có cạnh R 

\(\Rightarrow AC = AD = R\sqrt 2 \) và \(\widehat {CAD} = 90^\circ \) (chắn nửa đường tròn)

Do đó diện tích hình quạt ACD là :

\(\dfrac{{\pi {{\left( {R\sqrt 2 } \right)}^2}.90}}{ {360}} =\dfrac {{\pi {R^2}}}{2}\)

Lại có \({S_{ACD}} = \dfrac{1 }{ 2}R\sqrt 2 .R\sqrt 2  = {R^2}\)

Þ Diện tích hình viên phân CmD là :

\(S_{\text{quạt}}- S_{ACD}=\dfrac{{\pi {R^2}} }{ 2} - {R^2} \)\(\,=\dfrac {{{R^2}\left( {\pi  - 2} \right)} }{2}\)

Diện tích  (O; R) là πR² suy ra diện tích nửa đường tròn (O; R) là \(\dfrac{{\pi {R^2}}}{ 2}\).

Từ đó diện tích hình “ trăng khuyết” CBDm là :

\(\dfrac{{\pi {R^2}}}{ 2} -\dfrac {{{R^2}\left( {\pi  - 2} \right)} }{ 2} = {R^2}\).

Loigiaihay.com