Đề kiểm tra 15 phút - Đề số 4 - Bài 7 - Chương 3 – Hình học 7

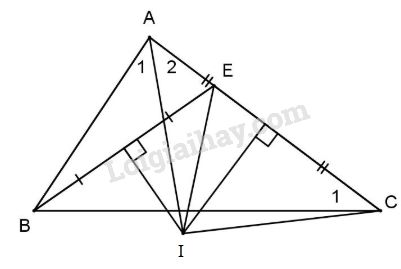
Đề bài

Cho tam giác ABC có \(AB < AC\), lấy điểm E trên cạnh CA sao cho \(CE = BA\), các đường trung trực của BE và AC cắt nhau ở I.

a) Chứng minh: \(\Delta AIB = \Delta CIE.\)

b) Chứng minh: Tia AI là tia phân giác của góc A. 

Lời giải chi tiết

a) I thuộc trung trực của đoạn BR nên \(IB = IE.\)

Tương tự ta có \(IA = IC\);  lại có \(AB = CE\) (gt).

Do đó \(\Delta AIB = \Delta CIE\) (c.g.c)

b) Vì \(IA = IC\) (cmt) nên \(\Delta AIC\) cân tại I

\( \Rightarrow {\widehat A_2} = {\widehat C_{1;}}\) 

Lại có \(\Delta AIB = \Delta CIE\)(cmt)

\( \Rightarrow {\widehat C_1} = {\widehat A_1}\) (góc tương ứng)

\( \Rightarrow {\widehat A_1} = {\widehat A_2}\) hay AI là tia phân giác của góc A.

Loigiaihay.com