Đề kiểm tra 15 phút - Đề số 6 - Bài 7 - Chương 3 – Hình học 7

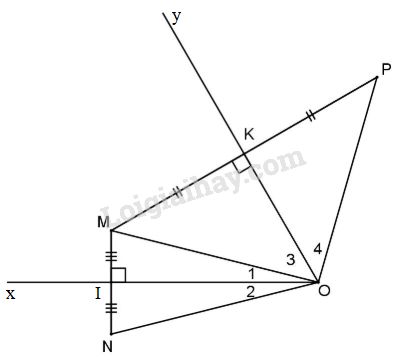
Đề bài

Cho góc \(\widehat {xOy} = {60^0}\), một điểm M nằm trong góc đó. Lấy điểm N sao cho Ox là trung trực của đoạn MN, lấy P sao cho Oy là trung trực của MP.

a) Chứng minh \(\Delta NOP\) cân.

b) Tính số đo góc \(\widehat {NOP}\).

Lời giải chi tiết

a) O thuộc trung trực của đoạn MN nên

OM = ON  (1).

Lại có O thuộc trung trực của đoạn MP nên \(MO = PO\) (2).

Từ (1) và (2) \( \Rightarrow ON = OP,\) hay \(\Delta NOP\) cân tại O.

b) (Xem hình vẽ). Dễ thấy

\(\Delta OIM = \Delta OIN\) và \(\Delta OKP = \Delta OKM\) (c.g.c)

\( \Rightarrow {\widehat O_1} = {\widehat O_2}\) và \({\widehat O_3} = {\widehat O_4}\) mà \({\widehat O_1} + {\widehat O_3} = {60^0}\)

\( \Rightarrow {\widehat O_1} + {\widehat O_2} + {\widehat O_3} + {\widehat O_4} = {120^0}.\)

Hay \(\widehat {NOP} = {120^0}\).  

Loigiaihay.com