Đề kiểm tra 15 phút - Đề số 5 - Bài 7 - Chương 3 – Hình học 7

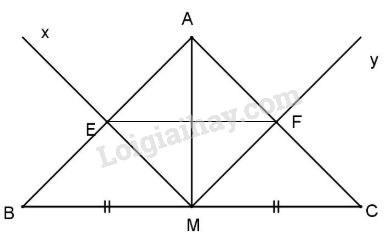
Đề bài

Cho tam giác ABC cân tại A, trung tuyến AM. Từ M vẽ đường thẳng Mx // AC cắt AB tại E,
My // AB cắt AC tại F. Chứng minh:

a) $ME = MF$;

b) AM là trung trực của EF.

Lời giải chi tiết

a) Mx // AC (gt) $\Rightarrow \widehat {{EMB}} = \widehat {C}$ (đồng vị); tương tự My // AB $\Rightarrow {\widehat {FMC}} = \widehat B$ mà $\widehat B = \widehat C$ (gt)

$\widehat B = \widehat C = {\widehat {EMB}} = {\widehat {FMC}},$ lại có MB = MC (gt)

Do đó $\Delta BME = \Delta CMF$ (g.c.g)

$\Rightarrow ME = MF$ và $BE = CF.$

b) Ta có: $AB = CA$ (gt); $BE = CF$ (cmt)

$\Rightarrow AB - BE = AC - CF$ hay $A{\rm{E}} = AF$.

Lại có $ME = MF$ (cmt). Do đó AM là đường trung trực của EF. 

Loigiaihay.com