Đề kiểm tra 15 phút - Đề số 4 - Bài 4 - Chương 2 - Hình học 9Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 4 - Chương 2 - Hình học 9 Quảng cáo
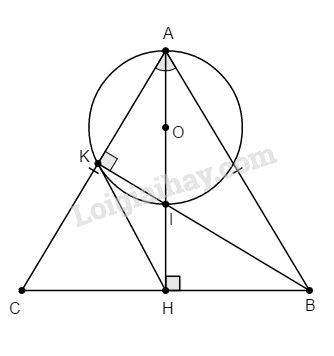
Đề bài Cho ∆ABC cân tại A, đường cao AH và BK cắt nhau tại I. Chứng minh rằng HK là tiếp tuyến của đường tròn đường kính AI. Phương pháp giải - Xem chi tiết Sử dụng: Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng đó là tiếp tuyến của đường tròn. Lời giải chi tiết
Gọi O là tâm đường tròn đường kính AI. Hiển nhiên K thuộc (O) (vì \(\widehat {AKI} = 90^\circ \) ) ∆ABC cân tại A có AH là đường cao (gt) nên AH đồng thời là đường trung tuyến \(⇒ HB = HC.\) Xét ∆BKC vuông tại K có KH là đường trung tuyến nên \(KH = BH = {{BC} \over 2}\) Do đó ∆BHK cân tại H \( \Rightarrow {\widehat B_1} = \widehat {BKH}\) (1) Lại có ∆IOK cân tại O \(\left( {OI = OK = {{AI} \over 2}} \right)\) \( \Rightarrow {\widehat I_2} = \widehat {OKI},\) mà \({\widehat I_2} = {\widehat I_1}\) (đối đỉnh) \( \Rightarrow \widehat {OKI} = {\widehat I_1}\) (2) Mặt khác ∆BHI vuông tại H (gt) nên \({\widehat B_1} + {\widehat I_1} = 90^\circ \) (3) Từ (1), (2) và (3), ta có: \(\widehat {BKH} + \widehat {OKI} = 90^\circ \) hay \(HK ⊥ OK\). Vậy HK là tiếp tuyến của đường tròn (O). Loigiaihay.com
|




















Danh sách bình luận